稳定平台是用来使被稳定对象(如瞄准具镜头、火炮炮身、雷达天线等)相对某方位保持稳定的装置。其特有的功能是隔离被稳定对象安装基座的角运动，使其不受影响。主要特征是广泛采用陀螺作为角运动敏感元件，所采用的技术手段归于惯性技术研究范畴。
　　车载卫星天线稳定系统要求车辆在移动中接收卫星信号，其核心问题是解决如何在车辆运动颠簸的情况下，保持天线波束指向不变的问题，即波束稳定问题。本系统是一种典型的两轴瞄准线稳定系统，稳定原理是在天线俯仰轴上安装两个敏感轴相互垂直的陀螺，区分敏感天线在方位和俯仰方向上相对于惯性空间的运动，并将此信号作为速度反馈，以此实现回路稳定^[1]。
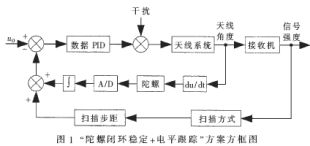
　　在跟踪过程中，由于各种误差，尤其是陀螺长期漂移的影响，随着时间的推移，天线对卫星的指向难免会偏离，造成卫星信号的丢失，即仅靠陀螺自身闭环无法满足卫星接收对跟踪精度的要求，必须建立一个良好的误差补偿机制。笔者选择“陀螺闭环稳定+电平跟踪”方案，在陀螺稳定的基础上配以电平信号跟踪环，即在跟踪的同时监控电平信号，根据信号强度辅以扫描，对天线指向给予相应的调整。方案控制方框图如图1所示。

1 各种扫描方式的比较
1.1 固定点的扫描方式
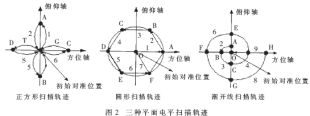
　　本系统实验过三种平面电平扫描轨迹：正方形扫描、圆形扫描和渐开线扫描，如图2所示。由于等分粗糙，步距过大，这几种扫描方式均不成功，常找错方向，得不到理想的信号最大" title="最大">最大值位置。

1.2 平面的机械圆跟踪扫描^[2]
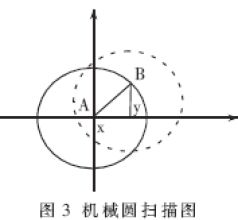
　　天线的方位和俯仰角分别按照正弦及余弦关系运动构成连续的圆轨迹，如图3所示。将圆轨迹256等分，以A为圆心扫描，采集各步信号大小。确认信号在A→B方向最大后，求出" title="求出">求出方位、俯仰分量，使圆心移到B点，继续扫描。当达到信号允许值后，中断扫描转入最大信号跟踪过程。跟踪误差大小主要取决于圆锥扫描角、直流信号的斜率及传动系统的精度。

1.3 三维空间圆锥扫描轨迹
　　已知极化轴的初始方位角" title="方位角">方位角和俯仰角，以此位置为中心线，极化轴顶点围绕它以任意半径走出圆形轨迹，在立体空间内形成一个圆锥形状，圆形轨迹为圆锥底面，如图4所示。在一个圆上等分多步，扫描采集各步信号大小，一周后根据信号最大点强度决定下一步的扫描动作，扩大扫描半径或移动极化轴继续扫描。这种扫描方式的典型特点是在三维空间形成圆锥轨迹，可以在惯性空间内找到真正信号最大点。笔者最终选择这种扫描方式。

2 圆锥扫描方式的误差补偿算法
2.1 规划圆锥扫描轨迹
　　对于方位—俯仰型两轴稳定跟踪平台，控制的本质是对方位电机和俯仰电机角度的控制。圆锥扫描算法的第一步是从空间解析几何的角度，规划极化轴在惯性空间内走出圆锥轨迹，求出圆锥底面圆上任意位置的方位角和俯仰角。
2.1.1 初始条件
　　L为极化轴长度；初始方位角为0；θ₀为初始点的俯仰角；β₀为圆锥搜索角；Z为方位轴；Y为俯仰轴。
2.1.2 假设条件
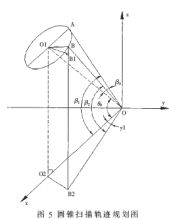
　　设b为搜索步距角，即每一步走的角度，i步后a=i×b，0≤a≤360°。搜索开始，极化轴上抬β₀，即方位角不变，俯仰角增加β₀，极化轴顶点从O₁点到A点。然后做圆锥运动，极化轴顶点轨迹是一圆周，如图5所示。扫描半径r=L×sin(β₀)，β₁=θ₀+β₀，B为圆周过程中任一点。

2.1.3 求解结果
　　俯仰角：
　　
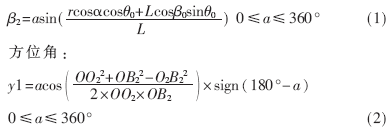
2.2 Matlab验证圆锥扫描轨迹
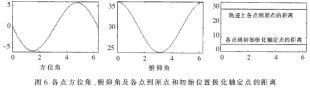
根据已知求出圆周上各点(即极化轴顶点)的方位角和俯仰角，在立体空间做出图形，如图4所示。初始俯仰角30°，方位角0°，锥角5°，每周360个点，各点方位角、俯仰角及各点到原点和初始位置极化轴定点的距离如图6所示。显然，圆锥轨迹规划正确，根据算得方位、俯仰角可以在三维空间得到圆锥轨迹。
2.3 实际系统圆锥扫描轨迹验证
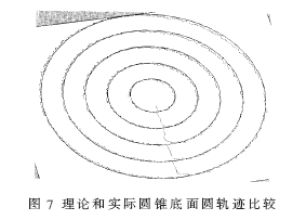
　　理论和仿真服务于实际，希望确保极化轴在惯性空间真实能走出圆锥轨迹。规划圆锥轨迹，通过运动控制器控制电机动作，位置模式保证每点位置，记录每步方位、俯仰旋转变压器数值。如图7所示为旋变后得到的轨迹与理想轨迹的比较(已在三维空间旋转)。从图形可以清楚地看出实际方位、俯仰电机所走位置与理想圆锥轨迹相差无几。

3 圆锥扫描在静止间初始对准中的应用
　　在车载卫星天线稳定系统进入移动跟踪之前，首先要求在静止间准确对准卫星，接收到良好的电视信号。由于数字罗盘自身的精度，以及方位、俯仰旋转变压器和数字罗盘的安装误差带来的影响，经过数字罗盘测得的车体姿态换算成天线的指向角往往与实际指向角存在一定的偏差。为了准确地对准卫星，使天线在初始对准角周围进行圆锥扫描，同时记录每个位置的电平电压值，从中选定信号最好的位置，然后驱动天线指向此位置。
　　静止间圆锥扫描的基本思路是：采用较大步距、较大范围的粗扫描；发现电视信号以后，马上停止锁定该位置；进行较小半径、较小范围的扫描，直到确定最佳信号位置。
4 移动跟踪中“跟踪+扫描”的控制方式
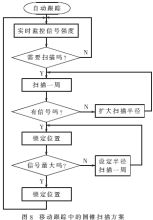
　　车载卫星天线稳定系统移动跟踪间的圆锥扫描问题集中在三个方面：(1)稳定性。速率陀螺HORIZON所能感应到的速率自身有一定的限制，这要求固定频率下扫描步距不能太大。(2)方向性。圆锥扫描要求保证得到正确的最大值方向，并且尽可能直接指向信号最强点的最优化方向。(3)递进性^[3]。当信号丢失时，扫描一周仍然没有信号，要求增大扫描半径继续扫描。扫描一周得到一个最大值方向，但不是信号最强点，要求以新位置为圆心继续扫描。
　　移动跟踪中的圆锥扫描方案如图8所示。