TMS320C54X（以下简称'C54X）是TI公司于1996年推出的新一代高性能定点DSP。该系列芯片具有很高的性能价格比、体积小、功耗低、功能强，已成为通信、计算机、消费类电子产品等领域的重要器件。数字滤器的设计是数字信号处理领域的一个重要部分。在用定点DSP器件设计数字滤波器时，一个重要的问题就是由于硬件字长精度有限，运算会出现溢出。IIR滤波器可以用较少的阶数获得很高的选择特性，所用的存储单元少、运算次数少，具经济、高效的特点。在相位要求不敏感的场合，如语音通信等，很适合用IIR滤波器；但是在有限精度的运算中，可能出现不稳定现象。因此，有必要讨论一下如何在定点的DSP芯片'C54X上实现扩展精度的IIR滤波器。
1 'C54X DSP上扩展精度乘法的实现
'C54X芯片的CP内含有2个40bit的累加器（ACC A和ACC B）、1个17×17bit乘法器以及1个40 bit加法器。这就使得该乘法器可以实现2个无符号数、2个有符号数或无符号数和有符号数的乘法。
累加器ACC A和ACC B存放从ALU或乘法器/加法器单元输出的数据，也能输出到ALU或乘法器/加法器中。累加器包括3部分（见图1）：
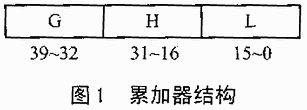
①保护位（bits 39～32），用来作为计算的前部留空（headmargin），防止在迭代运算（如自相关）中产生溢出；
②高位字（bits 31～16）;
③低位字（bits 15～0）。
'C54X芯片内部的特点，使得扩展精度计算行之有效。其中一个就是进位的处理。算术逻辑单元ALU执行大多数指令操作，如循环与移位操作都会影响进位。进位操作通过调用ST0，设置或重设状态寄存器来修改。正常操作中，为了使累加器不至于装入饱和值，溢出模式应该设置为OVM=0。
'C54x内部的2条数据总线（CB和DB）允许一些指令在其周期内操作32bit操作码。长字节操作指令和双精度加减指令使用了32bit操作数，能够高效地实现多精度算术操作。硬件乘法器能够对有符号和无符号数进行操作，可以乘2个有符号数和2个无符号数。这样，32bit的乘法就能有地进行。
2个32bit整数的乘法，需要有1次乘法、3次乘法/累加和2次移位运算。其结果是1个64bit的整数，实现程序如下（假设事先已设好SXM=1，OVM=0）。
数据存储如下：H1，L1存32bit操作数；H2，L2存32bit操作数；R3，R2，R1，R0存64bit乘积
STM #L1，AR1 ；AR2→L1
STM #L2，AR3 ；AR3→L2
LD *AR2，T ；T=L1
MPYU *AR3+，A ；A=L1*L2
STL A，@R0 ；保存R0
LD A，-16，A ；A=A>>16
MACSU *AR2+，*AR3-，A；A=L1*L2>>16+L1*H2+H1*L2
MACSU *AR3+，*AR2，A；A=L1*L2>>
；16+L1*H2+H1*L2+H1*L2
STL A，@R1 ；保存R1
LD A，-16，A ；A=A>>16
MAC *AR2，*AR3,A ;A=（L1*L2+H1*H2）>>16+H1*H2
STL A，@R2 ；保存R2
STH A，@R3 ；保存R3
2 IIR滤波器的基本原理及编程实现
N级IIR滤波器的脉冲传递数表达式为
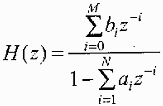
它的差分方程表达式为
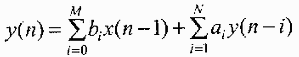
由上式可见，y(n)由2部分构成；第1部分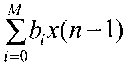
是一个对x(n)的M节延时结构。每节延时后加权相加，也就是一个横向结构网络。第2部分
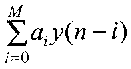也是一个N节延时的横向网络结构，不过它是对y(n)延时，因此也是个反馈网络。
数字滤波器运算结构的不同，将会影响系统运算的精度、误差、速度和经济性等性能指标。在一般情况下，都要求使用尽可能少的常数乘法器和延迟器来实现系统，并要求运算误差尽可能小。然而，这些要求有时是互相矛盾的，例如，为了获得个有较小运算误差的结构，使用的乘法器和延迟器的数目往往并不是最少的。IIR滤波器有以下几种基本网络结构：直接I型、直接II型、级联型和并联型。各种结构都有其优缺点。鉴于级联型常用于均衡器中，而且优点比较突出，所以，以级联型为便详细介绍其算法实现。
IIR滤波器在采用级联实现的，将传递函数分解为二阶传递函数的乘积，即
H(z)=H1(Z)H2(Z)…HM(Z)
每一级的子滤波器Hk(z)常取以下的形式：
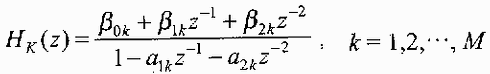
一般级联实现都采用直接II型结构作为子滤波器的网络结构。使用直接II型的子滤波器的网络结构如图2所示。
二级级联IIR滤波器的主要实现程序如下：
；***已初始化了PMST=FFA0H,ST1=2300H,
;SWWSR=0,OVM=1，FRCT=1，SXM=1
STM #X，AR1
STM #Y，AR2
STM #d,AR3 ;AR3:d(n),d(n-1),d(n-2)
RPT A,#5 ;初始化d(n),d(n-1),d(n-2)=0
STL A，*AR3+
STM #2，AR0 ；初始化Arn是地址偏移量为常数
INLOOP：
STM #d+5,AR3 ;AR3：d(n),d(n-1),d(n-2)
STM #table,AR4 ;AR4:IIR的系数A2，A1，B2，B1，B0
PORTR 100H，*AR1 ；从端口读入数据
LD *AR1，7，A
STM #N-1，BRC ；计算IIR的节数N
RPT ELOOP
LOOP：
********反馈通道**************
MAC *AR4+，*AR3-，A ；input+d(n-2)*A2
MAC *AR4,*AR3,A-;input+d(n-2)*A2+d(n-1)*A1
MAC *AR4+,*AR3-,A
STH A,*AR3+0;d(n)=input+d(n-2)*A2+d(n-1)*A1
********前向通道*************
MPY *AR4+，*AR3-，A ；d(n-2)*B2
MAC *AR4+,*AR3,A;d(n-2)*B2+d(n-1)*B1
DELAY *AR3- ;d(n-2)=d(n-1)
MAC *AR4+,*AR3,A;d(n-2)*B2+d(n-1)*B1+d(n)*B0
DELAY *AR3-;d(n-1)=d(n)
ELOOP:
STH A,*AR2;output=d(n-2)*B2+d(n-1)*B1+d(n)*B0
PORTW *AR2,200h ；将结果写入文件中
BINLOOP ；计算下一个输出
3 均衡器用扩展精度IIR滤波器的编程实现
IIR滤波器的一个典型应用，就是用作均衡器。在级联型的结构中，可以用极点和零点配对的方法，把共轭的零、极点或相近的零、极点组合在一个二阶滤波器中，这对于降低有限字长系数的敏感程度十分有效。另外，交换级联次序也是减少有限字长效应的一个行之有效的方法。本文给出用二阶级联扩展精度IIR滤波器实现时域均衡器的程序。
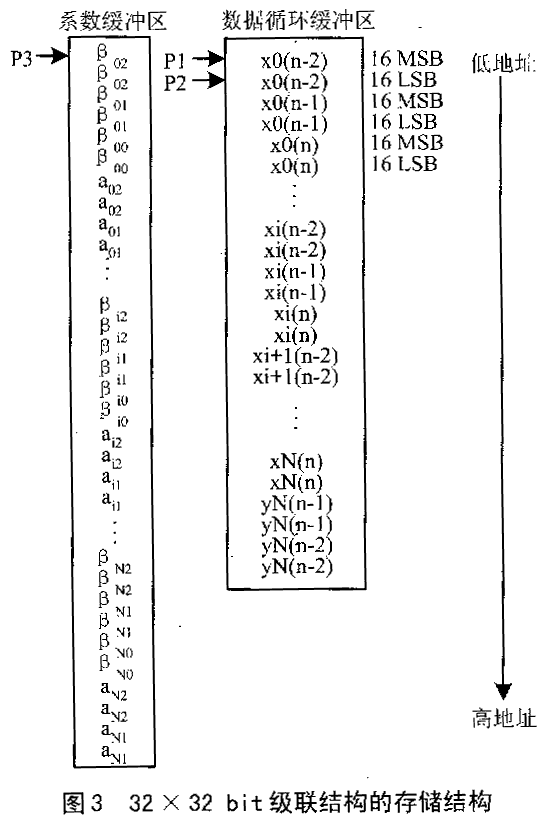
本程序中使用了一个循环缓冲区用来存放数据，要求计算出的系数均循在-12～12dB。为了防止溢出，使最大增益为4，通常要结果右移2bit（相当于结果除4）。这样就范围变成了-24～0dB（因为20log（1/4）=-12dB）。每个滤波器的通带频率集中在某个比较感兴趣的频率段。滤波器系数的绝对值可能比1大。当用Q15格式表示时，必须除2的整次幂来满足限定的范围[-1,1～2 -15]。所以系数在存入存储器之前要右移，那么与此对应的在存入每个滤波器输出系数时要左移。32×32bit直接II型的级联结构运算量如下：周期数为29，RAM为16字。寄存器数为6。
系数缓冲区和数据缓冲区的长度不同，且仅数据缓冲区是循环缓冲。32×32bit级联结构的存储器结构如图3所示。