在科学和工程的许多领域中，滤波在动态系统的状态和参数估计中得到了广泛的应用。当一个系统的模型和参数完全已知时，卡尔曼滤波的各种形式及其推广式是能够获得最小均方误差的普遍方法。但当这些条件不能满足时，例如，当一个系统的结构和部分参数未知时，或者一个基本物理系统在不同的时间段具有不同的参数/结构描述时，自适应多模划分滤波器(MMPF)被最为广泛地应用。自适应多模划分滤波器是为了自适应估计和控制的需要而产生的一系列多模划分方法之一。
　　当建立的模型在关心的范围内保持不变时，作为结果的MMPF是固定结构的。这种滤波器在多种实际问题中比较实用。然而，在很多情况下建立的模型不能达到最优化设计。例如，很多实际问题的参数是连续的，而不是假设的离散的。在这些情况下，变结构的MMPF得到了应用，这时假定的模型是时变的。
　　本文通过使用合理设计的遗传算法来实现MMPF，它能够动态、实时地改变结构以适应所建立的模型。通过仿真实验，证明了此算法比固定结构MMPF的执行效果更优越。
1 自适应估计的多模划分方法
　　MMPF的框图如图1所示。

　　根据上面的" title="面的">面的描述，一个MMPF的设计主要由以下几部分组成：
　　(1)模型集设计：必须设计由多个模型组成的模型集。
　　(2)滤波器选择：即选择基本的滤波器类型，尽管通常选用卡尔曼滤波器作为基本滤波器，但实际上也可选择任何其它类型的滤波器，只要能满足MMPF要求的质量即可。
　　(3)估计融合：产生总体估计。
　　(4)滤波器的重新初始化：可以根据每个滤波器前一步的估计和误差协方差，或者根据整个MMPF前一步的估计及误差协方差进行初始化。
　　在实际工程应用中，这种自适应多模划分滤波器(MMPF)存在下述几个方面的问题：
　　(1)明显地，多模型估计器对于能够用变结构和参数描述的问题具有较好的效果，但是要求所有可能的系统模型和参数值都是已知的，而且数量是有限的。
　　(2)不考虑所采用的方法，在设计中还会遇到一个严重的问题：如何选取有限的参数子集的基数。在这个问题上，要考虑以下两点：
　　·MMPF估计的质量通常随着采用的滤波器数量的增多而提高。因此，基数小的子集会导致估计的质量较差。
　　·MMPF的计算量与采用的滤波器数量是成比例的。因此，基数大的子集会导致计算量很大，甚至使MMPF不能实时执行。
　　(3)很明显，自适应估计器能够识别未知的参数。当真实的参数值在假定的采样空间内时，估计器会收敛到这个值。当真实的参数值不在假定的采样空间内时，估计器会收敛于采样空间中离真值最近的值。在这种情况下，对未知参数的准确识别是办不到的。
　　变结构的MMPF能够修正传统的固定结构MMPF的上述缺点。
2 基于遗传算法的变结构MMPF
　　本文仅考虑实际感兴趣的离散时间和离散参数的情况。然而，这一讨论也同样适合连续参数的情况。这里介绍了两种算法形式，最终将会看到，每种形式适合于不同的用途。
　　第一种算法形式更适合于模型的设计，它使用s个矢量(串)，表示为vⁱ(i=1,…，s)，每一矢量包含m个参数θ的可能取值。初始值从Ω_θ空间随机选取，Ω_θ空间假设为离散的。如果不是这种情况，在选取θ值前要加一离散化的过程。对每一矢量应用MMPF进行m次采样，计算包含在矢量中的所有可能后验概率值。每一矢量的合适的值定义为θ，具有最大后验概率值时，也就是F((vⁱ)=[θ₁ⁱ，θ₂ⁱ,…,θ_mⁱ])=max_j=1,…,m p(θ_jⁱ|k)，i=1,2,…，s,其中θ_jⁱ表示第i个矢量的第j个分量。为了下一代的进化，采用遗传操作的选择、交叉和异化。新一代的串(矢量)重复上一代的过程，整个过程不断重复直到所设定的代为止，或者直到适应函数(fitness function)等于1，也就是概率的最大值。算法示意图如图2所示。

　　对于这种算法，说明如下：
　　(1)如上所述，算法的这种形式更适合于模型(组)的设计。事实上，当算法终止时，最后一代种群的最佳染色体组是最优模型，因为它具有最大的后验概率，即至少有一个基本成分等于参数的真实值。
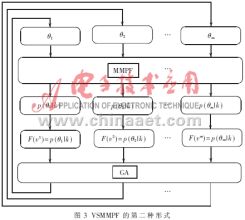
　　(2)为了利用算法的这种形式，需要知道许多模拟过程的测量值。这就意味着这种算法必须在脱机后运行，或是以低于测量的速度运行。算法的第二种形式更适合于最优化的估计，它使用m个矢量(串)，每一个都是一个未知参数θ的可能取值，这些值表示为θ_i，i=1,2,…，m。种群的初始取值是利用在Ω_θ空间的随机均匀采样。其次，通过一次采样，MMPF用来为每一个θ_i产生一个后验概率p(θ_i|k)，将其作为相应于θ_i的适应值。下一代再次通过遗传算法的选择、交叉和异化来产生。这样的过程按需要利用GA持续进行。最后一代构成了一组MMPF的新模型。算法示意图见图3。
　　(3)正如上面所述，算法的第二种形式更适合于最优估计。事实上，当GA收敛时，真正的参数值是MMPF模型的一项，认为它已经达到了适应的唯一最大值。
　　(4)对基本滤波器重新初始化时，会遇到一个细微但很重要的问题：在MMPF每一次迭代时，模型可能是不同的，也就意味着基本滤波器的设置将会不同。那么如何重新初始化这些滤波器呢？尽管有许多可行的方法，笔者还是选择用当前MMPF的最大后验概率(MAP)估计与其相关联的误差协方差来重新初始化这些滤波器。
　　(5)在算法的描述中，并没有提到在参数编码、GA的初始化及选择、交叉和异化操作等方面的选择问题。这是因为通用的GA方法在这里都可应用。在标量模型的情况下，编码可以是实数或二元的。在多变量模型的情况下，可采用实数编码。初始化可以均匀实现或是使用有偏的初始化。选择控制器可以采用转轮形式。对于交叉控制器，可以选择均衡交叉控制器、单向交叉控制器、双向交叉控制器、奇偶交叉控制器、算术交叉控制器或混合交叉控制器。异化可以通过交换控制器或高斯异化控制器实现。这一结论对两种算法的实现方式都适用。
3 仿真结果
　　为了证明该算法的适用性和性能，完成了几个仿真实例：一个使用标量的系统模型、一个使用多变量的系统模型和使用ARMA模型的状态空间表示。
　　仿真实例1——标量模型，使用由如下方程描述的标量模型：

　　x(k+1)=0.9x(k)+w(k)
　　z(k)=Hx(k)+v(k)
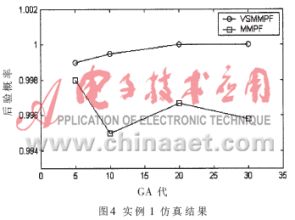
　　未知参数是标量矩阵（常数）H的值，其范围在[0,1]内。初始状态为x(0)~N(0.1,1)，Q=0.4,R=0.1。为设计滤波器，为H（在[0,1]内）假定M个可能的值，并设每一个可能值Hi（i=1,2,...,M）的先验概率为p(H_i)=1/M。实验结果如图4所示，其中固定结构的MMPF（真实的参数值不在模型中）和第一种方式的VSMMPF的后验概率已经示出。显然，VSMMPF在GA的第20代时就已经得到了真实参数值。

　　仿真实例2——多变量模型，使用如下方程描述的多变量模型：
　　
　　其中，3×5的矩阵H的测量值未知，只是已知H[i，j]∈[0，-30]，i=1,2,3，j=1,...,5，并且
　　
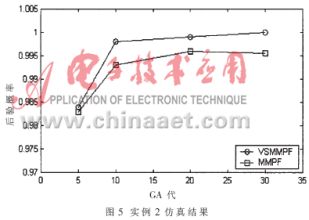
　　实验结果如图5所示，画出了固定结构MMPF和第一种方式的VSMMPF的后验概率。