锁相环是一种能够跟踪输入信号相位的闭环自动控制系统，广泛应用于信号处理、时钟同步、倍频、频率综合等领域。它根据输入信号和反馈信号的相位差来调整压控振荡器的输出频率，最终达到输入信号频率和输出信号频率相等，输入信号和输出信号保持恒定的相位差。
    传统的PI控制器可以消除稳态误差，保证锁定精度，但是对阻尼有不利影响。在PI控制器中引入微分项可以改善响应速度和阻尼，保证了锁定时间，但不能减少稳态误差，因此本文提出积分分离PID控制，能够大大改善响应时间和阻尼并减少稳态误差，从而保证了锁相精度和锁相时间。
1 电路结构与工作原理
1.1 全数字锁相环电路结构
    快速全数字锁相环的系统框图如图1所示。

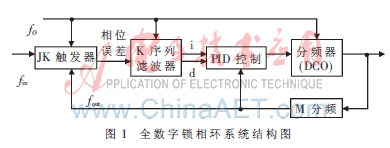
    鉴相器采用JK触发器，该鉴相器结构简单，鉴相范围为±π，能够满足一般工程的需要。由于鉴相器输出的是二值高低脉冲，后需接数字滤波器来平滑其中的起伏，消除噪声和干扰脉冲的影响。一般数字序列滤波器有两种：N先于M序列滤波器和随机徘徊滤波器，数字滤波器不是环路滤波器，它是无惰性的，加在环路中不影响环路的阶数，仅起到滤噪抗干扰的作用。本文采用随机徘徊滤波器。环路滤波器采用PID控制器，能够很好地控制环路相位校正的速度和精度，相对于文献[1]的PI控制器具有更好的特性。数字压控振荡器采用可变模的分频器。M分频器对输出信号进行分频，以使环路得到相应的倍频信号。
1.2 电路工作原理
    鉴相器比较输入信号和输出信号的相位差，产生一误差高低电平脉冲序列pha。该脉冲的宽度和输入、输出信号的相位误差是成比例的。K序列滤波器对相位误差信号进行量化，又可以消除输入信号噪声和干扰脉冲的影响。当pha为高电平时，K序列滤波器对fO进行加计数，当计数器溢出时，一方面向环路滤波器产生一加脉冲i，同时对计数器进行复位，重新计数。相反，当pha为低电平时，K序列滤波器对fO进行减计数，当计数器减为零时，一方面向环路滤波器产生一减脉冲d，同时对计数器进行复位，重新计数。在一个pha周期内，K序列滤波器产生加减脉冲的综合值，表征了输入信号和输出信号相位误差的大小。由于干扰和噪声的影响是随机的，此时K计数器产生的加减脉冲的概率相等，因此环路具有较强的抗干扰能力。环路滤波器采用了PID控制，所以，数字压控振荡器输出的信号经M分频后，反馈给环路滤波器作为采样信号。环路滤波器在其上升沿对一个pha周期内由K计数器产生的加减脉冲个数进行计数综合、PID计算、并把计数值输出给压控振荡器作为分频因子和寄存器清零操作。在控制过程中，由于把压控振荡器输出的信号M分频后的信号作为环路滤波器的采样信号，因此保证了采样周期和输出信号fout的周期是同步的，这样既保证了逐周波控制，也保证了在压控振荡器的计数开始时赋予其寄存器新的分频计数值。
2 系统结构性能分析
2.1 数学模型分析
    图2是图1中全数字锁相环的数学模型。

 

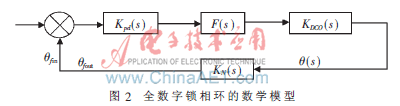
    由文献[1]中对PI控制器及系统闭环响应的分析，可以得到PI控制锁相环能够使控制满足超调量、调节时间和零稳态误差以及自然谐振频率与输入信号的频率成正比的优点。然而需要更快的响应速度，且又不增加超调量，则应在控制器中增加微分项，即PID控制。在传统的PI控制中，由于积分项的存在，虽然可以消除静差、提高精度。但在过程的启动、结束或大幅度增减设定值时，短时间内系统会输出很大的偏差，会造成PI运算的积分积累，最终引起系统较大超调，甚至引起系统的振荡。因此本文采用了积分分离的PID控制算法，既保持了积分作用，又减少了超调量，使控制性能有了较大的改善。具体实现如下：

    积分分离PID算法的仿真图如图3所示。

2.2 环路线性分析
    当锁相环在锁定点附近波动时，计数值N的变化较小，假设此时环路为二阶环，压控振荡器的传递函数为：
  
  

    由式(7)、(8)可以看出，只要得到K序列滤波器的计数值k、积分系数 ki、比例系数 kp，就可以得到环路的谐振频率和阻尼系数，反之依然。此外观察自然谐振频率可得它与输入信号的频率成正比，这意味着锁相环的跟踪速度和输入信号的频率成正比。
    PID参数工程整定的一般步骤：
    (1)只加入比例控制环节，慢慢增加kp使系统微微振荡起来。
    (2)加入微分控制环节，慢慢减小kd，这相当于增大系统的阻尼，使系统平稳下来。
    (3)系统平稳下来后，再增加kp使系统微微振荡起来，然后再减小kd使系统平稳下来。如此反复下去，直到kp和kd都不能变化时为止。
    (4)把kp的值适当减小一点，加入积分控制环节，慢慢增加ki的值，直到稳态误差在可接受的范围内。
    (5)为了使系统更可靠和稳定，保证鲁棒性。最后还要把kp、kd、ki的值都适当减小，再根据经验做一些相应的调整。
3 系统仿真分析
3.1 仿真结果
    本设计使用VHDL语言进行设计，以Quartus软件为设计平台，用CycloneII EP2C35F484C8 器件完成设计。
    本设计中参数均用整数，选择为ki=2，kp=2，kd=4，K序列滤波器的模值为36，M分频比为1在相位阶跃为180的情况下的系统仿真图如图4。

3.2 结果分析
    经过反复调整系统的参数K值，选定一个较好的K值作为序列滤波器的模值，选定ki=2、kp=2、kd=4作为PID的积分系数、比例系数和微分系数。从仿真图上可以看出，该设计结构能够达到锁定状态，且锁定时间有所减少，达到了预期的效果。
    本文提出了一种新型的环路滤波器，采用积分分离的PID控制器作为环路滤波器，有效地减少了锁定时间，提高了锁定精度。该锁相环具有很强的通用性，并且电路参数配置方便、设计简单、集成度高。理论分析、仿真和实验结果都表明该全数字锁相环性能良好。使用FPGA实现，占用资源较少，容易做成片上系统SoC。
参考文献
[1] 李亚斌，彭咏龙，李和明.自采样比例积分控制全数字锁相环的性能分析和实现[J].中国电机工程学报，2005(9).
[2] ROLAND E.Phase-Locked Loop design,  simulation,  and  application[M].北京：清华大学出版社，2003.
[3] 张厥盛，郑继禹，万心平.锁相技术[M].陕西西安：西安电子科技大学出版社,1994.
[4] 陶永华，尹怡欣，葛芦生.新型PID控制及应用[M].机械工业出版社，2000.
[5] 周润景，图雅，张丽敏.基于Quartus ii 的FPGA/CPLD数字系统实例[M].北京：电子工业出版社，2008.
[6] 侯卫民，蒋景红，张骋，等.基于FPGA的数字锁相环的研究与实现[J].微计算机应用，2008(8).