乘法器被广泛应用于各种数字电路系统中，如DSP、数字图像处理等系统。随着便携电予设备的普及，系统的集成度越来越高，这也对产品的功耗及芯片的散热提出了更高的要求。本文提出了一种新的编码算法，通过这种算法实现的乘法器可以进一步降低功耗，从而降低整个电子系统的功耗。

1 乘法器结构
    本文介绍的24×24位乘法器的基本结构如图1所示。其中，“降低乘数中‘1’的数量”实现对乘数y的编码，以降低乘数y中“1”的数量，这可以在“部分积产生电路”中降低部分积的数量，“部分积产生电路”产生的部分积在“改进后的阵列加法器”和“超前进位加法器”中相加，最后得到乘积z。

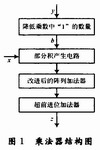
2 降低部分积数量的编码算法
    设x，y是被乘数和乘数，它们分别用24位二进制数表示，最高位是符号位，z是乘积，用47位二进制表示，最高位是符号位，“1”表示负数，“0”表示正数。则它们的关系可以用下式表示：
                     
   
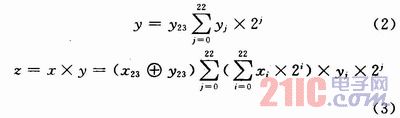
    式中：xi，yi分别是x，y的权位。如果按式(3)进行乘法计算，需要将与所有的yi相乘，产生23行部分积，然后再将其相加，即使yi=0，也要进行上述运算，这样就势必增加乘法器的功耗和延时，因此，在下面将会对全加器和半加器进行改进，使仅与yi=1相乘，从而避免与yi=0相乘。首先介绍降低乘数y中“1”的数量的编码算法。用一个事例说明本文介绍的算法的优越性。设m1，m2分别是乘数和被乘数，且令m1=01110111，如果用m2与m1中的每一位相乘，则会产生6个m2和2个“0”列，如果按照Sanjiv Kumar Mangal和 R． M．   Patrikar所建议的方法，则：
    01110111(m1)=10001000(n1)-00010001(n2)    (4)
    将m2分别与n1和n2相乘，再将它们的乘积相减即得乘积结果。但是，在这一过程中，一共产生4个m2。如果按照本文所建议的方法，会进一步降低m2的数量，即：
    01110111(m1)=10000000(n1)-00001001(n2)    (5)
    由式(5)可以看出，n1和n2中共有3个“1”，因此，可以进一步降低部分积的数量。当乘数的位数较大时，本文提出的算法优越性更大。具体编码流程如图2所示。

3 部分积的产生及相加
    在数字电路中，功耗主要由3部分构成，即：
   
    式中：Pdynamic是动态功耗；Pshort是短路功耗；Pleakage是漏电流功耗。当CMOs的输入信号发生翻转时，会形成一条从电源到地的电流Id对负载电容进行充电，从而产生Pdynamic。一般情况下，Pdynamic占系统功耗的70 ％～90％。因此，有效地降低Pdynamic也就降低了电路功耗。
    为了降低CMOS输入信号的翻转活动率，本文对部分积相加过程中用到的全加器和半加器进行了必要的改进，从而避免当乘数y的某一位是“0”时输入信号的翻转，本文的全加器和半加器的结构如图3所示。

    图3中，xi+1，xi分别是被乘数的某一位，yi是乘数的某一位，ci，ci+1，co是加法器的进位输出信号，si是加法器的和。
    从图1中可以看到，y经过编码以后得到两个数b和c，其中，b是24位二进制数，c是21位二进制数。由式(5)可得到下式：
    z=x×b-x×c (7)
    为了降低乘法器的延迟，将b和c分别分成三部分(即 b[23：16]，b[15：8]，b[7：0]，c[20：16]，c[15：8]和c[7：O])，x分别与这6个数相乘可以得到6组部分积，每一组部分积分别采用图4所示的阵列加法器相加，即得到6个部分积和(sb2，sb1，sb0，sc2，sc1，sc0)。图4中的HA，FA0，FA1分别对应图3中的HA，FA0，FA1；ADD是FA0改进前的全加器。则sb2，sb1和sb0错位相加可以得到x×b的积sb，sc2，sc1和sc0错位相加可以得到x×c的积sc，所有这些错位相加以及得到最后的乘积z都是通过超前进位加法器来实现的。

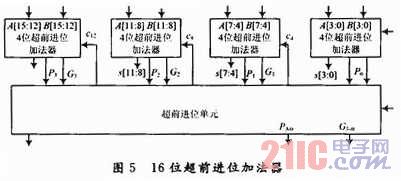
    在由sb，sc得到z的两个47位二进制数相加过程中，用到了3个如图5所示的16位二进制加法器，它包括4个4位超前进位加法器和1个超前进位单元(其中，Pi为进位传播函数，Gi为进位产生函数)。错位相加过程中用到的超前进位加法器与图5中16位超前进位加法器结构类似，在此不再阐述。

4 仿真与功耗测试结果
    图6所示是乘法器的功能仿真波形图，可以看到，本文所介绍的乘法器的功能是正确的。

    本文所介绍的乘法器是由VerilogHDL编程实现的，因此，在Altera的FPGA芯片EP2C70F896C中进行功耗测试，功耗测试过程中环境变量设置如表1所示。

    对功耗的测试时间是1μS。在测试时间内，给乘法器加入不同的测试激励，观察功耗变化情况，为了说明本文提出的算法的优越性，同时也测试了由现有的两种编码算法所实现的乘法器，测试结果分别如表2～表4所示(其中，whole表示表格前部的测试激励在测试时间内依次输入)。

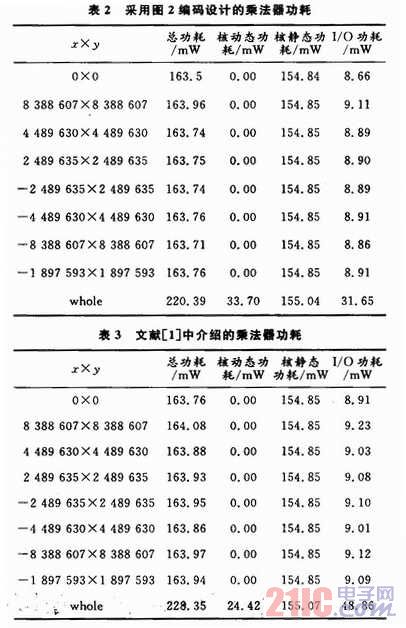
    从图6中可以看出，在测试时间内，当测试激励保持不变时，FPGA芯片的核动态功耗0．00 mW，总功耗比较小，用三种编码算法实现的乘法器功耗差别不大，说明在只进行一次乘法运算时，COMS的输入信号基本没有翻转；当输入激励在测试时间内变化，即在whole状态时，三个乘法器都有动态功耗，说明CMOS的输入信号随着电路输入信号的变化而翻转。本文介绍的乘法器的总功耗比文献介绍的算法降低了3．5％，比基于Booth-Wallace Tree的乘法器的功耗降低了8．4％。

5 结语
    本文介绍了一种新的编码方法，它相对于文献中的编码可以进一步降低乘数中“1”的数量，从而进一步降低了乘法器的功耗；另外，还对传统的全加器和半加器进行了改进，从而降低CMOS输入信号的翻转率，从而降低了功耗。并且，通过在Altera公司的FPGA芯片EP2C70F896C中进行功耗测试，可以看出本文介绍的乘法器的功耗比文献中介绍的乘法器的功耗降低了3．5％，比基于Booth-Wallace Tree的乘法器的功耗降低了8．4％。