基于畸变校正的双目立体摄像机线性标定-AET-电子技术应用

基于畸变校正的双目立体摄像机线性标定

来源:电子技术应用2011年第1期

崔莉娟, 朱洪俊, 王金鹏

西南科技大学制造科学与工程学院, 四川绵阳621010

摘要： 利用透视变换原理建立双目立体摄像机数学模型，全面考虑了镜头的径向畸变和切向畸变，提出一种线性求解摄像机参数的标定方法，改变了以往的摄像机标定依赖于非线性优化的缺点,避免了非线性优化的不稳定性。该标定方法在单摄像机模型的基础上，加入对双摄像机相对位置的确定,通过成像过程中坐标系之间的转换，较好地实现了双目立体摄像测量系统的标定。

关键词： 摄像机标定双目立体摄像镜头畸变

中图分类号： TP391.41
文献标识码: A
文章编号： 0258-7998(2011)01-0084-03

Study on linear calibration of binocular stereo cameras based on distortion revision

Cui Lijuan, Zhu Hongjun, Wang Jinpeng

College of Manufacturing Science and Engineering, Southwest University of Science and Technology, Mianyang 621010, China

Abstract： This article sets a mathematical model of binocular stereo cameras using the perspective projection transformation theory, it takes a comprehensive consideration of the radial and tangential distortion of the camera, put forward a linear approach of calibration. This method has changed the disadvantage that camera calibration have to depend on the tradition nonlinear optimization, and avoid obtaining unstable solution under common experiment conditions. On the basis of single camera calibration, this calibration add the relative orientation and location between the two cameras into the model, by the transition between the coordinate systems in the imaging process, it realizes the calibration of the binocular stereo vision measurement system.

Key words : camera calibration; binocular stereo vision; lens distortion

    摄像机标定是为了确定摄像机的位置、属性参数和建立成像模型，以确定空间坐标系中物点与它所在图像平面上像点之间的对应关系[1-2]。国内外学者对摄像机标定做了大量的研究，提出了许多不同的标定方法[3-4]。鲁新国等[5]提出了线性摄像机标定技术，其计算简单，精度较高，但只考虑了径向畸变，当切向畸变较大时不适用。陈利红等[6]提出了摄像机标定与修正的简单方法，考虑了镜头的径向畸变和切向畸变，利用两步法，计算精度较高，但是方法复杂，需要优化算法，不易实现。
     目前，线性摄像机标定技术的研究集中在如何有效地、合理地确定非线性畸变校正模型的参数上[7]。本文采用的算法全面考虑了径向畸变和切向畸变，通过建立和求解超定线性方程组计算出畸变系数，然后利用约束方程求解线形方程组，来确定摄像机外部参数和内部参数。该算法全部过程采用线性方法求解全部参数，不仅简单快捷，而且没有非线性算法中可能存在的不稳定性，实用性较强。
1 双目摄像机标定模型与原理
1.1 摄像机标定模型
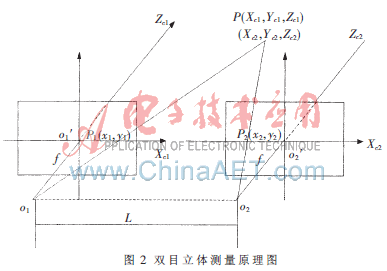
   如图1所示，计算机图像坐标系o0uv,坐标系原点在图像左上角，以像素为单位。图像平面坐标系o1xy，原点位于摄像机光轴与图像平面坐标系的交点，利用透视变换原理可知，该原点与图像平面的几何中心重合，x轴平行于u轴，y轴平行于v轴。o1点在坐标系o0uv中的坐标为o1(u0,v0)。摄像机坐标系是以摄像机光心o为原点的坐标系，记为XcYcZc。oo1之间的距离为摄像机的焦距f。P点为空间点，在摄像机坐标系中的坐标为(XcYcZc)。P点与图像坐标系的交点为P′，P′点在小孔摄像机模型下的图像坐标为(xu,yu)，由透镜畸变引起的实际图像坐标为(xd,yd)。

摄像机标定包括四个坐标系之间的转换：即计算机图像坐标系、图像平面坐标系、摄像机坐标系和基准坐标系(世界坐标系)。

(1)计算机图像坐标系与实际图像坐标系之间的转换：

(2)将空间坐标点的实际空间坐标值与恢复后的三维空间坐标值进行比较，利用绝对误差来表示实验精度，如表1所示（部分实验数据）。

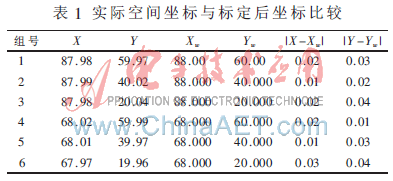
Xw、Yw表示真实三维坐标，X、Y表示标定后的三维坐标，单位为mm。
本文提出的标定方法全面考虑了透镜的径向畸变和切向畸变，当切向畸变较大时，该标定方法的精度明显高于鲁新国等[5]提出的线性摄像机标定技术。文章的标定方法完全采用线性方法求解摄像机参数，实验证明，
该方法计算简单，在单目摄像机基础上，双目立体摄像机标定方法快速、精确。
参考文献
[1] CHANG C C, JI Y F. Flexible videogammeric technique for three-dimensional structural vibration measurement. Journal of Engineering Mechanics, 2007,133(6):656-664.
[2] HU Jiuxiang, RAZDAN A, ZEHNDER J A. Geometric calibration of digital cameras for 3D cumulus cloud measurements[J]. Journal of Atmospheric and Oceanic Technology, 2009,26(2):200-214.
[3] SALVI J, ARMANGUE X, BATLLE J. A comparative review of camera calibration methods with accuracy evaluation [J].Pattern Recognition,2002,35(6):1617-1635.
[4] 邱茂林，马颂德，李毅.计算机视觉中摄像机标定综述[J].自动化学报，2000，26(1):43-55.
[5] 鲁新国，王琰，杨大为.基于计算机视觉的线性摄相机标定技术研究[J].沈阳理工大学学报.2007,26(5):43-46.
[6] 陈利红，毛剑飞，诸静.CCD摄像机标定与修正的简单方法[J].浙江大学学报（工学版），2003，37(4):406-409.
[7] 高立志，方勇，林志航.立体视觉测量中摄像机标定的新技术[J].电子学报.1999,27(2):12-14.
[8] TSAIRY.An efficient and accurate camera calibration technique for 3D machine vision [J].IEEE Transactions on Pattern Analysis and Machine Inteligence,1986.364-374.
[9] WENG Y, COHEN P,HERNIOU M. Camera calibration with distortion models and accuracy evaluation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(10):965-980.
[10] 张辉，张丽艳，陈江，等.基于平面模板自由拍摄的双目立体测量系统的现场标定[J].航空学报,2007,28(3):695-701.
[11] 丁丽娟，程杞元.数值计算方法[M].北京:北京理工大学出版社,2005.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容