图像融合的主要目的是综合各类图像数据的优点,提高图像的解译能力[1]。图像融合技术已广泛应用于军事、遥感、计算机视觉和医学等领域。目前比较典型的图像融合方法有:基于小波图像的融合方法两种[2-3]和基于数学形态学[4]的融合方法。这两种方法简单，容易实时处理，但是融合的精度不高,忽略了子图像中边缘信息细节丢失问题,从而影响了融合图像的清晰度和信息熵。
    多小波变换图像融合方法是在小波理论基础上发展起来的，多小波是指由两个或者两个以上的函数作为尺度函数生成的小波。夏明革[5]等人提出了在多小波变换域对低频系数和高频系数分别采用取绝对值最大和绝对值最小的融合规则。刘峰[6]等人提出了在多小波变换域对低频系数和高频系数分别采用基于区域均方误差加权平均的方法和区域能量匹配的方法。融合结果得到了改善，可是没有能够较好地保留原图像的细节和边缘。
    针对这一问题，本文给出了一种形态学多小波变换多聚焦图像融合方法。该方法利用不同的小波对待融合图像进行小波分解，利用一种新的抗噪型的形态学灰度形态梯度边缘检测算子来检测低频子图像边缘信息，以确保边缘信息的完整；对高频系数选择采用基于加权平均方法。本方法有效地防止了边缘信息丢失,提高了图像融合的质量。
1 数学形态学
    数学形态学[7-8]是一门建立在严格数学理论基础上的学科，其基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的。数学形态学的应用可以简化图像数据，保持它们基本的形状特征，并除去不相干的结构。数学形态学的基本运算有膨胀、腐蚀、开启和闭合(具体运算不作阐述)。
    灰度膨胀边缘检测算子：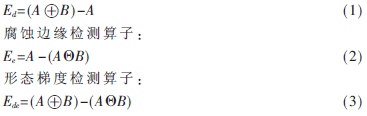

    由于灰度膨胀边缘检测算子主要是基于形态膨胀，得到的边缘信号较弱,所产生图像的边缘比较模糊。腐蚀边缘检测算子主要是基于形态腐蚀，它所得到的图像边缘信号较强，但是会增加图像的噪声。所以本文对传统的检测算子做了改进，采用结合形态学开启与闭合运算，提出了一种新的抗噪型灰度形态梯度边缘检测算子，其算子公式如下：

2 单一小波变换
    Mallat 提出了小波变换的快速分解算法与重构算法, 即利用两个一维滤波器实现对二维图像的快速分解, 再利用两个二维滤波器实现图像的重构。其对应的滤波器系数矩阵分别为H和G，则Mallat算法在j尺度下的分解公式[9]为：
 
3 多小波变换
    多小波变换是在单一小波理论基础上发展而来的，是建立在多分辨率分析基础上的,与单小波变换类似，如果生成多小波Ψ(x)相对应的多尺度函数Φ=(Φ1,Φ2,…,Φr)T满足r阶的多分辨分析MRA{Vj}，则称Φ是MRA^T的多尺度函数。如果Φ是正交的,则称{Vj}是正交的MRA^T。
    由多分辨率分析的定义可知，存在r×r矩阵Hk、Gk(r=2)，使得满足下列两个尺度方程[10]:

4 基于形态学多小波变换图像融合算法
    假设两幅待融合图像F和E，经过小波N层分解，分解得到不同的频率域，在不同的频率域选用不同的融合规则得到合成图像的多分辨率分解, 然后重构得到融合图像。多小波变换图像融合流程图如图1所示。

    下面分别对低频域和高频域给出各自的融合算法。高频系数反映了图像的细节，其选择规则决定了融合图像对原图像细节的保留程度。本文在选择高频系数时，采用基于加权平均的方法，对两幅图像多小波分解后高频系数取平均值：

式中，Dj为融合后图像在第j级的高频系数,DjF为图像F在第j级高频系数，DjE为图像E在第j级高频系数。
    对于低频系数，采用一种新的抗噪型灰度形态梯度边缘检测算子对低频子图像进行边缘检测。由于形态梯度边缘检测需要确定梯度的方向以及模值，同时由于小波模值和形态梯度值的关系[12]，所以设定一个门限的模极大值ε，只需要沿着各个小波变换的方向来寻找大于门限的模极大值?着即可。
    对于图像F定义如下：

式中，VF、VE包含了水平方向、垂直方向以及对角线方向上的边缘信息，因此本方法的角度μ取垂直、水平和对角线4个方向，沿着这4个方向搜寻多小波变换模极大值，就能够找到在该方向上的边缘信息。对于VF和VE，选择其中值较大的一个所对应的系数作为融合图像的低频系数，就能最大程度地在融合图像中保留原图像的边缘细节。
5 仿真实验与结果分析
    为了说明本文算法的有效性，在MATLAB7.0实验环境下,采用聚焦点不同的两幅图像做了实验。根据本文所提出的方法，对Floclo图像和Veg图像进行了仿真实验，并且与传统的图像融合方法进行了比较。其结果如图2、图3所示。

     从主观效果来看，本算法能够较好地保留细节部分，相对比其他几种传统的图像融合方法，本方法有明显的优势。为了更好地给出Floclo和Veg图像融合算法的性能评价，引入熵值[13]来进行评价，如表1所示。

    图像的熵值的大小反映了图像所包含的平均信息量的多少，图像的熵定义：

式中，H为图像的熵，N为图像灰度级，pi为像素级为i的出现的相对频率。
    本文主要针对图像融合中边缘信息容易丢失等问题，提出了一种形态学多小波变换多聚焦图像融合方法。该方法采用一种新的抗噪型形态学灰度形态梯度检测算子检测小波分解后低频子图像边缘信息，采用加权平均法选择高频系数。将这一算法应用于两组多聚焦图像中，并与几种传统的图像融合方法进行了比较，对实验结果的分析得出，基于形态学多小波变换多聚焦图像融合方法的融合效果明显。
参考文献
[1] PIELLA G. A general framework formultiresolution image  fusion：from Pixels to regions[J].Information Fusion,2003,68(4):259-280.
[2] BURT P J，KOLCZYNSKI R J. Enhanced image capture through fusion[C]． Proceedings International Conference on  Computer Vision．1993.
[3] DE I,CHANDA B, CHATTOPADHYAY B. Enhancing effective depth-of-field by image fusion using mathematical  morphology[J]. Image and Vision Computing, 2006,24(12):1278-1287.
[4] Tao G Q， Li D P， Lu G H． On image fusion based on different fusion rules of wavelet transform[J]．Acta Photonica  Sinica，2004，33(2)：222.
[5] 夏明革，何友，苏峰. 基于多小波分析的图像融合算法[J]. 电光与控制，2005,12（2）：19-22.
[6] 刘峰，姬光荣，周立俭. 基于多小波分析图像融合算法[J]. 中国海洋大学学报，2007,37（1）：163-167.
[7] 唐常青.数学形态学方法及其应用[M].北京:科学技术出版社,1990.
[8] 戴青云,余英林.数学形态学在图像处理中的应用进展[J].控制理论与应用,2001,18(4):478-482.
[9] 杨福生.小波变换的工程与应用[M].北京:科学出版社,2000.
[10] 那彦，史林，杨万海.基于成像机理的多小波多聚焦图像融合[J]. 系统工程与电子技术，2004,26(11):1549-1551.
[11] 朱四荣，王迎春. 基于多小波变换的多聚焦图像融合[J]. 计算机工程与应用，2010,46(6)：169-171.
[12] 晁锐，张科，李言俊. 一种基于小波变换的图像融合算法[J]. 电子学报，2004，32(5):750-753.
[13] 燕文浩，马彩文，张鸣，等. 基于小波变换的图像融合新算法[J].光子学报，2006，35(4):638-640.