摘 要: 为了提高铁路机车中移频键控信号的测量精度,给出了一种利用FPGA和ARM处理器测量频率的方法。该方法在FPGA中利用量化时钟实时测量一组FSK信号周期长度,并将测量数据存储在FPGA内部设计的双口RAM中。FPGA通过设计的串口模块将测量数据送给ARM处理器,ARM处理器对产生测量误差的主要原因进行分析,并对上、下边频切换时产生的畸变数据进行处理,给出了时间间隔测量误差的分析和补偿方法。实验表明,该系统具有较好的抗扰动能力,能够满足一般工业现场测试速率和精度的要求。
关键词: 移频键控信号;载波频率;调制频率;畸变
在铁路运输系统中,利用轨道电路移频键控信号(FSK)判断运输状态,传输控制信号,不同的调制信号下的载波信号代表不同的控制指令,所以实时、精确地检测轨道电路移频信号对保证铁路安全、快捷运输十分重要。采用频谱分析法确定FSK信号参数时,FFT变换需要对信号进行整周期采样,而FSK信号既具有数字通信的优点,又具有非线性调制的特点,因此对所有信号进行整周期采样具有一定的难度[1]。采用高频量化脉冲测量信号周期方法可以避免这一问题,只要量化时钟和处理速度满足要求,就可以获得满意效果。
本文在FPGA中利用高频时钟对FSK信号进行采样,用ARM处理器对获取的数据进行分析,并对畸变数据进行补偿,从而得到轨道电路FSK信号高频载波及低频调制信号测量参数。
1 系统设计
FSK信号是一种利用低频信号调制载波信号后产生的正弦交流信号[2],该信号主要由高频载波f0和频偏信号Δf形成的上边频fh、下边频fL组成,两种载波频率在每个调制信号fm周期内呈交替变化。
若FSK信号可用周期信号S(t)表示,则FSK信号的数学表达式[3-4]为:
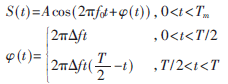
其中,f0为FSK信号的中心频率,?驻f为信号频偏,T=1/fm为低频调制信号周期。FSK信号如图1所示,其中虚线为低频调制信号,实线为载频信号段,中部为上边频段,两端为下边频段。

FSK信号测量的主要参数包括载频和频偏形成的上边频、下边频信号和调制频率三种物理量。在对FSK信号进行参数测量时,首先将FSK信号经过信号调理电路,利用高速开关管电路将正弦交流信号变换成方波信号;然后利用FPGA测量方波信号周期,并将测量数据通过串行接口发送给ARM处理器;ARM处理器接收到测量数据后,根据测量数据及数据统计情况计算载波和调制信号频率。在FSK信号幅值测量时,经过线性变换和限幅等处理,由高速16 bit A/D转换器进行转换。ARM处理器获取FSK信号频率和幅值参量后,将计算结果送往LCD显示。具体系统设计原理如图2所示。
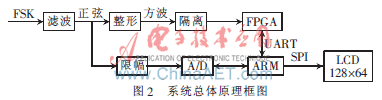
2 系统实现
移频键控信号测量时,通过测量一段时间内载波信号的脉冲宽度确定上边频和下边频,并根据载波信号切换点数据统计值确定调制信号频率。因此,根据载频信号的测量数据即可确定FSK信号参数。测量的移频信号主要为国产18信息和法国UM71移频信号两种制式,FSK信号的载频信号测量范围为495~2 611 Hz之间。
系统包括FPGA和ARM处理器两个核心模块,FPGA完成FSK参数测量,ARM处理器完成参数计算,如图3所示。根据FSK信号测量性能要求,选择Altera公司的Cyclone II系列FPGA作为测量核心模块。系统输入为25 MHz的时钟信号,经过FPGA中锁相环后获得30 MHz的时钟,利用该时钟对FSK信号的脉冲宽度进行量化,并将测量结果存储在16 bit字长的双口RAM中,利用FPGA中设计一个串口控制器,将FSK信号的测量值发送ARM处理模块。
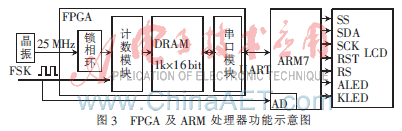
2.1 FPGA测量模块程序设计
FSK信号测量的准确性与量化时钟的选择有一定关系,而量化时钟的大小决定测量值的数据宽度[5-7],量化时钟选择越大,且存储测量结果的组数越多,则计算结果越精确,但在数据通信和数据处理时会影响系统的实时性。根据测量的FSK信号特征,在下边频为fL=495 Hz时,计数结果获得最大值。设量化时钟的频率为f,则必须满足f/fL=216,即量化时钟f<32 440 320 Hz。利用锁相环PLL产生30 MHz量化时钟信号,为了保证FSK信号测量精确度及测量结果不能溢出(超出预定的数据宽度),选择计数值的存储单位的数值宽度为16 bit。为获取有效的测量低频调制频率,应至少测量3个低频调制频率周期内部的方波计数值。由轨道移频信号的特征可知,当上边频fh=2 611 Hz、低频调制信号fm=10.3 Hz时,一个半周期内的调制频率内部最大的载波信号周期数n≤254,而3×254<1 024<5×254。因此选择测量FSK信号的数据深度为1 024组。
2.2 ARM数据处理模块程序设计
ARM处理器主要用来接收FPGA送来的FSK信号计数值,对计数值进行统计后得到载波信号频率、频偏和调制频率,并通过SPI接口将数据在LCD上进行显示。
数据处理的难度在于提高低频调制信号的测量精度,而影响系统测量精度的主要原因在于:FSK信号的上下边频切换为非整周期切换,导致切换点处出现畸变现象[4]。因而对畸变数据的判别及补偿的好坏程度是影响系统测量性能的主要因素。
在畸变数据判别时,首先在计数值的左侧和右侧分别取两个计数值CL1、CL2和CR1、CR2,如果|CL1-CL2|≤Δ1,|CR1-CR2|≤Δ1,且|CL1+CL2-CR1-CR2|≥2·Δ2时,则认为在计数值C处发生跳变,计数值C为畸变数据。其中,Δ1为计数允许的误差限,Δ2为载波频率切换判断限。通过对三组相邻畸变数据之间的计数结果取平均值,可以得到上边频和下边频的频率值,然后利用FSK信号相位连续方法对畸变数据进行补偿,依据下边频和上边频期间总的计数值累积获取低频调制频率。数据计算流程如图4所示。
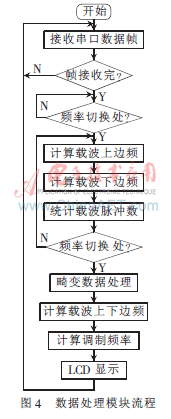
3 实验结果及分析
在系统实验测量过程中,分别对国产轨道电路18信息和法国UM71信号进行逐个测试。经实验发现,只要保证FSK信号的低频调制信号在取极值情况下获得满意精度,则在整个FSK测量范围内能够获得满意的性能。图5为通过对异常值进行剔除、对畸变值进行补偿后获取的误差曲线。通过误差分析可知,系统对FSK信号的高频载波信号测量误差为1×10-4,低频调制信号的测量精度为1×10-2,能够满足系统测量误差要求。系统测量更新速率为2 s左右,能够满足系统变化速率要求。
通过实验发现,该系统能够在2 s内准确地获取FSK信号的高频载波信号频率和低频调制信号频率。整个系统具有体积小、测量精度高等优点,满足我国电气化铁路和准高速铁路的测量要求,为设计快速、准确的FSK信号检测系统提供了依据,具有良好的发展前景。
参考文献
[1] SZPLET R, JACHNA Z, ROZYC K, et al. High precision time and frequency counter for mobile applications[J]. Wseas Transactions on Circuits and Systems, 2010, 6(9): 399-408.
[2] 王鹏,徐峰,王宏宇.利用FPGA实现移频键控信号的调制[J].清华大学学报(自然科学版).2002,42(S1):68-71.
[3] 魏学业,张勇,王琼洲.FSK信号实时检测系统研究(英文)[J].北方交通大学学报,1999(2).
[4] Jin Yu, Zheng Xifeng, Ding Tiefu. A high-accuracy parameter estimation algorithm for jointless frequency-shift track circuit[C]. Guangzhou City: IEEE Computer Society, 2008.
[5] 邵杨帆,李宏.准全同步频率测量方法的研究与实现[J].电子测量与仪器学报,2008,22(3):105-108.
[6] 张庚辰,秦京华.等精度可变多周期不间断测频方法的研究[J].仪器仪表学报,2000,21(6):651-653.
[7] 李鸣华,余水宝.基于过零点的信号分析与检测[J].仪器仪表学报,2004(z1):64-65.

