摘 要：提出了一种新的基于离散小波变换" title="小波变换" target="_blank">小波变换(DWT)与奇异值分解(SVD)相结合的数字图像水印算法。该算法将原始图像作小波分解并将小波分解得到的低频子带进行分块，对每一块进行奇异值分解后，选取每块中最大的奇异值通过量化的方法嵌入经过Arnold置乱后水印信息。水印的提取不需要原始图像，但受到密钥的限制，不知道密钥的人无法正确地恢复数字水印。实验结果表明，该算法具有较好的不可感知性、鲁棒性和安全性。
    关键词：离散小波变换；奇异值分解；盲水印；图像置乱；鲁棒性

    随着计算机网络的迅速发展和广泛应用，数字媒体的非法篡改、复制和盗版现象也越来越普遍，数字媒体的版权保护已成为迫切需要解决的问题。作为信息隐藏领域中的数字水印技术是实现多媒体版权保护与信息完整性保证的有效方法。它的基本思想是在数字图像、音频和视频等产品中嵌入秘密的水印信息以便保护数字产品的版权。对于数字水印技术，一般要求水印系统具有不可见性、鲁棒性和安全性。也就是说，水印必须是不可察、不可测和难于破坏的。
    目前，从实现角度看水印算法主要分为空域和变换域算法两大类。空域算法是直接对空域数据进行操作，变换域算法是在变换域中进行水印的嵌入与提取，如离散傅里叶变换(DFT)、离散余弦变换(DCT)和离散小波变换(DWT)^[1]等。与空域相比，变换域算法具有更好的鲁棒性。由于离散小波变换具有良好的多分辨率表示、时频局部分析特性，基于DWT变换域的数字图像水印算法的研究更是得到了普遍的关注。
    按水印的提取方法划分，水印算法又可分为提取时需要原图像和不需要原图像两种。前者称为非盲水印，后者称为盲水印。非盲水印算法在提取过程中需要原始图像，在版权认证的应用中，意味着需要大量的存储资源和计算资源，如果需要认证的数字作品数量很多，给定一个数字作品要去查找相应的原作品本身就很困难。近几年来学术界研究的数字水印算法大多数属于盲水印算法。
    本文提出的水印算法是一种新的基于小波变换(DWT)和奇异值分解(SVD)相结合的盲水印算法。这样可以充分利用DWT的多分辨率特性和SVD所固有的特征，增强了水印的不可见性和鲁棒性。在水印提取过程中不需要原始图像，但受到密钥的限制，提高了安全性。以下将详细介绍本算法的原理以及水印嵌入、提取的过程和实验结果。
1 基于DWT-SVD的水印算法
1.1 图像置乱
    所谓“图像置乱”，可以表示为R:U→U、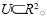其中，R表示映射，R²表示二维空间，即图像置乱是二维空间的一个映射。任何具有可逆特性的映射都可用于图像置乱。置乱的作用是改变原图像的排列组合方式及空间相关性。用得较多的置乱技术是基于Arnold变换、幻方变换、分形Hilbert曲线、IFS模型、Conway游戏和Gray码变换等方法。
    Arnold变换是Arnold在研究环面上的自同态时提出的，后来被应用到数字图像上。从采样原理分析，数字图像可看作是在二维连续的曲面上，按照某一间隔和某种策略进行采样所得到的一个二维离散点的阵列，即一个图像矩阵。对于一幅大小为N×N的图像A，用公式(1)进行Arnold变换：
    
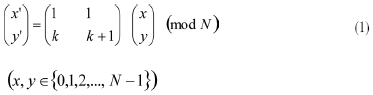
式中，(x, y)是原图像的像素点，(x’, y’)是变换后新图像的像素点，N是图像阶数即图像的大小，一般考虑正方形图像，k是属于[1, N]的一个整数。记变换矩阵为A，由此，做迭代程序：
   
式中，n代表迭代次数，整个迭代过程呈周期性，即当此图像经过一定周期的迭代后会重现原图像。由此，可见，Arnold变换算法简单直观且具有周期性，因此，本文选取Arnold变换对水印图像进行预处理，其置乱次数及k可作为隐藏系统的密钥，从而提高了系统的安全性和保密性。
1.2 图像的小波变换
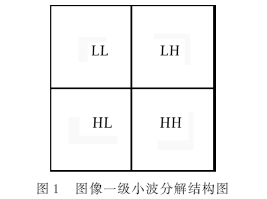
    小波变换是近几年兴起的一个崭新的信息分析理论，是一种新的可达到时域或频域局部化的时-频域分析方法，具有多分辨率分析的特点。利用小波变换可以提高水印在视觉上的隐蔽性和稳健性。图1是一个小波一级分解示意图，通过一级小波变换，原始图像被分解为4个一级子图，即1个低频子带图像LL和3个高频子图：水平细节子带图像HL、垂直细节子带图像LH、对角细节子带图像HH。其中LL集中了图像的大部分能量，可以继续分解。

1.3 SVD特性分析
    数值分析中的奇异值分解(SVD)是一种将矩阵对角化的数值算法^[2]。从线性代数的角度，一幅灰度图像可以被看成是一个非负矩阵。若一幅图像用A表示定义为A∈R^M×N，其中，R表示实数域，不失一般性，假设M[3]:
   
式中，都是正交矩阵，Σ是一个对角矩阵，其对角线上的元素满足:
   
    σ_i是由该分解所唯一决定的，叫做A的奇异值，它也是AA^T的特征值的平方根。分解式UΣV^T称作A的奇异值分解。奇异值分解具有如下3个显著特性：(1)奇异值所表现的是图像的内蕴特性；(2)图像奇异值的稳定性非常好，在图像被施加小的扰动时，其奇异值不会有大的变化；(3)在对图像做奇异值分解所得的奇异值序列σ_i中，第一个奇异值比其他奇异值大得多^[4]。
    从数字水印的角度，在奇异值中嵌入水印，利用图像奇异值的第1个特性使得水印嵌入算法具有很好的不可见性；第2个特性确保水印具有很好的鲁棒性；第3个特性为选择奇异值的方法提供了依据，因为块奇异值分解会产生更多具有较大数值的奇异值，这对水印嵌入是有利的，所以本文采用块奇异值分解。
1.4 水印的嵌入
    设I为载体图像，W为水印图像。
    (1) 利用公式(1)和(2)对水印图像W进行Arnold置乱变换后得到W’，其中k和置乱次数可以作为密钥。
    (2) 对载体图像I (大小为M×N)进行一级小波分解，得到3个高频子带HH、LH、HL和1个低频子带LL；将低频子带图像按m×n分块，则低频子带图像所能嵌入水印的最大bits数为：round(M/2m)×round(N/2n)，即如果水印的像素点数超过了该值，则无法嵌入该水印，或者必须先对水印进行尺度变换，减少信息量。

    (3) 对每一块进行奇异值分解(SVD)，Block_i=U_iΣ_iV_i^T并让Σ_i中的奇异值σ_i按降序排列。
    (4) 对每块中的第1个值σ_i按以下规则进行修改(令Z=σ_is1mod q):
    ① ifW_(i,j)^'=1 ，则：
   
    式中，q为嵌入强度因子，W_(i,j)^'为相应块所嵌入置乱后的水印信息，嵌入水印后的块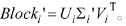
    (5) 重复(3)、(4)直至嵌入所有的水印信息，再进行小波的逆变换即可得到水印后的图像。
1.5 水印的提取
    水印提取是水印嵌入的逆过程，该算法最大的优点是提取水印不需要原始图像。其提取过程如下：
    (1) 将待检测图像进行一级小波分解，将得到的低频子带图像按m×n分块。
    (2) 对每一块进行奇异值分解(SVD)，Block_i^'=U_iΣ_i^'V_i^T，并让σ_i^'中的奇异值Σ_i^'按降序排列。
    (3) 按以下规则对σ₁^'进行修改(令Z=σ₁^'modq)：
   
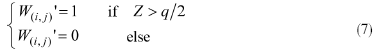
    (4) 重复(2)、(3)直到所有低频子带的块嵌入的水印信息都得到提取。
    (5) 将提取出的W`通过保存的密钥进行Arnold的反变换，即可获得原始水印信息W。
2 实验结果
    为了检验本算法水印的鲁棒性和不可见性，本文采用2个常用指标值来进行度量。
    (1) 归一化相似度NC，度量所提取的水印与原始水印的相似程度，NC定义为：
   
    (2) 峰值信噪比PSNR，度量隐秘载体图像与原始图像之间的质量差别，PSNR定义为：
   
    实验平台为Matlab6.5仿真平台，原始载体图像为标准灰度图像Boat(512×512×8)、水印为32×32像素的二值图像如图2所示。本文采用haar小波基，将载体图像Boat一层小波分解后，将低频子带图像系数分成1024个8×8大小的块。为了实验的视觉效果，LL频带选取的嵌入强度因子q=130，密钥的值取k=158，迭代次数n=13。

    (5) 图像裁减
    对图2(c)进行不同部位的任意裁减，载体图像和提取出的水印如图5所示。

     
    (6) 模糊和锐化攻击
    对图2(c)分别进行模糊和锐化处理，载体图像和提取出的水印如图6所示。

    (7) 算法比较
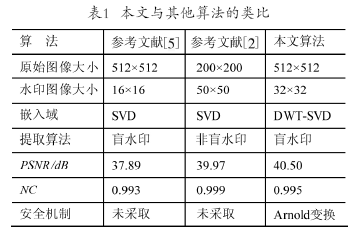
    图像水印的攻击测试方法有很多，上述攻击测试的结果已经可以证明本文提出的算法具有很好的鲁棒性。为了突出这种算法的性能，本文将其与几种相关的典型算法进行了类比，其结果如表1所示。虽然参考文献[2]也是使用了SVD分解的盲水印算法，但通过攻击测试，不难发现本文提出的算法鲁棒性更好。选用标准512×512×8灰度图像Lena和Peppers进行对比实验，其结果如表2所示。

    本文提出了一种在小波变换域的低频子图中基于块奇异值分解的量化水印算法，这种基于DWT-SVD的水印技术充分结合了小波变换的多分辨率、时频局部的特点和奇异值的3个特性，具有如下特点：
    (1) 水印是一幅人眼可识别的有意义的二值图像，增加了水印的可证明性。
    (2) 通过Arnold置乱后的水印嵌入增加了水印的安全性。
    (3) 基于块奇异值分解的量化水印算法充分利用了奇异值的3个特性，保证了水印的不可见性；水印嵌入的位置选择小波变换的低频域，并选择块奇异值中的最大值进行嵌入增强了算法的鲁棒性。
    (4) 该算法是盲水印算法，提取水印不需原始图像，算法复杂度低。
    实验结果表明，此方法鲁棒性和不可见性好,简单易实现，能抗各种图像处理攻击，是一种行之有效的图像鉴定方法。
参考文献
[1] JIN Cong, TAO Feng,FU Yu. Image walermarking based HVS characteristic of warelet transform.International Conference on Intelligent Information Hiding and Multimedia signal Processing,Pasadem,Califdrnia,USA IEE Computor Society 18.20 December 2006: 71-74.
[2] 周波，陈健. 基于奇异值分解的、抗几何失真的数字水印算法[J]. 中国图像图形学报, 2004, 9(4):507-512.
[3] Gass S I, Rapcsak T. Singular value decomposition in AHP [J]. European Journal of Operational Research, 2004,154(3):573- 584.
[4] 刘瑞桢,谭铁牛.基于奇异值分解的数字图像水印方法[J].电子学报,2001,29(2):168-171.
[5] 胡志刚,谢萍,张宪民.一种基于奇异值分解的数字水印算法[J].计算机工程,2003,29(17):162-164.