摘  要： 针对现有融合方法存在的光谱信息和空间细节信息不能较好兼顾的问题，提出了一种遥感图像小波融合算法。根据高分辨率遥感图像自身的空间尺度，采用多进小波分析技术较好地解决了不同尺度遥感图像空间细节的表达问题，同时利用基于方向能量统计量的自适应融合准则较好地解决了融合中的光谱信息保留问题。实验结果表明，该融合方法在保持全色图像的高空间分辨率的同时，提高了融合图像的光谱保持度。
关键词： 高空间分辨率；图像融合；多进小波变换；方向能量统计量；光谱保持度

　随着传感器技术的不断进步，遥感卫星的空间分辨率不断提高，数据源和图像数据量的增多是当前遥感技术发展的趋势[1]。数据融合技术是提高数据利用率的有效方法之一，目前经典的遥感图像融合算法主要有IHS变换融合算法、PCA变换融合算法和小波变换融合算法等。IHS融合算法从人类的色彩感觉角度将表征空间分布的物理量I与表征光谱特征的物理量H和S分离出来，用全色图像替换I分量后，经IHS反变换得到融合图像。但IHS融合算法将产生光谱失真现象。PCA变换作为一种统计学上的多维正交线性变换，通过研究R、G、B 3组数据的相互数学关系，经统计变换，给出最大特征值对应的特征向量，然后用全色波段来替换该特征向量。
　小波变换兴起于20世纪80年代中期，引起了信号处理和图像处理领域的广泛兴趣。MALLAT首先将小波技术引入到图像处理领域，DAVID首先利用小波技术实现了多光谱和全色的遥感图像融合[2]，利用小波进行图像融合迅速成为研究热点。基于小波分析的图像融合算法主要是利用人眼对局部对比度的变化比较敏感这一现象，根据一定的融合规则，在多幅原图像中选择出最显著的特征，并将这些特征保留在最终的融合图像中，其缺点是融合图像存在一定程度的振铃效应和空间细节丢失现象。
本文提出了一种自适应的多进小波变换图像融合算法，根据全色图像和多光谱图像的空间分辨率关系分别设计了相应的多进小波分解方法，这种方法保留了图像本身固有的尺度；根据融合数据源的不同特点，设计了两个不同的小波系数特征统计量，减少了传统二进小波带来的空间细节信息丢失和振铃模糊效应。
1 多进小波变换
小波分析在图像处理中具有非常重要的地位，它克服了傅里叶变换单一分辨率的缺陷，具有多分辨率分析的特点，同时在时域和频域都有表征信号局部信息的能力。因此，基于小波分析的图像融合算法是近年来研究的热点。但是目前基于小波分析的图像融合研究主要集中在融合规则方面[3]，这也是近年来像素级图像融合研究的主流。
　多进小波分析是近年来发展起来的小波理论的一个重要分支。它在对称性、光滑性和紧致性等方面都优于二进制小波；它将频带分解更细，为在不同的频带而采用不同的融合提供了有利条件，为融合算法提高了灵活性。多进小波的基本构造理论是多分辨分析。设M≥2，则平方可积空间L2（R）上的一个多分辨分析是满足以下条件的闭子空间列：


2.3 算法具体步骤

　本文的融合思路是：首先对多光谱图像进行IHS变换，将表征地表辐射能量和空间分布的物理量I分量与表征光谱信息的H和S分量分离开来；接下来进行I分量与全色图像的融合；然后进行IHS反变换；最后得到融合图像。
　基于上述分析，本文提出的基于内容自适应多进小波融合算法步骤如下：
　（1）将多光谱图像插值到全色图像尺寸大小，重采样方式采用双线性内插法，然后对其进行IHS变换。
　（2）对全色图像和多光谱图像进行IHS变换后的I分量进行小波分解。
　（3）分别对I分量和全色图像的高、中、低频小波系数进行特征量统计并进行比较。
　（4）一致性检验。通过步骤（3）确定融合图像的小波系数后，对不同频带的融合权值作进一步的调整和加权，以保证不同小波频带具有连续的灰度变化和一致性的空间细节。
　（5）将融合后的图像作为I分量，与多光谱IHS分量的H和S分量进行IHS反变换，从而得到融合图像。
该算法的步骤如图3所示。

3 实验结果及性能分析
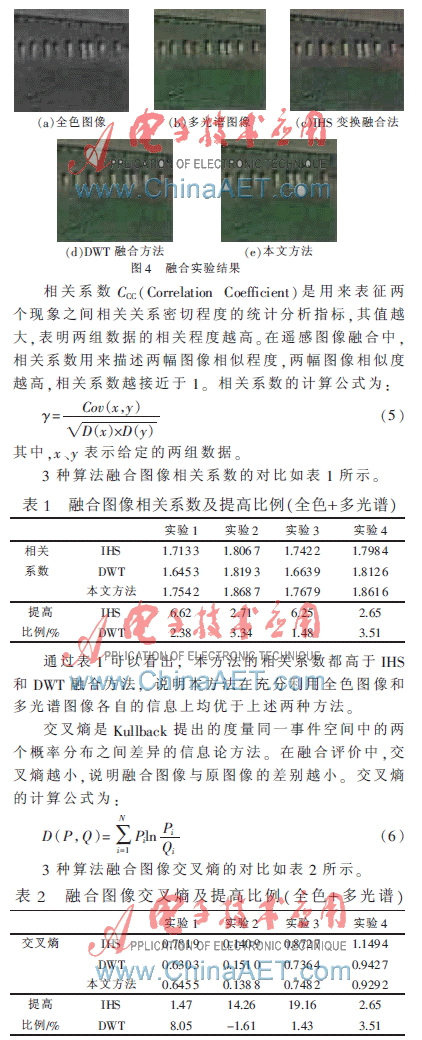
　本文的实验数据为Ikonos和Quickbird高分辨率遥感图像。全色波段和多光谱波段的分辨率之比为1：4。因此，选用支撑长度为8的4进对称正交小波，小波基选用Daubechies8，对称性保证了相位不失真。在全色波段中，图像纹理是一种常用的空间信息，纹理特征依赖于提取纹理时所采用尺度的大小。图像尺寸为1 170×920。图4（a）为全色影像，图4（b）为多光谱影像，图4（c）为IHS变换融合，图4（d）为传统二进小波融合方法，图4（e）为本文所采用的方法。从实验融合效果的主观质量来看，IHS融合方法图像的清晰度最高，但是光谱失真最大；DWT融合方法光谱保持度最好，却存在一定的振铃模糊；本文提出的方法图像的清晰度较高，光谱保持度较高。

　　通过表2可以看出，虽然本文采用的方法在光谱的利用上没有DWT算法好，但从总体评价来看，该融合方法改善了融合图像的空间细节信息和光谱信息，从而提高了图像的目标识别率和光谱保持度。
基于方向能量统计量的自适应多进小波融合算法充分利用了高空间分辨率遥感图像的空间细节特征、图像边缘和方向性特征信息，同时保留了多光谱图像的光谱信息特征，有效地解决了IHS变换中融合图像光谱信息丢失较多以及传统二进小波产生振铃模糊效应等问题。
参考文献
[1] RANCHIN T， WALD L. Fusion of high spatial and spectral resolution images： the ARSIS concept and its implementation[J]. Remote Sensing， 2000，66（1）：49-61.
[2] LI H， MANJUNATH B S， MITRA S K. Multisensor image fusion using the wavelet transform[J]. Graphical Models Image Process， 1995，57（3）：235-245.
[3] Wang Zhijun， ZIOU D， ARMENAKIS C， et al. A comparative analysis of image fusion methods[J]. IEEE Transactions on Geoscience and Remote Sensing， 2005，43（6）：1391-1402.
[4] WANGA L， SOUSAB W P， Gong Peng， et al. Comparison of Ikonos and Quickbird images for mapping mangrove species on the Caribbean coast of Panama[J]. Remote Sensing of Environment， 2004（9）：432-440.
[5] DAUBECHIES I.小波十讲[M].李建平，杨万年，译.北京：国防工业出版社，2004.
[6] 王智均，李德仁，李清泉.利用小波变换对影像进行融合的研究[J].武汉测绘科技大学学报，2000，25（2）：137-142.