摘 要: 介绍了快速傅里叶变换(FFT)算法的原理,利用DSP实现了FFT算法,利用TMS320F2812 DSP内部的ADC模块与事件管理器的定时器实现信号的实时采集。分析了DSP中数据采集ADC的功能。基于CCS调试软件显示了输入输出信号波形。在CCS环境下,采用C语言编程,实现了FFT算法和离散余弦变换。
关键词: DSP;快速傅里叶变换;A/D转换;离散余弦变换
傅里叶变换是一种将信号从时域变换到频域的变换方式,而快速傅里叶变换FFT(Fast Fourier Transform)是数字信号处理技术的基石。FFT和离散余弦变换DCT(Discrete Cosine Transform)都是数字信号处理技术中的基本算法,也是数字信号处理的基本工具。DSP芯片的出现使FFT和DCT的实现更为方便。本文利用TMS320F2812 DSP内部的ADC模块与事件管理器(EVA)构建了数据采集与数据变换并行处理的信号处理系统,充分利用TMS320F2812强大的数据处理能力,实现了FFT运算,提高了运算速度[1-2]。
1 FFT算法的实现
TI公司的TMS320F2812 DSP是目前控制领域性能较高的处理器,它将各种高级数字控制功能集成于一块芯片上,整合了Flash存储器、快速的A/D转换器等外设,强大的数据处理和控制能力大幅度提高了应用效率。
1.1 数据采集ADC功能
DSP系统的模拟输入电压范围为0~3 V。通过使用事件管理器的定时器1下溢中断启动ADC。系统设计时晶振为30 MHz,经过锁相环倍频后CPU时钟频率SYSCLKOUT是150 MHz,事件管理器采用高速外设时钟HSPCLK,经过程序设计6分频得到高速外设时钟HSPCLK为25 MHz。
SysCtrlRegs.HISPCP.all=0x3;//HSPCLK= SYSCLKOUT/6
将事件管理器中通用定时器1的周期寄存器值设置为0x07FF,每经过2 048(0x07FF+1)个通用定时器的时钟周期启动一次ADC。事件管理器中的通用定时器1由于没有对高速外设时钟分频,因此通用定时器1的时钟频率为25 MHz。
EvaRegs.T1PR=0x07FF;//设置通用定时器1周期寄存器
EvaRegs.GPTCONA.bit.T1TOADC=1;
//通用定时器1启动ADC
EvaRegs.T1CON.all=0x1042;
//通用定时器1连续增计数模式,不分频,采用HSPCLK
为了实现数据采集,设置ADC工作在级联排序器模式,最大转换通道数为1,并且采集数据来自通道ADCINA4,使能事件管理器EVA的触发信号启动ADC排序器SEQ1,允许ADC产生中断。相关程序设计如下。
AdcRegs.ADCTRL1.bit.SEQ_CASC=1;//级联排序器模式
AdcRegs.ADCMAXCONV.all=0x0000;
//设置1个转换通道AdcRegs.ADCCHSELSEQ1.bit.CONV00=0x4;
//设置转换通道ADCINA4
AdcRegs.ADCTRL2.bit.EVA_SOC_SEQ1=1;
//使能EVA的触发信号启动排序器SEQ1
AdcRegs.ADCTRL2.bit.INT_ENA_SEQ1=1;
//使能SEQ1产生的中断请求
当事件管理器的通用定时器1产生下溢中断时,启动ADC。在ADC转换完成中断服务程序中读取12 bit A/D转换结果。程序设计如下:
interrupt void adc_isr(void)
{
px[ConversionCount]=AdcRegs.ADCRESULT0>>4;
if(ConversionCount==128)
{ConversionCount=0;}
else ConversionCount++;
AdcRegs.ADCTRL2.bit.RST_SEQ1=1;
//复位排序器SEQ1
AdcRegs.ADCST.bit.INT_SEQ1_CLR=1;
//清除排序器SEQ1中断标志位
PieCtrlRegs.PIEACK.all=PIEACK_GROUP1;
//写1清零中断应答寄存器PIEACK相应位,
//以便能够响应该组随后的中断
return;
}
1.2 FFT算法原理与程序流程图
FFT是DFT的快速运算。由于有些信号在时域很难看出特性,使用FFT将其变换到频域,就会很容易看出其特性。DFT算法的基本公式为:

2 DCT的实现
2.1 DCT基本原理
DCT是一种与傅里叶变换紧密相关的数学运算。在傅里叶级数展开式中,如果被展开的函数是实偶函数,则其傅里叶级数中只包含余弦项,再将其离散化可导出余弦变换,因此称之为离散余弦变换。DCT被认为是性能接近K-L变换的准最佳变换,是对语音和图像信号进行变换的最佳方法。DCT变换的快速算法有以下两种方式:
(1)由于FFT算法的普遍采用,直接利用FFT实现DCT变换的快速算法相对容易。但是这种方法也有不足之处,即计算过程会涉及复数的运算。由于DCT变换前后的数据都是实数,计算过程中引入了复数,而一对复数的加法相当于两对实数的加法,一对复数的乘法相当于4对实数的乘法和两对实数的加法,显然是增加了运算量,也给硬件存储提出了更高的要求。
(2)直接在实数域进行DCT快速变换。显然,这种方法的计算量和硬件要求都要优于前者。鉴于此,本文采用第二种方法实现DCT变换的快速算法。
给定序列x(n),n=0,1,…,N-1,其离散余弦变换定义为:


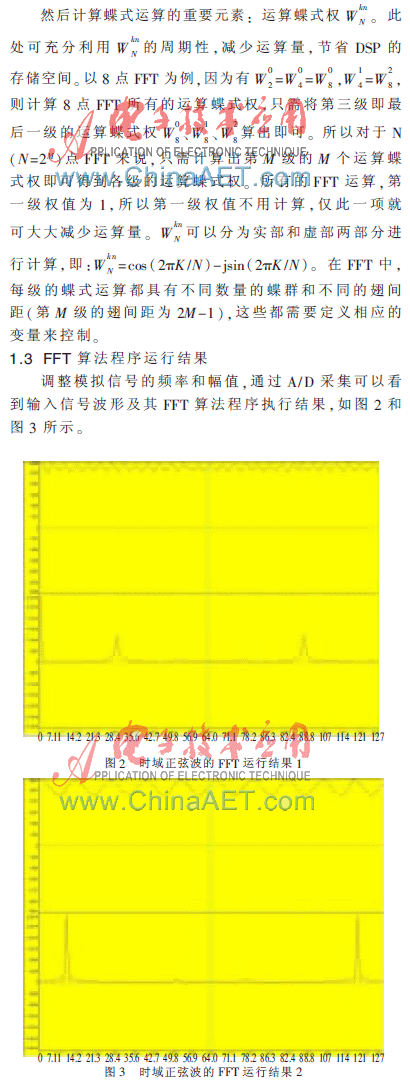
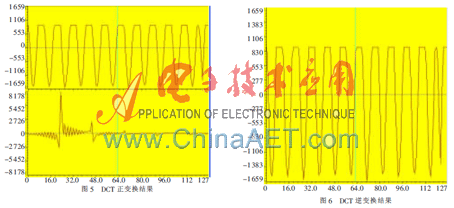
图5为正变换结果,其中上方为输入信号,下方为输出信号。图6为逆变换输出结果,此输出波形与图5的输入波形一致,由此可以验证程序的正确性。
本文说明了数据采集ADC的功能和FFT算法的原理以及程序设计流程图,在CCS调试平台下,采用C语言编程实现了FFT算法,并且实时性好。阐述了离散余弦变换DCT基本原理,基于TMS320F2812 DSP实现了离散余弦变换。程序运行结果表明,DSP能够快速高效地完成一系列数字信号处理算法[4]。
参考文献
[1] 贾玮,杨录,张艳花.基于TMS320VC5416的FFT算法的实现[J].山西电子技术,2009(2):11-13.
[2] 万浩平,马进,王锋.基于TMS320F2812的高精度数据采集及FFT实现[J].工业控制计算机,2009,22(4),54-55.
[3] 胡广书.数字信号处理[M].北京:清华大学出版社,2003.
[4] 伍小芹,吴秋丽.FIR数字滤波器在DSP上的实现[J]. 现代电子技术,2007(1):85-87.

