摘 要: 针对纹理图像分割问题的研究,经典的多尺度MRF方法是对不同尺度的纹理特征仅通过多尺度序列下的MRF邻域系统进行描述。为了更加准确地描述纹理特征,将从空间分布特性与MRF邻域系统两个方面综合考虑,提出一种带有联合灰度信息的灰度共生矩阵与多尺度MRF相结合的方法。实验结果表明,该方法能够有效地提高分割准确度。
关键词: 纹理图像分割;灰度共生矩阵;多尺度;MRF
纹理作为一种自然属性,在一定程度上反映了物体的特征,并且纹理具有抗遮挡能力强、受环境影响小等特点,因此常被用于区分背景与其他物体。通常情况下,纹理可以采用基于模型的MRF(Markov Random Field)方法进行描述。单尺度MRF模型是空域模型,常采用贝叶斯法进行图像分割。多尺度MRF模型是在不同分辨率的图像上进行分析,它能捕捉到不同分辨率图像的结构信息以及具备更强的空间描述能力,并且还具有计算复杂度低、收敛速度快、减少过分割现象和较强的抗噪性能等特点[1],因此多尺度MRF图像分割受到广泛关注。近几年研究中,陈晓惠等人[2]将形态小波域多尺度马尔可夫模型应用于纹理图像分割中,该模型结合了形态小波和MRF各自的优势,能够对图像进行非线性多尺度分解,因此提高了对纹理特征的描述。对于多尺度MRF分割方法,不同尺度的纹理特征仅通过多尺度序列下的MRF邻域系统进行描述,并且在起始分割中仅考虑了灰度特征而忽略了邻域系统特性和像素在空间中的排列信息。在统计方法中,灰度共生矩阵能够有效地从空间中提取纹理特征[3],并且灰度共生矩阵与MRF之间存在关联性,其中3个不相关的二次统计量就可作为纹理特征描述。仅用灰度信息、距离判定、无邻域系统相关性或空间相关性描述纹理特征,具有一定的局限性。为了解决该问题,本文提出将带有灰度信息的灰度共生矩阵与多尺度MRF相结合的方法进行纹理图像分割。
1 多尺度MRF与灰度共生矩阵下的纹理结构
1.1 多尺度MRF
原始图像经过小波分解后可得到具有不同尺度的图像数据,并依据尺度大小关系组成金字塔结构。然后,在最大尺度图像上利用低频信号建立最大尺度下的MRF,再依次以上层分割结果作为下层分割的基础[4]。
图像的多尺度MRF模型是通过建立特征场与标号场来描述数据信息的。多分辨率特征场的多尺度序列表示为Y={Y0,Y1,…,YJ-1},标号场表示为X={X0,X1,…,XJ-1},其中特征场描述数据的特征,标号场描述分割结果的类别[2]。通常采用MRF二阶邻域系统(即某一像素与其邻近像素的关系)的形式来表示纹理特征,如图1所示。由于二阶邻域系统未能详细地描述出像素的空间排列信息,因此在分割过程中可能会漏掉某些特征信息。

与MRF不同,二次统计量是在空间分布上对纹理信息进行描述[5]。灰度共生矩阵在描述纹理时缺少了局部细节信息,可以通过MRF的邻域系统来弥补。反之,MRF空间信息的缺失也可以通过灰度共生矩阵得到补充。
2 基于灰度共生矩阵和多尺度MRF的纹理图像分割
以灰度共生矩阵为基础提取的3个互不相关的二次统计量熵、对比度与相关性,可以很好地从空间分布方面来描述图像的纹理[6]。为了更加准确地描述纹理特征,可将3个互不相关的统计量与灰度信息共同用于描述最大尺度下的纹理信息,形成特征矩阵C=[f1 f2 f3 f4],然后进行FCM聚类。

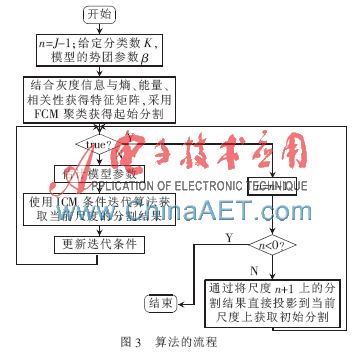
基于灰度共生矩阵和多尺度MRF图像分割方法流程如图3所示,具体步骤如下:
(1)设定图像的分类数K、势团参数β以及算法迭代次数。
(2)对图像作n=J-1层小波分解,利用灰度共生矩阵提取特征,并与灰度信息共同获得特征矩阵,利用FCM获得起始分割结果。
(3)由聚类算法的标号计算出尺度J上的标号场能量,进行参数估计,计算特征场能量,利用能量最小原则,得出该尺度分割结果。
(4)将该尺度的计算结果直接映射到最邻近的高分辨率图像上作为初始分割。
(5)进行参数估计,计算标号场能量,计算特征场能量,更新迭代条件当能量最小时计算停止。
3 实验结果与分析
选取256×256的合成纹理图像、256×256的遥感图像和来自Berkeley图像库编号为86016的481×321自然景物纹理图像。实验选取灰度共生矩阵步长为1,方向选取0°、45°、90°、135°。纹理合成图像灰度共生矩阵选取7×7的滑动窗口,势团参数=5.5,迭代100次;遥感图像选取5×5的滑动窗口,势团参数β=0.9,迭代50次;自然景物图像选择33窗口,势团参数β=0.9,迭代50次。实验平台为Matlab 7.8.0,图4为分割效果图,其中,第1列至第5列分别为:实验原图、手工标注图、灰度共生矩阵分割结果、多尺度MRF分割结果、本文方法分割结果。为了能够定量分析分割结果,本文将采用整体分类精度和Kappa系数作为评价指标,结果如表1所示。

从表1可以看出,针对3种类型纹理图像,本文方法获得的分割结果要明显优于灰度共生矩阵法与多尺度MRF法。其中,对于合成纹理图像,本文方法的整体分类精度为99.03%,Kappa系数为97.95%,均高于灰度共生矩阵法与多尺度MRF法;对于遥感图像,本文方法的整体分类精度为96.66%,Kappa系数为90.12%,均高于灰度共生矩阵法与多尺度MRF法;对于自然景物图像,本文方法的整体分类精度为98.34%,Kappa系数为96.13%,也均高于灰度共生矩阵法与多尺度MRF法。综合考虑,在平均整体分类精度方面,本文方法比多尺度MRF法高出2.96%,比灰度共生矩阵法高出5.94%;在平均Kappa系数方面,本文方法比多尺度MRF法高出1.72%,比灰度共生矩阵法高出12.12%。实验表明,本文提出的纹理图像分割方法不仅提高了分割准确度,还提高了分割的一致性。
本文提出了一种基于灰度共生矩阵和多尺度MRF纹理图像的分割方法。首先,采用小波分解获得图像各个尺度的数据信息,之后在最大尺度上结合灰度信息以及由灰度共生矩阵获得的二次统计量进行FCM聚类,作为最大尺度上MRF的起始分割;其次,依照起始分割的标号再进行当前尺度MRF的分割,建立特征场与标号场,获得当前尺度最终的分割结果;最后,当前分割结果作为邻近高分辨率图像的起始分割再进行优化。实验表明,本文方法分割纹理图像的准确度与Kappa系数高于多尺度MRF方法和灰度共生矩阵的方法。在后续的研究中,将探讨如何提高算法的运算速度。
参考文献
[1] 刘国英,马国锐,王雷光,等.基于Markov随机场的小波域图像建模及分割[M].北京:科学出版社,2010.
[2] 陈晓惠,郑晨,段汕,等.形态小波域多尺度马尔可夫模型在纹理图像分割中的应用[J].中国图象图形学报,2011,16(5):761-766.
[3] 韦玉春,汤国安,杨昕,等.遥感数字处理教程[M].北京:科学出版社,2009.
[4] Zheng C, Liu G, Hu Y, et al. Image segmentation based on multiresolution Markov random field with fuzzy constraintin wavelet domain[J]. IET Image Process,2012,6(3):213-221.
[5] MRIDULA J, KUNDAN C, DIPTI P. Combining GLCM features and Markov random field model for colour textured image segmentation[C]. IEEE Conference on Devices and Communications(ICDeCom2011),2011:1-5.

