0 引言

    在实际的工作环境中，遥感图像在其光学信息获取转换和传输过程中通常会受到噪声干扰而引起图像质量下降,从而变得模糊, 因此遥感图像的去模糊分析、评估和滤波作为遥感图像处理的研究热点一直受到遥感应用领域的关注^[1]。遥感图像去模糊的主要目的是在去掉模糊的同时保持遥感图像的边缘和重要的特征信息。目前对遥感图像的去模糊方法主要有变换域和图像域的处理方法。变换域的处理方法如Donoho等提出的著名的小波阈值方法^[3]；在小波域下变换的方法去除模糊^[2]；Elad等人通过字典学习利用前向滤波过程进行去模糊等^[10]。图像域的去模糊主要包括基于回归的bilateralfilter去模糊、PDE方法去模糊和Nonlocal的方法等^[6-7]。近年来，基于超完备稀疏分解的信号表示理论得到广泛关注，并取得巨大成果。其基本原理是利用超完备字典中的冗余基取代正交基，对字典的选择尽可能地包含分解信号的信息。对信号的稀疏分解就是从超完备字典当中选择出最佳线性组合的若干原子来表示信号，能极大地降低高分辨率遥感图像的存储、传输、处理的所需资源，将该方法应用于高分辨率遥感图像的去模糊中，能够取得较好的结论^[8]。

    本文针对“高分一号”遥感图像高分辨率与大视场相结合、多载荷图像拼接融合应用的特点，提出一种基于稀疏表示和快速梯度投影算法。该算法通过对模糊图像的特迭代处理,从而达到滤除遥感图像模糊的目的。本文建立了基于稀疏表示和快速迭代投影的模型，并以理论和实验证明了本算法的有效性。

1 基于压缩感知的遥感图像去模糊模型

1.1 基于稀疏表示的遥感图像处理模型

    任一理想的遥感图像可以表示为y₀∈R^N，A为线性模糊算子，可以对图像进行均匀线性模糊或者高斯低通滤波，则遥感图像的模糊操作可以建模为^[9-11]：

1.2 对模型的求解

    根据Beck等人提出的快速梯度投影(Gradient Projection Algorithm，GPA)算法^[15]，对式（1）中的第一部分f(x)，由于其是光滑且凸的，具有Lipschitz梯度，因此对k次迭代采用最速下降法，可以表示为：

1.3 对模型的扩展

    式(1)所示高分辨率遥感图像的去模糊模型与传统的去噪模型相似，但又有所不同，主要表现在噪声在一次函数中属于位移的变换操作，如式(1)中对b进行操作，而模糊是其斜率的变换操作，如式(1)中对A进行操作，因此可对其进一步变换：

2 高分辨率遥感图像的去模糊算法

    对高分辨率遥感图像进行去模糊操作，确定算法如下：

    输入：模糊算子A，Lipschitz常数L，观测图像b，归一化参数λ，梯度投影迭代次数K_n，去模糊迭代次数K_b。任一像素x满足l≤x≤u：

    输出：最优化图像x^*。

    第0步：设置：x₀=0；

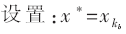
    其中梯度投影操作P_p是由一个矩阵对(p，q)映射到另一个矩阵对(r，s)=P_p(p，q)。

3 模拟实验

    对算法性能进行了测试。“高分一号”获取的遥感图像来自于国家航天局，图像选取北京地区的遥感图像。图1(a)为原始高分辨率遥感图像，图像大小为256×256；图1(b)为经过高斯模糊算子处理以后的图像，模糊算子的标准差为4。实验中设λ=0.000 1，L=2，K_n=1，K_b=2 500。

    实验所使用的PC机是CPU 3.0 GHz，内存为2GB。

    本实验中运用GPA算法实现了对遥感图像的去模糊处理，图1显示了由“高分一号”获取的北京市的遥感图像、经过模糊算子处理以后的模糊图像及GPA算法处理后的效果图。从图中可以看出，本算法能够有效地对模糊遥感图像进行处理，保留更多的细节和边缘信息,改进信噪比ISNR为5.361 4 dB。而参考文献[16]中Elad等人提出的算法的改进信噪比为5.17 dB,因此本算法具有更好的性能。从图1（d）可见，随着迭代次数的增加，该算法能够显著地提高图像的峰值信噪比，更加有利于遥感图像的后续解译及处理。

4 结论

    本文通过对遥感图像进行稀疏表示和快速梯度投影的研究，表明利用快速梯度投影算法能够有效地对高分辨率遥感图像进行去模糊处理。通过对“高分一号”卫星获取的高分辨率遥感图像进行试验，表明对图像稀疏表示后进行快速梯度投影算法去模糊具有更优的效果。另外，本文所提出的遥感图像去模糊算法可以应用在定量遥感研究中和遥感图像超分辨重建中，对该算法的优化和应用的拓展是下一步研究的重点。

参考文献

[1] 秦振涛，杨武年，潘佩芬.基于稀疏表示和自适应字典学习的“高分一号”遥感图像去噪[J].光电工程，2013，40(9)：16-21.

[2] MALLAT S.A wavelet tour of signal processing，3rd ed[M].San Diego，CA.：Academic Press，2008.

[3] CAND?魬S E J，ROMBERG J，TAO T.Robust uncertainty principles: Exact signal recognition from highly incomplete frequency information[J].IEEE Trans. Info. Theory，2006，56(2)：489-509.

[4] DONOHO D.Compressed sensing[J].IEEE Trans. Info. Theory，2006，52(4)：1289-1306.

[5] CANDES E J，TAO T.Near optimal signal recovery from random projections：universal encoding strategies[J].IEEE Trans. Info. Theory，2006，52(12)：5406-5425.

[6] CANDES E J，WAKIN M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine，2008(3)：21-30.

[7] CANDES E J，ROMBERG J.l1-MAGIC：Recovery of sparse signals via convex programming[D].Caltech，2005.

[8] CANDES E J，TAO T.Decoding by linear programming[J].IEEE Trans. Info. Theory，2005，51(12)：4203-4215.

[9] CANDES E J，ROMBERG J，TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Comm. Pure Appl. Math，2006，59(8)：1207-1223.

[10] NESTEROV Y.Gradient methods for minimizing composite objective function[J].CORE discussion paper，no. 76, University of Catholic Louvain, Belgium, Sept. 2007.

[11] NESTEROV Y.Introductory lectures on convex optimization-a basic course[M].Kluwer Academic Publishers, 2004.

[12] RUDIN L，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms[J].Physica D，1992，60：259-268.

[13] DAUBECHIES I，DEFRISE M，MOL C D.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Comm. Pure Appl. Math.，2004，57：1413-1457.

[14] COMBETTES P L，WAJS V R.Signal recovery by proximal forward-backward splitting[J].Multiscale Model. Simul.，2005，4：1168-1200.

[15] BECK A，TEBOULLE M.A fast iterative shrinkage-thres-holding algorithm for linear inverse problems[J].SIAM J.Imaging Sciences，2009，2(1)：183-202.

[16] ELAD M，MATALON B，SHTOK J，et al.A wide-angle view at iterated shrinkage algorithms[C].SPIE (Wavelet XII)2007，San-Diego CA，2007.