摘  要: 从独立分量分析" title="独立分量分析">独立分量分析(ICA)的原理和算法入手,用傅立叶" title="傅立叶">傅立叶和ICA对实际测得的地震灾害救助系统中的声波/振动信号进行分离。从分离的结果看,ICA在复杂信号的分离中更具优越性。 

    关键词: 独立分量分析(ICA)  傅立叶  声波/振动信号  分离

    实际应用中,希望在未知源信号的情况下,从已有混合信号" title="混合信号">混合信号中分离出需要的源信号,为此,人们研究了盲信源分离BSS(Blind Source Separation)方法。盲信源分离是指在信号的理论模型和源信号无法精确获知的情况下,从混迭信号(观测信号)中分离出各源信号的过程。独立分量分析ICA(Independent Component Analysis)是近年来由盲信源分离技术发展来的多道信号盲信源分离方法。对它的研究已成为信号处理领域的一个热点。ICA在本文运用到了一个新的领域——地震救援的声波/振动信号的分离。 

    由于地震后,会有活着的人被埋在废墟中。他们通过各种方式发送信号,希望得到援助。研制开发声波/振动生命探测定位仪的基本目的是发现幸存者的移动、敲击、刮擦和呼喊等表示他们依然活着的信号。技术上,就是通过高灵敏的传感器,探测分析通过固体或空气传播的表示生存的微弱振动信号。 

    对于一个传感器接收的只是一个信号的情况,比较容易处理。但是,当同一传感器接收到不同呼救者传来的信号时,就要对接收的信号进行分离。即把不同的呼救者传来的信号分开,以便通过数学计算,确定呼救者(即振源)的位置(或方向)。 

1 ICA的理论基础 

    噪声的存在使源信号的恢复变得困难,所以应先对混合信号去噪。即根据测量结果,得出在不同介质中传输的信号的频率,进而去掉噪声部分,进行预处理。 

1.1 预处理 

    实际上,独立分量分析是一种优化问题,即如何使分离出的各独立分量更好地逼近各源信号。但它的前提是源信号相互独立,且最多有一个源信号是高斯分布。而实际的观测信号也许并不满足这个要求。基于此,在对观测数据进行ICA处理前,应先对其进行预处理,包括去均值、白噪化。预处理后,使采集的实际信号尽可能满足ICA的前提条件。 

1.2 ICA原理 

    设观测信号X={x₁(t),x₂(t),…,x_n(t)}是未知的相互独立的源信号S={s₁(t),s₂(t),…,s_m(t)}(m≤n)的线性组合,m=n时的ICA的线性组合模型如下面的" title="面的">面的矩阵所示。 

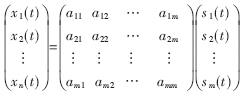
    矩阵中的a_ij(i,j=1,2,…)是未知的模型系数,可描述为: 

    X=AS                                          (1) 

    式(1)中,A是未知的混合矩阵。由(1)式可以得到未知的源信号为: 

    S=A^-1X=W^TX                                     (2) 

    式(2)中,A^-1是A的逆矩阵,W^T为矩阵W的转置矩阵。从该式中,可以清楚地知道,要想求出源信号S,求未知的混合矩阵W是关键。 

    在本文中,因为多个传感器所围成的区域比较小,所以考虑源信号的个数小于等于得到的混合信号个数(m≤n)的情况。当m>n时,可以参考文献[5]。 

1.3 ICA算法 

    本文采用了一种快速定点算法^[1]。该算法通过kurtosis的最大化得到W的学习过程,即: 

    kurt(y)=E(y⁴)-3(E(y²))²                           (3) 

    由此,W的递推公式如(4)式: 

    W(k)=E(X(W^T(k-1)X)³)-3W(k-1)                   (4) 

    具体的算法实现如下: 

    (a)初始化W(0),令‖W(0)‖=1,置k=1; 

    (b)代入(4)式求W(k),其中的期望值可由大量X向量的采样点计算出来; 

    (c)用‖W(k)‖去除W(k); 

    (d)如果|W^T(k)W(k-1)|不是足够接近1,那么置k=k+1,返回至(b);否则,输出向量。 

    本算法最后给出的向量W(k)等于正交混合矩阵中的一列,在信号分离中意味着分离了其中的一个非高斯信号。即W^T(k)X(t),t=1,2,…等于其中的一个源信号。该算法一个显著的特性是迭代次数非常少,一般3～20次(次数用误差矩阵控制)。为了估计n个独立成分,必须运行上面的算法n次。 

2 声波信号的分离 

    原始语音信号如图1,它们的混合信号如图2。 

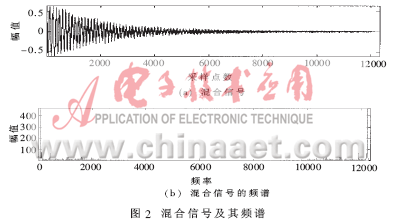
    在图2(b)中,信号的低频和高频部分有比较明显的分界线(虽然也有很少的非主频的混叠),可以用传统的傅立叶对它进行分离。分离的结果如图3。从图3中可看出,结果是可以接受的。但用ICA分离的效果更好,如图4。 

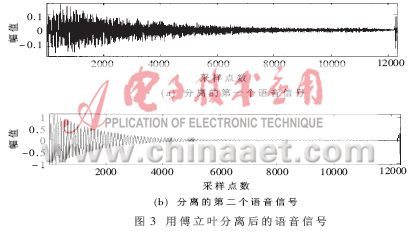
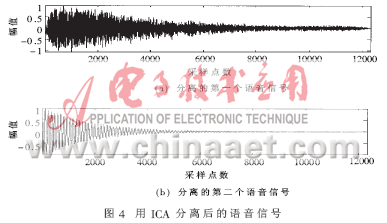
3 振动信号的分离 

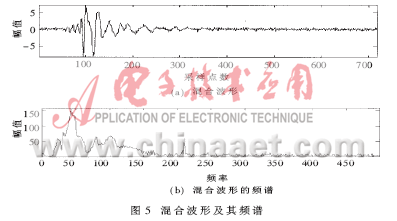
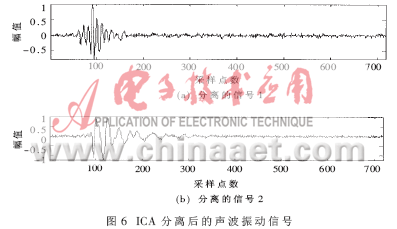
    在实际的采集试验中(以两个振源为例),如果各个呼救者传来的信号间的时间间隔很小,使它们完全混合在一起,就无法轻易地看出混合信号的组成成分,如图5(a)。当然,它们也许在频率域是分开的,所以,对混合信号进行傅立叶变换" title="傅立叶变换">傅立叶变换,如图5(b)。从图5(b)中可知,它们的频谱也是混叠的,用傅立叶变换仍无法分离。因此,处理这种复杂信号,选用ICA。图6是用ICA分离的结果。用ICA分离后的信号进行数学计算,得出的振源位置和实际试验时得出的位置是一致的。 

    ICA对声波/振动信号的实际处理得到了满意的结果。尽管用ICA作信号分离的前提是被分离的源信号必须相互独立,但是它也提供了一种实际信号分离的有效手段。同时,在ICA中,时移信号的分析和源信号的数目大于混合信号的数目等问题,还有待进一步研究。 

参考文献 

1 Hyvarinen  A, Oja  E. A fast fixed-point algorithm for  Independent component analysis[J]. Neural Computation, 1997(9):1483～1492. 

2 周卫东,贾磊,李英远.一种独立分量分析的迭代算法和实验结果.生物物理学报,2002;18(1):57～60。 

3 杨竹青,胡德文.独立成分分析方法在盲源信号分离中的应用.计算机测量与控制,2002;10(3):200～202 

4 李 力,屈梁生.应用独立分量分析提取机器的状态特征.西安:西安交通大学学报,2003;37(1);45～48 

5 S.Shamsunder,G.B.Giannakis. Modeling of non-gaussian  array data using cumulants:DOA estimation of more sources  with less sensors. Signal Processing,1993;30(3):279～297