张延响1,2,3，程学珍1,2,3，杨吉语1,3，李乾1,2,3

　　(1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2.山东科技大学 电子通信与物理学院，山东 青岛 266590；3.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590)

　　摘要：针对智能传感器自校正的问题，构建了基于IEEE1451智能传感器校正引擎的校正模型，优化了校正公式，阐述了曲线拟合法的基本原理。然后以应变式称重传感器为实例，描述了其工作机理，并分析误差产生的原因，以曲线拟合法为理论依据，进行非线性校正。通过实验数据求出校正引擎多项式各项系数，将电压量代入校正公式，进行砝码标定值与校正输出值之间的比较。实验结果表明，利用校正引擎对称重传感器进行校正，实现了称重传感器输入与输出之间的线性化关系，改善了零点漂移的情况。

　　关键词：校正引擎；非线性；称重传感器；曲线拟合

　　中图分类号：TP212.6文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.05.020

　　引用格式：张延响，程学珍，杨吉语，等.基于曲线拟合的智能称重传感器自校正［J］.微型机与应用，2017,36（5）：65-68.

0引言

　　*基金项目：山东省重点研发计划项目（2016GSF117009）由于受到温度、电源交叉敏感参量等问题的影响，传统传感器普遍存在输入输出非线性的问题，这些问题通过电路、材料及工艺改进无法完全解决，往往需要对传感器进行校正［1］。对传感器非线性化的处理可采用硬件和软件补偿的方法［2］，硬件补偿即用硬件电路进行校正，但存在电路复杂、通用性差、成本高等缺点，不利于实际应用；软件补偿是将传感器获取的信息传给计算机，通过软件算法对接收到的数据进行自校正和实时补偿，来提高测量精度。

　　自校正是智能传感器非常重要的功能特点，智能传感器集成了微处理器和通信模块，具有更强的数据处理和通信能力［3］。基于IEEE1451协议［4］的智能传感器，将多个传感器结合成一个传感器单元进行信号处理、模数转换等，侧重于简化传感器连接到现有的控制和传输网络。通过该标准特有的变换器电子数据表格（Transducer Electronic Data Sheet，TEDS）校正引擎可实现多传感信息自校正。虽然该协议给出了校正引擎的数学模型，但没有给出传感器通道模型建立的方法，所以智能传感器校正引擎的关键技术在于校正方法的研究。校正方法的选择需要考虑所需的TEDS存储空间的大小、校正算法所需浮点数的运算次数、校正算法的准确度等方面的因素。

　　本文以称重传感器为例，根据IEEE1451.2标准构建校正模型，利用微处理器数据处理的优越性，运用软件补偿的方法即基于最小二乘的曲线拟合理论，推导校正多项式，搭建校正引擎，进而实现应变式称重传感器的非线性校正。

1校正引擎模型

　　1.1校正模型的构建

　　IEEE1451.2标准定义了校正电子数据表格，这个表格通常存储于变换器接口模块（Transducer Interface Module，TIM）中［5］，通过校正TEDS对传感器通道进行校正和补偿。智能传感器实际工作时，校正引擎先从TEDS读取标定数据，然后进行校正计算。执行传感器数据校正，要先确定测量值所在的分段区间，在校正引擎中选择特定校正方法。

　　IEEE1451智能传感器数据校正模型图如图1所示，网络适配器（Network Capable Application Processor，NCAP）首先获取校正TEDS，然后通过校正引擎来实现传感器校正［6］，即从TEDS中读入校正参数和传感器的实际测量值，并将其转换为实际的输入物理量值［7］，从而体现传感器智能化的特点。

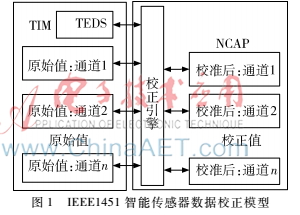
　　1.2校正公式的优化

　　根据IEEE1451标准，TIM中每个通道的校正函数可以用下面的多项式函数表示：

　　f(X1,X2,...,XN)=

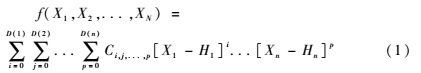
　　式中，Xn表示从传感器的输出值；Hn、D(K)、Ci,j,...p分别表示输入变量的偏移值、阶数和多项式的系数［8］，各个参数均存储在电子数据表格中。

　　为了便于理解，校正公式可以写成如下多项式形式：

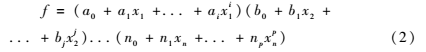
　　其中a，b，… ，n与系数项Ci,j,...p对应，xi则对应［X-H］中各项。IEEE1451智能传感器标准TEDS的每个字段数据格式如表1所示。

　　若直接以式（2）形式进行TEDS配置，则需先对所有多项式系数a，b，...，n及修正系数等进行定义，为每个系数分配字段编号、字段名称、数据类型、数据长度及数据内容。在多项式参数较多的情况下，过多同一类型的字段重复定义，将占用较大的TEDS存储空间。若令：

　　则式（2）可写成如下矩阵函数形式：

　　f(X1,X2,...,Xn)=AX1·BX2·…·NXp(3)

　　这就是以分类矩阵的形式表示的校正公式。系数以矩阵形式进行TEDS数据存储，可以减少对系数的字段序号、字段名称、数据类型、数据长度等重复定义，节省了TEDS的存储空间。校正引擎公式作为校正TEDS的重要组成部分，必须严格按照表1格式进行配置。

　　1.3校正方法

　　基于显式建模的校正方法容易与TEDS标准形式实现统一，TEDS校正引擎模型参数设置须与TEDS格式相适应。曲线拟合法是一种显式建模方法，通常采用n次多项式来逼近非线性曲线，多项式方程的各个系数由最小二乘法确定。曲线拟合法的特点是计算实时性好、技术成熟，能够获得较好的校正函数。

　　假定非线性曲线拟合多项式方程xi(ui)=a0+a1ui+a2u2i+...+anuni，式中xi为标定数据输入，ui为输出，n由所要求的准确度来确定，a0，a1，… ，an为待定常数。根据最小二乘法的原则，即通过选取基函数求得拟合函数f(u)，在点ui处函数值f(ui)逐渐逼近观测点的数据xi，使二者差的平方和达到最小［9］，并将误差平方和最小的问题转化为求极值的问题，从而获得待定系数a0，a1，…，an。

2智能称重传感器自校正

　　2.1应变式称重传感器工作机理

　　应变式称重传感器主要由悬梁臂、电阻应变片及电桥电路构成。电阻应变片是一种传感元件，能将试件的应变转化成电阻值的变化。将电阻应变片粘贴在元件特定表面上，当被测对象受力变形时，应变片也随同变形，进而引起应变片电阻的变化，电阻的变化经电桥作用后输出电压信号［10］。应变式称重传感器测量电路如图2所示，该测量电路由惠斯登全桥和差分放大电路组成，R4、R5起到电桥调零的作用，使用AD620作为仪表放大器进行差分放大。

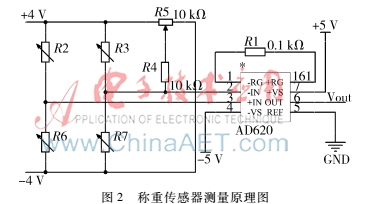
　　2.2误差分析

　　实际测量使用时，应变式称重传感器的输入与输出之间存在非线性误差，其原因主要是：受自身材质的限制，工艺及技术的影响，传感器的非线性因素无法完全消除；在外界温湿度、空气扰动等影响作用下，传感器的零点会发生漂移及灵敏度会产生变化；虽然采用差动电桥可以消除一部分非线性误差的影响，但实际桥臂上电阻的初始值不可能完全对称，因此由同一干扰量引起的阻值改变量均不可能完全相同，导致误差不能够相互抵消［11］；称重传感器输出的信号为差模小信号，其含有较大的共模部分，当差分放大电路对共模信号抑制能力较弱时，共模干扰经过放大电路的放大就会产生较大的误差。

　　因此，要提高称重传感器的测量准确度，需要对其进行非线性校正即通过校正引擎来实现输入与输出之间的线性化。

　　2.3非线性校正

　　非线性校正源于非线性补偿，传感器的输入与输出之间呈非线性关系，通过串联一个补偿环节来实现非线性补偿。该补偿环节是根据曲线拟合法的基本原理，利用最小二乘法的原则，求出符合传感器精度要求的校正引擎多项式，使传感器输入-输出之间呈线性关系［12］。

　　智能传感器具有通过校正引擎对前端传感器进行非线性的自动校正功能。它的突出优点在于不受限于前端传感器及其调理电路至A/D转换的输入-输出特性的非线性程度，仅要求传感器及其调理电路至A/D转换器的输入-输出特性重复性好。

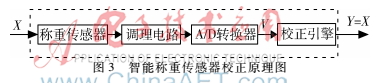
　　智能称重传感器校正原理图如图3所示，X为输入的被测重量，V为传感器输出的电压量。输入量X与传感器输出量V之间的关系可由n阶多项式表示：

　　X=a0+a1V+a2V2+...+anVn+β(4)

　　其中，β为高阶无穷小，a0~an为常系数。

　　根据实际需要令n=3，则式（4）可变为:

　　X=a0+a1V+a2V2+a3V3(5)

　　下面的过程就是曲线拟合的过程，即需要求出a0~a3的值。曲线拟合多项式（5）计算得到Xi与实验标定值Xi之间的误差，设为Δi，则误差平方和为：

　　其中i=1，2，… ，n，n为标定点的个数，使误差平方和取最小值的问题可转化为多元函数：

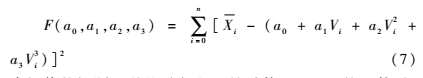
　　求极值的问题。误差平方和F是系数a0~a3的函数，根据多元函数求极值的条件，将F(a0,a1,a2,a3)分别对a0~a3求偏导，并令各偏导数为零，即：

　　可得关于系数a0~a3的线性方程组：

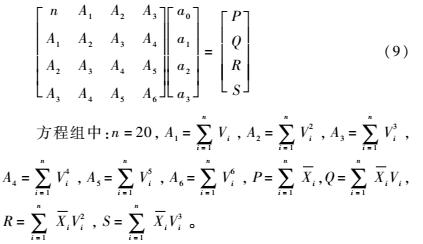
　　通过实验得到标定值Xi以及对应的输出电压Vi，进而求解该矩阵，可得待定系数a0~a3，代入式（5）中即可得校正引擎多项式。

3实验数据分析

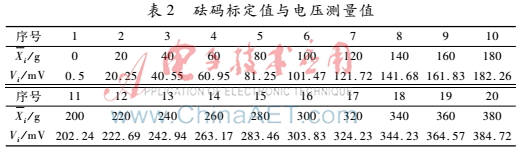
　　按照图2所示电路原理图进行电路设计，获取该称重实验的重量值Xi和输出电压值Vi。先进行调零，然后在传感器托盘上依次放上固定质量的砝码，同时通过测量得到传感器的输出电压，结果如表2所示。

　　由表2中的数据，计算式（9）中相关量的值如下：n=20，A1=3.849×103，A2=1.013×106，A3=2.998×108，A4=9.462×1010，A5=3.111×1013，A6=1.052×1016，P=3.8×103，Q=1.0×106，R=2.961×108，S=9.345×1010。

　　将其代入式（9）中，求出系数a0~a3，其值为：a0=－0.327，a1=0.991，a2=－9.486×10－6，a3=－5.464×10－9。从而求得称重传感器非线性校正的表达式：

　　X=－0.327+0.991V－9.486×10－6V2+5.464×10－9V3(10)

　　式（10）为该智能称重传感器的校正引擎多项式，将表2中输出电压值Vi代入该式中，可得经非线性校正后的输出值，如表3所示。由表3可知，称重传感器经过TEDS校正引擎校正之后，零点漂移为0.17，满量程时相对误差为0.026%。如果测量中需要更高的精度，则提高曲线拟合多项式阶次的值即可，但需要注意的是，阶数的增高将使计算繁冗，运算时间也迅速增加。

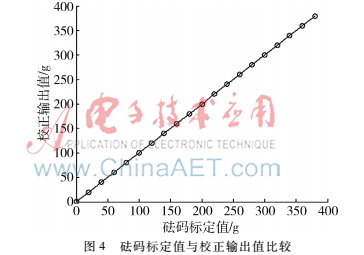
　　校正后砝码标定值与校正输出值之间的关系如图4所示，从图中可以看出所有的点几乎在一条直线上，即输入与输出保持近似的线性关系，说明经过TEDS校正引擎的校正功能，保证了该称重传感器输出的线性化，同时改善了零点漂移的情况。

　　4结论

　　本文将标准校正引擎公式优化成矩阵多项式的形式，减少了TEDS对校正公式系数类型格式的重复定义，节省了TEDS存储空间。针对应变式称重传感器，结合曲线拟合的理论，通过实验数据，得到了符合IEEE1451.2标准的校正引擎多项式，使零点偏差由0.5减小到了0.17，满量程时的相对误差达到了0.026%，实现了称重传感器的非线性补偿，有效地提高了智能称重传感器的测量精度。

　参考文献

　　［1］ 王建武，冯正和. 全相位相位差测量中的系统误差及校正［J］. 系统工程与电子技术，2014，36(9)：1707-1711.

　　［2］ LIU J, XIE X J, HAN H J, et al. Research on the PWSM servo system position on sensor correction［C］. 2012 7th International Power Electronics and Motion Control Conference, 2012: 1324-1327.

　　［3］ 王睿智，史庭训，焦文品. 一种基于元组空间的智能传感器协同感知机制［J］. 软件学报，2015，26(4)：790-801.

　　［4］ KUMAR A, SRIVASTAVA V, SINGH M K, et al. Current status of the IEEE 1451 standardbased sensor applications［J］. IEEE Sensors Journal, 2015, 15(5): 2505-2513.

　　［5］ KUMAR A, KIM M, HANCKE G P. Environmental monitoring systems: a review［J］. IEEE Sensors Journal, 2013, 13(4): 1329-1339.

　　［6］ 吴忠杰，林君，李冶. IEEE1451标准智能传感器中网络应用处理器的实现［J］. 传感器与微系统，2006，25(6)：85-88.

　　［7］ 陈向群，朱伟，杨瑞多. 网络化智能传感器通用开发平台的设计与实现［J］. 仪器仪表学报，2004，25(1)：34-38.

　　［8］ 黄国健，刘桂雄，洪晓斌，等. IEEE1451网络化智能传感器的通用建模方法及应用［J］. 光学精密工程，2010，18(8)：1914-1921.

　　［9］ 陈国栋，刘宏，王江涛. 基于曲线拟合的PEBB单元散热优化设计［J］. 电工技术学报，2016，31(4)：71-77.

　　［10］ 胡玉梅，张方建，邵毅敏，等. 应变片敏感栅结构参数对测量精度的影响［J］. 重庆大学学报，2013，36(12)：21-27.

　　［11］ 景婧. 应变式称重传感器的非线性校正［J］. 计算机应用研究，2013，30(1)：189-191.

　　［12］ 郭伟，张栋，李巨韬，等. 改进型BP神经网络对电容称重传感器的非线性校正［J］. 传感技术学报，2012，25(10)：1354-1360.