超宽带技术以其显著的带宽和优异的时间分辨力，在信道容量和抗多径性能上明显优于目前的窄带通讯技术，从而引起广泛的关注。超宽带技术的高速发展需要对超宽带信号室内传输特性有更深入的了解，所以构建室内模型十分重要。研究超宽带室内信道模型的主要思路在于重点考虑路径损耗、阴影衰落和多径信号的影响。路径损耗和阴影衰落可以综合为关于传输距离的路径损耗模型^[1]，多径影响可以归纳为关于时间的冲击响应模型。而冲击响应模型中，又有将模型的参数以随机变量表示的统计模型^[2~3]、结合射线法和一致性绕射理论(UTD)的确定信道模型^[4]。统计模型基于大量测量数据，着重描述接收信号的时域统计特性；确定信道模型偏向于给出接收端波形的确定解。
　　UTD理论被用于超宽带研究已有较长一段时间，从早期的频域" title="频域">频域模型^[5]一直到最近的时域模型^[6]。文献^[6]应用时域的UTD理论和射线跟踪算法" title="跟踪算法">跟踪算法，实现了对超宽带室内多径的详尽描述，并得到了接收信号不同极化的电场时域波形。本文采用文献^[6]中的时域分析方法，结合本实验室已有的基于射线法的电波传播仿真软件，仿真给定的室内环境，主要研究超宽带信号室内电场强度的分布特点和多径接收带来的效果改善。
1 射线法和时域分析相结合的室内多径仿真模型
　　室内多径环境下，研究的接收信号主要包括直射波、反射波和绕射波。时域的超宽带模型主要描述接收信号的时域特性，特别是波形在传播过程中的形变。对此可以先构建传统的频域模型，经傅立叶逆变换或矩阵方法得到^[5]。但这种方法需要足够的频域信息才能得到尽可能精确的时域解，面对超宽带信号会有计算量大且结果不精确的问题。针对此点，寻找信道的时域冲激响应，直接从时域进行求解将是更有效更精确的解决方案。本文所介绍的仿真模型，重点描述室内环境因素的影响，没有引入收发天线的响应。模型应用反射、绕射的时域反射系数，结合射线跟踪算法分析出的多径信息，得到超宽带信号经室内传播的电场强度，模型具体形式如下：
　　
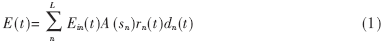
　　(1)式中L是路径总数，n表示某一条路径。接收电场强度E(t)是每路径响应的和，E_in(t)是发射信号电场强度，是发生绕射前的球面波扩散系数，sⁿ是发生绕射前的传播距离。r_n(t)、d_n(t)分别是时域反射系数和时域绕射系数，此路径发生反射或绕射时，描述时域波形的畸变情况。
1．1 时域反射、绕射系数
　　在有损介质中，相对介电常数是频率的函数，所以反射系数与频率有关。对频域反射系数作适当变换，得到时域反射系数^[6]。

1.2 模型仿真结果
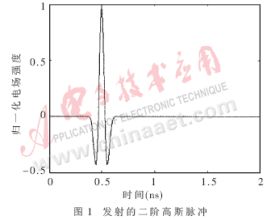
　　将时域分析方法应用于本实验室已有的射线跟踪算法的软件中，对简单情况的室内传播进行仿真。仿真所用时域信号采用二阶高斯脉冲w(t)^[6]。
　　

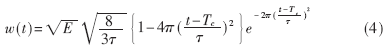
　　(4)式中脉冲宽度τ=0.11ns，波形延迟T_c=0.5ns。脉冲波型如图1所示。

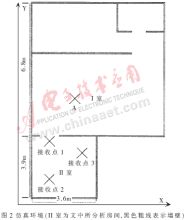
　　仿真环境如图2所示，房间高3m，天花板、地板和墙壁的电参数ε_r=5，σ=0.7。发射信号在I室A点，高2m，垂直极化发射。为计算超宽带信号的室内电场强度分布，在II室沿X、Y方向每隔0.2m设置接收点，每接收点高1.2m，共设置了380点。接收点提取z方向极化的电场强度。图3给出了有代表性的三种情况，分析接收点处时域信号场强相对发射信号的归一化值。如图2所示，接收点1在直射路径可到达的区域，点2在只有反射和绕射路径到达的区域，点3在只有经过绕射和多次反射的路径才能到达的区域。

　　比较图3可以看出，在直射区域，直射路径最先到达，且信号最强，在全部多径信号中占绝大部分能量；没有直射路径时，场强最大信号未必最先到达，其他多径信号所占能量比例增大；在只有绕射和多次反射路径到达的区域，最强路径相对其他路径的信号已没有很大差距，全部接收信号场强非常弱。
2 超宽带信号室内场强分布特点
　　超宽带脉冲信号具有优异的时间分辨力，从而能较方便地提取多径信息，因此可进行多径接收的RAKE接收方案备受关注。RAKE接收机可依据需要调整接收径数，将多径信号能量叠加以改善接收性能。本文计算了超宽带信号室内传播的电场强度分布，分析了获取单径信号时场强与多径信号时场强的区别，为超宽带接收机做多径接收提供参考。为分析超宽带室内电场分布特点，选取接收脉冲的电场强度，所有数据相对发射信号强度归一化。在此基础上，对每个接收点的多径信号选取脉冲场强最大的路径，得到单径接收情况下II室脉冲电场强度分布图，如图4所示。从图4可看出，左上部有通过门的直射路径，接收信号场强最大，达到0.14以上，其次一次反射路径能到达的区域场强较强，剩下的大部分区域以多次反射路径和绕射路径为主，归一化场强在0.02以下。为更好地描述整个区域上的场强分布，笔者做接收点信号场强统计图，如图5所示，横坐标是接收信号归一化场强，纵坐标是达到此场强接收点所占的百分比。
　　从图5看出，在这种仿真环境，单径接收情况下，归一化场强大于0.05的接收点仅占全部的22.6%。半数接收点场强在0.025以下，整体信号很弱。这是因为天线设置在房间外，房间内直射范围很小，大部分点接收的都是多次反射和绕射路径。
　　为了在多径环境下改善系统性能，将不同路径的接收信号累加起来，利用多径现象提高总的接收信号强度。下面分析多径接收对室内覆盖性能的改善。所用方法是将最强几径信号的电场强度模值直接相加，旨在比较多径接收带来的变化，结果如图6所示。

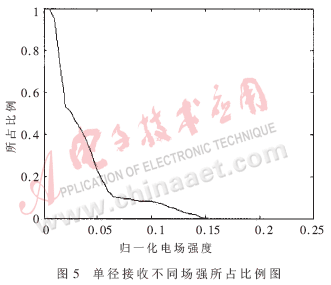
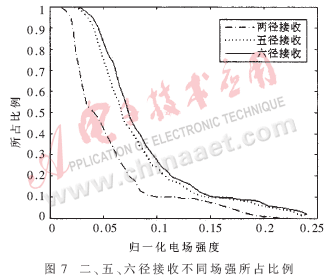
　　图6是两径接收时在每个接收点叠加最强两径场强的分布图。与图4比较可以看出，多径接收对室内信号覆盖性能有较大改善。图7给出了二、五、六径接收时接收场强统计图。两径接收时归一化场强大于0.05的接收点达到42.37%，改善接近一倍；五径接收时，较单径和两径已有明显提高，归一化场强大于0.05的接收点达到75.8%，大于0.1的接收点也达到24%，整个房间的信号覆盖性能得到很大提升；观察六径接收的结果，归一化场强大于0.05的接收点达到83.7%，大于0.1的接收点达到27.6%。比较五径接收效果的改善，六径接收带来的提高就相对有限，当继续增加径数时这一现象也更为明显。随着接收径数的增加，接收机复杂度也会相应提高，所以适当选取接收径数可达到接收效果与接收机复杂度的综合最优效果。
　　本文介绍了一种射线跟踪与时域分析结合的仿真模型，并用此模型仿真了给定布局的室内环境。从仿真结果看，模型能较准确地描述接收信号的时域特征。对给定布局的室内环境中一个房间的信号场强分布进行了分析，针对RAKE接收机可接收多径信息的特点，比较了多径接收对信号覆盖性能的影响。仿真结果表明，一定程度的多径接收能明显改善室内信号覆盖。本文所得结果对超宽带室内通信具有参考意义。
参考文献
1 S. Ghassemzadeh, R. Jana, C.Rice,W.Turin, V. Tarokh.A Statistical Path Loss Model for In-Home UWB Channels. 2002 IEEE Conference on Ultra Wideband System and Tech-nologies, May 2002:59～64
2 UWB Channel Modeling Contribution from Intel. IEEE P802.15 Working Group for Wireless Personal Area Networks
3 M.Z. Win, D. Cassioli. The Utral-Wide Bandwidth Indoor Channel: from Statistical Model to Simulation. IEEE Journal on Selected Areas in Communications,2002;20(6):1247～1257
4 Bernard Uguen, Eric Plouhinec, Yves Lostanlen, Gérard Chassay. A Deterministic Ultra Wideband Channel Modeling. 2002 IEEE Conference on Ultra Wideband System and Tech-nologies, May 2002:1～5
5 Mark McClure, Robert C. Qiu, Lawrence Carin. On the Su-perresolution Identification of Observables. IEEE Transactions on Antennas and Propagation,1997;45(4):631～641
6 Richard Yao, Grace Gao, Zhengqi Chen, Wenwu Zhu.UWB Multipath Channel Model Based on Time-Domain UTD Tech-nique. Global Telecommunications Conference 2003 (GLOB-COM′ 03), IEEE,2003;3(12):1205～1210
7 Paul R.Rousseau, Prabhakar H. Pathak.Time-Domain Uni-form Geometrical Theory of Diffraction for a Curved Wedge. IEEE Transactions on Antennas and Propagation, 1995;43(12):1375～1382