1引言

随着半导体器件的发展，电力电子装置的大量应用，导致大量谐波电流涌入电网，污染电网，这一问题已引起了各国的重视。为了限制总的谐波含量（THD）以提高功率因数，制定了许多标准，如IEC100032。近年来，如何提高功率因数成为了电力电子领域研究的热点，提出了许多有源PFC电路[1]～[3]。有两种功率因数校正方案，其一是采用控制输入电流使其接近正弦，这种方案中电路工作在连续导电模式(CCM),通常要求双闭环控制，由于对输入电流、电压及输出电压取样，这种方案比较复杂，成本高，限制了该方法的使用[4]～[5]。另一种方案是采用电压跟随（VoltageFollower）方式[6]，电路通常工作在不连续导电模式(DCM)，开关由输出电压误差信号控制，这种PFC方案仅需要一个电压控制环，这种方案相对简单，引起了研究人员的广泛关注[6]～[8]。

本文通过对工作于DCM的普通Cuk变换器功率因数校正能力的分析，给出了提高其功率因数校正能力的方案，同时使器件应力得到降低。在传统的CukDC/DC变换器中，两个电感存在依赖关系，即它们同时进入DCM或CCM，通过在电路中加一二极管，改变了它们之间的依赖关系，使它们可以独立工作于不同的导电模式。因此，在利用电压跟随方法进行功率因数校正时，令输出电感工作于CCM，而输入电感工作于DCM，从而减小了输出电压纹波，提高了变换器的效率。

2工作于DCM的CukAC/DC变换器的功

率因数校正能力

传统的CukAC/DC变换器如图1所示，当其工作于DCM时，其输入电流波形如图2所示，从图2可以得到，在一个开关周期TS内，输入电流iin的平均

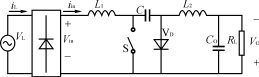
图1传统的Cuk变换器

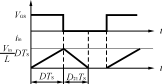
图2输入电流iin的波形

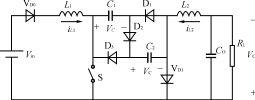
图3改进的VFPFCCukDC/DC变换器

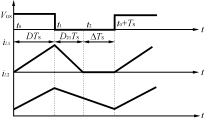
图4变换器的主要波形

值为：=(D＋D21)TSVin/L1（1）

由式（1）可以看出，由于D21的存在，与Vin不是线性关系，D21越小，与Vin越接近线性关系，从而变换器的功率因数校正能力越强。由电感的伏秒平衡可得：

VinDTS=(VC－Vin)D21TS（2）

从而D21=D（3）

从式（3）可以看出，欲减小D21从而提高变换器的功率因数校正能力，可以通过增加VC得以实现。本文提出经改进的Cuk变换器，通过一开关电容网把储能电容分成两个大小相等的电容，它们串联充电，并联放电，从而提高了变换器的功率因数校正能力，现分析如下：

在传统的Cuk变换器中，假设电容C上的电压为VC，则其储藏的能量为CVC2/2，现由两个大小为C/2的电容C1、C2储藏相同的能量，设电容C1、C2上的电压均为VCS，则：CVC2=C1VCS2＋C2VCS2=CVCS2（4）

从上式可以看出，VCS与VC相等，但电容C1、C2是串联于电路中的，其上的电压之和为2VC，这相当于提高了式（3）中的VC，从而提高了Cuk变换器的功率因数校正能力。

3改进的CukDC/DC变换器

在传统的CukDC/DC变换器中，输入与输出电感具有相互依赖关系，即它们同时进入DCM或CCM。为解除这种依赖关系，在传统的CukDC/DC变换器中引入了一二极管VD0,在所提出的CukDC/DC变换器电路中，用一开关电容网代替储能电容C，从而提高了变换器的性能。图3为所提出的CukDC/DC变换器电路，在此基础上，提出了一种新的PFC电路。

在讨论新的PFC电路之前，首先分析图3所示的电路，为简化分析，作如下假设：

（1）电路工作进入稳态；

（2）所有元器件是理想的；

（3）开关频率fs远大于输入电压频率f，在每个

开关周期，输入电压保持恒定；

（4）电容C1、C2、C0足够大，其上的电压保持恒定。

图3所示的电路中，电感L1工作在DCM模式，电感L2工作在CCM模式，其主要的波形如图4所示，这时，电路有三种工作状态，分析如下：

模式1（t0≤t

模式2(t1≤t

模式3(t2≤t

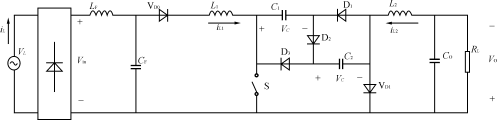
图5改进的VFPFCAC/DC变换器电路

电感L2继续给负载电容C0，负载电阻RL提供能量，iL2线性下降.

当电感L1工作在DCM,电感L2工作在CCM时，根据伏秒平衡原理可知电容上的电压为：

VC=(D＋D21)Vin/2D21（5）

输出电压为

VO=DVC=(D＋D21)DVin/2D21（6）

4改进的VFPFCCukAC/DC变换器的

电路分析

图5为所提出的VFPFCCukDC/DC变换器电路，图中LF,CF组成高频滤波网络，由于开关频率远大于输入交流电压频率，可以假设在一个开关周期TS内，输入电压保持不变。

定义输入电压为：

vin(t)=|Vpsinωt|（7）

式中：Vp为输入电压的峰值；

ω为输入电压的角频率。

由于在提出的变换器中，要求电感L1工作在DCM，而电感L2工作在CCM，故需知道它们工作在临界状态时的值，现推导如下：

在模式1，流过电感L1的电流iL1可表示为：

iL1(t,t′)=Vpt′|sinωt|/L1(0iL1p(t′,t)=VpDTS|sinωt|/L1（8）

式中：TS为开关周期；

D为开关S的占空比；

t′为时间坐标，其原点为每一个开关周期中开关导通的时刻。

由伏秒平衡原理可得：

VinDTS=(2VC－Vin)(1－D－Δ)TS(9)

由于要求电感L1工作在DCM，只需要保证输入电压vin(t)达到最大值时L1工作在DCM的边界，此时由伏秒平衡原理可得：

VpDTS=(2VC－Vp)(1－D)TS

(VC－VO)DTS=VO(1－D)TS（10）

把式（7）、式（10）代入式（9）可得：（11）

在一个开关周期内电感电流iL1的平均值可表示为：

〈iL1(t)〉=iL1P(t,t′)(1－Δ)/2

=VpDTS(1－Δ)|sinωt|/2L1（12）

把式（9）代入式（10）可得：〈iL1(t)〉=（13）

上式就是改进的VFPFCCukAC/DC变换器电路的输入电流表达式，在半个输入电压周期电源的输入功率为：（14）

式中：平均输出功率为：

Pout=VO2/RL=D2VP2/4RL(1－D)2(15)

假设变换器的效率为η，根据功率平衡原理可得：

ηPin=Pout(16)

即=（17）

由上面的分析可得，输入电感L1工作的临界值为：L1=（18）

下面推导电感L2工作的临界值，由于输出功率

Pout=〈iL2〉VO（19）

电感L2工作在CCM与DCM的临界条件时，在一个开关周期TS内，流过电感L2的平均值〈iL2〉为：

〈iL2〉=iL2P/2=(VC－VO)DTS/2L2（20）

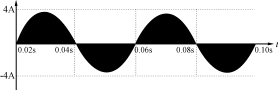
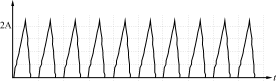
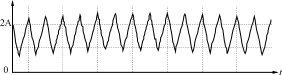
图6电路的仿真波形

(a)输入电流iL的波形(b)电流iL1的波形

(c)电流iL2的波形

由式（19）、式（20）可得：

Pout=(VC－VO)DTSVO/2L2

=VP2D2TS/8L2(1－D)（21）由式（15）、式（21）可得电感L2工作的临界值为：L2=（22）

只要电感L1的值小于其临界值，而电感L2的值大于其临界值，则可以保证输入电感L1工作于DCM，从而实现了VFPFC的功能，而输出电感L2工作于CCM，从而减小了器件的应力和输出电流纹波。

5仿真结果

设计要求如下：输入电压vin(t)=110sinωt,电源频率f=50Hz，输出电压VO=127V，输出功率PO=200W（RL=80Ω），开关频率fs=100kHz。仿真所选的参数为：输入电压vin(t)=110sinωt,其频率f=50Hz，输入电感L1=100μH，输出电感L2=1000μH,开关频率fs=100kHz，开关的占空比D=0.45。仿真的波形如图6所示。图6(a)为输入电流iL(t)的波形，由图可见，输入电流的包络线近似为正弦波，仿真得到的输入电流功率因数为0.995。图6(b)为电感L1上的电流iL1的波形，电感L1工作在DCM。电感L2工作于CCM，流过L2的电流波形如图6(c)所示。

6结语

在传统的CukDC/DC变换器中引入一个二极管，改变了其输入与输出电感之间的依赖关系。通过对输入电感工作于DCM的Cuk变换器的功率因数校正能力的分析，用一开关电容网代替原单个储能电容，从而提高了其功率因数校正能力。通过对所提的VFPFCCukAC/DC变换器的分析，找出了输入与输出电感工作的临界值。在所提出的变换器中，输入电感L1工作于DCM，以实现功率因数校正，输出电感L2工作于CCM，从而减小了器件应力和输出电流、电压纹波。MATLAB仿真与实验结果证实了理论分析的正确性。