摘要：PID控制是过程控制中应用最广泛的控制方法，其关键在于PID参数的优化。针对其参数整定和优化问题，提出了一种改进的粒子群优化算法。仿真结果证明了该算法的有效性，其性能优于遗传算法和基本微粒群算法，具有一定的工程应用前景。
关键字：粒子群算法；PID控制器；克隆选择；参数优化
Application of an improved PSO algorithm in PID parameters optimization
Shao hui-feng
(Oxygen Factry,Tonggang Iron&Stell Inc.Tonghua134004,Jilin,P.R.China)
Abstract：PID control is the most common control method used in process control, and the core technology lies in the optimization of the PID parameters. An improved particle swarm optimization is proposed in tuning and optimization of PID parameters in this paper. Simulation results verified the effectiveness of improved PSO and show that its performance is better than GA algorithm and base PSO, which means a well prospective.
Key words：Particle swarm algorithm; PID controller; Clone selection; Parameter optimization
1 引言
PID控制器结构简单，对模型误差具有鲁棒性和易于操作等优点，问世半个多世纪以来在各个控制领域中得到了广泛的应用。PID控制器是按偏差的比例（P）、积分（I）和微分（D）通过线性组合构成控制量，对被控对象进行控制。这三个参数整定的好坏不但会影响到控制的质量，而且还会影响到控制器的鲁棒性。因此对PID控制器参数整定的研究成了人们关注的重要问题之一。
随着PID参数整定技术的不断发展，人们提出了各种各样的整定方法。常规的方法一般是基于模型或者基于规则的自整定，随着智能算法的发展人们提出了一系列的PID自整定方法，如基于模糊规则[1]，基于神经网络[2]以及遗传算法[3]的自整定方法等等。
微粒群优化（Particle Swarm Optimization , PSO）算法具有算法简单易实现的优点，已经被应用于众多工程领域。本文将在原有算法的基础上提出一种改进的微粒群算法，将其应用于PID控制器的参数整定中。该算法克服了传统PID控制器参数寻优的不足，仿真结果表明该算法优于遗传算法的基本微粒群算法。
2 PID控制器描述

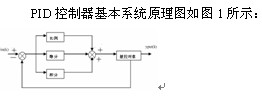
图1 模拟PID控制系统原理框图
3 算法描述
3.1 基本微粒群优化算法
微粒群算法（particle swarm optimization,简称PSO）是Eberhart和Kennedy等人模拟鸟类的捕食行为于1995年提出的一种新的全局进化优化算法[4]。基本原理是：将优化问题的每个解作用一个粒子，每个粒子在n维空间中以一定的速度飞行，并通过一定的适应度函数来判断粒子位置的优劣，每个粒子根据自身的飞行经验以及群体的飞行经验来调整自己的飞行状态，向空间中的更优位置飞行。粒子自身经过的最优位

3.2 改进微粒群优化算法
PSO算法具有概念简单、易于实现、具有较强的全局收敛能力和鲁棒性等优点，但是它同时也具有智能群体算法的固有缺陷容易陷入局部最优。为了克服粒子群算法的缺点，我们引入克隆免疫机制构造一种克隆免疫粒子群算法。免疫算法（Immune Algorithm, IA）是受到免疫系统启发而发展起来的一类仿生算法，该算法主要是模拟自然界生物免疫系统的机理和功能而实现[5]。克隆选择算法是免疫算法中基于克隆选择学说而提出。由于克隆选择算法中存在着选择，克隆以及变异操作可以保证解的多样性。
本文的做法是在粒子群算法外部建立一个规模为初始粒子个数1/10的最优解集m。每当粒子群算法出现一个新的全局最优解 我们就将其加入到最优解集中,替换最优解集中适应度最小的解，使最优

定义3：选择算子，用经过柯西变异后产生的粒子直接代替当前的所有粒子。
克隆免疫粒子群算法与基本微粒群算法不同的时，它在原有微粒群算法基础上加入了克隆免疫操作。当粒子群算法陷入局部最优时，对外部最优解集中的粒子进行克隆复制，克隆变异和克隆选择操作，提高了粒子的多样性，帮助算法跳出局部最优解，避免早熟收敛，提高了解的精度。

3.4 克隆免疫粒子群算法的PID参数优化步骤
应用克隆免疫粒子群算法实现PID控制器参数优化的算法流程如下：


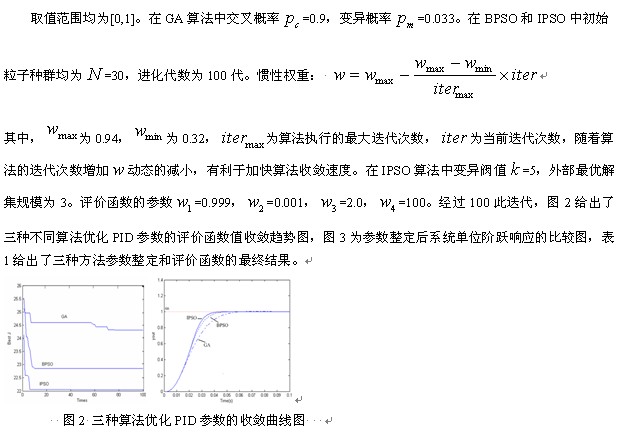
图3 三种算法阶跃响应曲线图

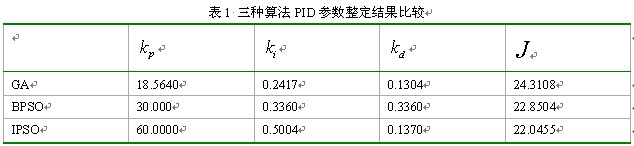
从图2、图3以及表1可以看出：收敛速度、搜索能力以及在系统响应时间上改进的微粒群算法都要优于基本微粒群算法和遗传算法。
5 结论
本文基于克隆选择算子提出了一种改进的粒子群算法，其收敛速度和精度都优于遗传算法和基本微粒群算法，并有效避免了算法容易陷入局部最优的缺点。将其应用于PID参数整定，通过仿真实验证明了算法的可行性和有效性。
参考文献
[1] Linc, Xu J X，Hang C C, Comparison between a fuzzy PID controller and a kind of nonlinear PID controller[C]. Proc 36th IEEE Int Conf On Decision and Control S Diego(CA),1997.
[2] 张世峰，李鹏.基于神经网络的自整定PID参数控制器设计[J].自动化仪表，2009，30（7）：64-66.
[3] 周志，干树川.基于遗传算法的控制参数优化研究[J].计算机应用，2007，27：191-192.
[4] Kennedy J, Eberhart RC. Particie swarm optimization[C]. In: Proc.of the IEEE Int’1 Conf on Neural Networks. Perth: IEEE Inc, 1995: 1942-1948.
[5] Dasgupta D. Artificial Immune System and Their Applications. [M]. Springer-Verlag, 1999
[6] 刘金琨. 先进PID控制MATLAB仿真[M]. 第2版. 北京：电子工业出版社，2004:223-228.