摘 要： 提出了一种快速二维最大相关准则阈值分割算法。该方法利用积分和迭代编程技术，避免了数据的重复运算，从而将计算的复杂性从一般二维最大相关准则方法的O(L⁴)减少至O(L²)。实验结果表明，该方法分割效果好，计算效率高，适合实时图像系统的应用。
    关键词： 阈值分割；最大相关准则；快速算法

    阈值化是图像分割中一项重要的技术^[1]。常用的阈值分割方法有：直方图双峰法、最大熵法、矩量保持法、梯度统计法、一维最大相关准则法^[2]，以及这些方法在二维上的推广化方法。这些方法中，一维最大相关准则以其运算简单、分割效果好、适用范围广而得到广泛应用。
    一维最大相关准则法由Yen^[3]等人提出。该方法以图像的一维直方图为依据，以目标和背景的相关总量为最大选择阈值，在多数情况下能取得很好的阈值。但在实际应用中，当图像信噪比降低时，应用一维最大相关法将产生很多分割错误。为此，2005年陈修桥^[4]等人将一维最大相关法(MCC)推广到二维。二维最大相关法应用二维直方图，不仅反映了灰度分布信息，还反映了邻域空间相关信息，使分割效果得到了明显改善。但其计算量大、耗时长，难以实用。为了解决这一问题，本文利用积分和迭代编程技术，实现了算法的简化，减少了计算复杂度，增强了算法的实用性。
1 二维最大相关准则阈值分割
    若一幅图像的灰度级数为L，总的像素点数为N(m×n)，设f_ij为图像中点灰度为i、区域灰度均值为j的像素点数，p_ij为点灰度-区域灰度均值对(i，j)发生的概率，即：
   
其中，N（m×n）为图像的总像素数，则p_ij{i，j=1…L}就是该图像关于点灰度－区域灰度均值的二维直方图。
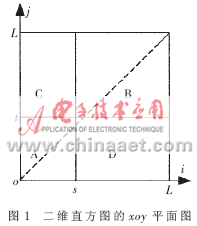
    图1为二维直方图的xoy平面图。沿对角线分布的A区和B区分别代表目标类和背景类，远离对角线的C区和D区分别代表边界和噪声，所以应该在A区和B区上利用点灰度－区域灰度均值，通过二维最大法确定最佳阈值，使真正代表目标类和背景类的相关数为最大。这两类的分别被定义为：
   
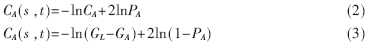
其中：
   
相关数的判别函数定义为：

2 快速二维最大相关准则阈值分割算法
    在上述二维最大相关准则阈值分割算法中，对于每个(s，t)对，都要从头开始计算P_A(s，t)和G_A(s，t)，运算过程是一个四重循环，计算复杂性为O(L⁴)，计算比较耗时。实际应用中，为了提高运算速度，减少重复运算，需进一步优化算法。
    从式（2）、式（3）和式（7）可以看出，计算TC(s，t)需要计算P_A(s，t)、G_A(s，t)和G_L。而G_L恒定，P_A(s，t)是二维直方图P中坐标(s，t)左上方的元素和，G_A(s，t)是p²_ij形成的矩阵G中坐标(s，t)左上方的元素和。
    根据以上分析，如果能够找到一种快速计算二维矩阵中坐标(s，t)左上方元素和的方法，则必然能够避免二维相关准则算法中点的重复计算。本文针对二维直方图P和矩阵G分别进行一次积分迭代操作：
   
其中，l(s，t)表示二维直方图P中纵坐标t列元素和；P_A(s，t)是二维直方图P中坐标(s，t)左上方的元素和，且l(s，1)=0，P_A(-1，t)=0；ls(s，t)表示矩阵G中纵坐标小于等于t的列元素和，G_A(s，t)表示矩阵G中坐标小于等于(s，t)左上方的元素和，且ls(s，1)=0，G_A(-1，t)=0。
    通过这样优化，该算法可将计算的复杂性减少到O(L²)，从而大大减少了计算的复杂性，提高了计算速度。具体实现算法如下：
    (1)由原始图像计算各像素点的领域平均灰度值，从而形成二维灰度直方图。
    (2)赋初值：
    max=0，l(s，-1)=0，PA(-1，t)=0，ls(s，-1)=0，G_A(-1，t)=0，s∈[0，L]，t∈[0，L]
    (3)找出最佳阈值向量(S，T)：
    ①根据式（9）和式（10）计算矩阵P_A(s，t)和G_A(s，t)，s∈[0，L]，t∈[0，L]
    ②按式（2）、（3）计算C_A(s，t)和C_B(s，t)
    ③按式（7）计算TC(s，t)
    if (TC(s，t))>max
    { max=TC(s，t)；S=s；T=t}
    (4)利用阈值向量(S，T)分割图像原始图像，可得分割结果。
3 实验结果与分析
3.1 基准测试图像分割实验
    实验是用Matlab 6.5语言在P42.4GB、内存512MB的微机上进行。选用经过噪声污染的Lenna图像（图片大小为256×256，灰度级256）进行分割，比较一维最大相关准则阈值分割法、二维最大相关准则阈值法和本文快速算法的差异，得出实验分割结果如图2所示，它们的图像分割阈值与运行时间见表1。

    从图3(a)可以看出，基于一维最大相关准则分割法分割效果差，图像中仍然存在一些噪声颗粒，光截曲线不能清晰检测，不利于后续处理和测量；对比图3(a)、图（b）和图(c)可以看出，基于二维最大相关准则法分割和本文算法分割结果几乎相同，分割效果明显优于一维最大相关准则阈值分割法，光截曲线检测清晰。
    从表2可以看出，本文算法分割阈值接近二维最大相关准则阈值分割算法，运行时间比二维最大相关准则算法也节约99%左右。
    二维最大相关准则阈值分割法和本文算法不仅考虑了孤立像素点的灰度信息，而且还充分利用了像素的空间邻域信息，抑制噪声能力大大加强，分割错误明显减少。利用一种积分和迭代编程技术快速计算二维最大相关准则函数，大大减少了算法的复杂度，提高了算法的实用性。实验结果表明，本文算法是一种效率高、分割效果好的阈值分割算法，具有较好的应用前景。
参考文献
[1] SEZGIN M.Survey over image thresholding techniques and quantitative performance evaluation.Journal of Electronic Image[J].2004，13(1)：146-165.
[2] 韩思奇，王蕾.图像分割的阈值法综述.系统工程与电子技术[J]，2002，24(6)：91-94.
[3] YEN J C，CHANG F J.A new criterion for automatic multilevel thresholding[J].IEEE Trans on Image rocessing，1995，4(3)：370-378.
[4] 陈修桥，胡以华.二维最大相关准则图像阈值分割递推算法.计算机工程与应用[J]，2005，32：91-93.