摘  要： 在时延和频移两个方向上，对跳频信号的模糊函数进行了分析，提出了一种基于跳频信号模糊函数自项特征的时频表示方法。其核函数在信号的模糊域能够有效地滤除噪声和交叉项，并保留绝大部分的自项能量。仿真试验结果证实，与平滑伪维格纳分布相比较，该方法提高了信号项的时频聚集性，具有更好的参数估计性能。 

    关键词： 跳频信号； 核函数； 参数估计； 模糊函数

    跳频信号具有很强的抗干扰和抗截获能力，一经出现便在军事通信中得到了广泛的应用。作为典型的非平稳信号，其频谱随时间快速变化。传统的傅立叶分析不能有效描述跳频信号的频率变化，而时频分析从时间和频率两个维度上描述了信号的能量变化，因此，时频表示成为跳频信号分析的有力工具。 

    应用比较广泛的时频分析方法，是信号的双线性时频表示。为了在保持时频分辨率的同时，有效抑制交叉项，众多的学者对此展开了深入研究，产生了类型众多的时频表示方法^[1]。由于跳频信号的非线性调频性质，其交叉项干扰尤为严重。平滑类维格纳分布SPWVD(Smoothed Pseudo-Wigner Distribution)在时间和频率两个方向对信号的维格纳分布实现平滑，极大地抑制了交叉项的影响^[2-3]；另外，SPWVD分布核函数形状简单、与信号时频结构关联不大，从而得到了广泛研究^[4-7]。1997年，Barbaross^[5]首次将维格纳分布引入跳频信号的参数估计中，它采用时域平滑的方法抑制交叉项，并给出了粗略的参数估计算法。在信噪比大于6dB情况下得到了准确的跳频周期。张朝阳等^[6]提出在时频域平滑的平滑伪维格纳分布来同时抑制时频两个方向上的交叉项，可以在信噪比大于4dB时得到跳频驻留时间和跳频时刻的有效提取。参考文献[7]将重排SPWVD方法应用于跳频信号分析，实现在0dB时提取信号驻留时间以及跳变时刻。但是，平滑方法在抑制交叉项的同时，降低了信号的时频分辨率，重排算法又使运算量急剧增加，都无法满足实际应用中对跳频信号参数估计的需求。 

    本文首先建立跳频信号模型，然后针对跳频信号模糊域特征，提出一种新的时频分析方法，并与SPWVD方法做了比较，指出其优越性。 

1 Cohen类二次型时频表示 

    信号x(t)的Cohen类时频分布统一表示为： 

    积分区间在(-∞,+∞)，其中A(τ,v)是信号的模糊函数，定义为: 

    Φ(τ,v)为时频分布的核函数，决定着不同的时频分布及其属性。实际应用中，信号属性差别很大，对时频特征的要求也不尽相同，固定核函数很难满足信号时频分析要求^[1]，而自适应方法的运算量又比较大^[8-9]；客观上要求针对具体应用，结合信号分析要求的时频属性，对核函数进行设计。本文基于跳频信号模糊平面分析，结合参数估计的具体应用，提出了一种新的时频表示方法。 

2  跳频信号模型及其模糊函数分析 

2.1 跳频信号模型

    跳频信号x(t)可以看作一个单音脉冲信号x₀(t)时频移位的结果，即: 

其中，是宽度为T_H的矩形窗，T_H为跳频周期，f_k是跳频频率，αT_H是跳变时刻。 

    在本文的分析中，假设跳频信号的参数与参考文献[6]类似。观测时间为8个跳频周期，跳频频率f_k依次为{5,45,20,10,35,15,25,40,30}Hz，采样率为f_s=100Hz，跳频周期T_H=0.32s，跳变时刻αT_H=TH/2。 

2.2 跳频信号的模糊函数 

    把(3)式代入(2)式中，得到跳频信号的模糊函数表示： 

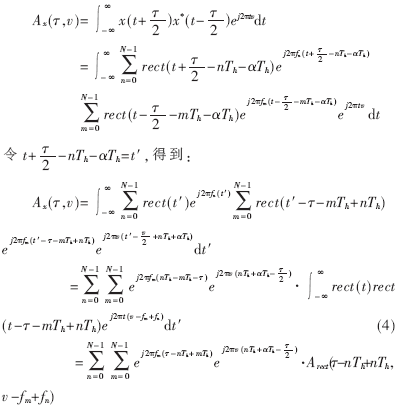
（定义下同）的模糊函数，即： 

    由（4）式可以看出，随机跳频信号的模糊函数是由A_rect(τ,v)按照一定规律经过时移、频移后加权叠加而成的，形成平行于τ轴的带状结构。在时延方向上模糊带的中心间隔相同，为T_h，频率方向上的间隔由于跳变而呈现一种随机性。 

    当m=n时，模糊平面中心附近由N个子脉冲的A_rect函数叠加而成，构成信号的自项部分，即: 

    由此可见，跳频信号模糊函数的自项由子脉冲模糊函数加权得到，在频移方向上具有抽样函数形式。结合式（5）可知，其主瓣宽度在原点处具有最小值，随着时延的增加（远离模糊平面原点）而增加，呈现“哑铃”状，其中主瓣中心窄，两端宽，而旁瓣分布在“哑铃”的两个侧向，沿着频移方向无限延伸，其等高线见图1，尽管由于频率的随机性使得等高线不连续，但是其形状仍然具有上述特点。 

3 核函数设计 

3.1 核函数 

    由第二节可知，跳频信号模糊函数自项在时延方向上的宽度为跳周期，频移方向上表现为抽样函数形式，其主瓣宽度随着时延的大小而改变。根据式(1)模糊域的时频表示可知，“理想”时频表示要求信号模糊函数与核函数要尽量匹配，在抑制信号互模糊带的同时，使自模糊带尽可能通过，因此，提出一种新的时频核函数，定义为： 

其中,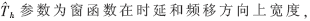c是一常数，控制着信号自项的扩展程度，取值应满足聚集性和交叉项抑制的要求，一般应小于最小跳频频率间隔。 

3.2 参数设计 

    设计核函数的性能与参数有关。由式（4）可以看出，跳频信号模糊平面各带在频移方向上的距离等于跳频频率间隔，实际跳频通信系统中，不仅各个跳频频率各不相同，而且必须满足一定的频率间隔。因此，尽管跳频频率具有随机性，但是互模糊带不可能位于时延轴上，距离时延轴的最小距离由跳频频率的最小间隔决定。由此，可以搜索窗函数宽度的合适值：首先计算跳频信号的模糊函数，然后在频移中心位置，沿着时延方向搜索幅值变化得到自项的宽度，即。 

4  仿真实验结果 

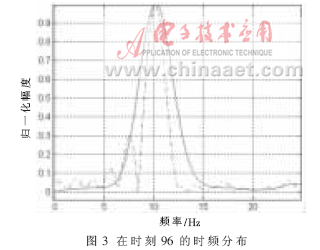
    图2给出了SPWVD分布的核函数以及设计核函数的等高线图。与图1信号模糊函数的自项相比较，设计核函数在形状上与信号自项更为匹配：主瓣沿着频移方向较窄而在时延方向较宽，从而更好地在抑制交叉项的同时保留自项能量。图3给出了在时间抽样等于96时两种时频分布的时频聚集性表示，可以明显看出新核函数比SPWVD具有更窄的主瓣宽度。

    通过在信号中加入不同信噪比的高斯白噪声，在-10dB～+15dB范围内对每个信噪比做500次实验，求出跳频信号参数估计的性能曲线（参数估计算法参见文献[6]），见图4。从图中可以看出，在频率估计方差基本相同的情况下，跳周期估计的信噪比阈值降低了1dB，而且随着信噪比的增加，各个参数的估计方差比SPWVD都相应减小，证明了算法的有效性。

    由于跳频信号频率变化的非线性，二次型时频表示具有严重的交叉项干扰。基于跳频信号模糊域自项分析，本文提出了一种新的时频表示方法。该方法在抑制交叉项的同时可以保留尽可能多的自项能量。与SPWVD方法相比，基于新核函数设计的跳频信号时频分析具有更高的时频聚集性，应用于信号参数估计具有更好的性能。 

参考文献 

[1] COHEN L. Time-frequency  distributions-A review [J].Proc. IEEE, 1989,(77):941-981. 

[2] FLANDRIN P. Some features of time-frequency representations of multicomponent signals[C].Proc. IEEE 1984 internat. Comf.Acoust. Speech Signal Processing (ICASSP84), San Diego, CA, March 1984, 41B:1-4. 

[3] FLANDRIN P, MARTIN W. Pseudo-wigner estimators for the analysis of nonstationary processes[C]. Proc. IEEE  Spectr. Est. Workshop II, Tampa, FL,November 1983: 181-185. 

[4] HLAWATSCH F, MANICKAM T G. Smoothed pseudowigner distribution, Choi-Williams distribution, and conekernel representation: Ambiguity-domain analysis and  experimental comparison[J]. Signal Processing, 1995,43:149-168. 

[5] BARBAROSSA S. Parameter estimation of spread spectrum   frequency hopping signals using  time-frequency distributions[A]. First IEEE Signal Processing Working on Signal Processing Advances in Wireless Communications. 1997：213-216. 

[6] 赵俊, 张朝阳,赖利峰,等. 一种基于时频分析的跳频信号参数盲估计方法[J]. 电路与系统学报,2003,8(3):46-50. 

[7] 张曦, 杜兴民, 朱礼亚.基于重排SPWVD的跳频信号参数提取方法[J]. 计算机工程与应用, 2007,43(15):144-147. 

[8] HENRY K K, JONES D L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform [J]. IEEE transactions on signal processing,2000,48(10):2964-2972. 

[9] STANKOVIC L, KATKOVNIK V. Algorithm for the in stantaneous frequency estimation using time-frequency distributions with adaptive window width [J]. IEEE Signal Process. Lett， 1998,5(9):207-223.