控制系统是制导炸弹的关键部位。目前，所有制导炸弹的控制系统都是基于一定的数学模型，以固定的方式修正弹道误差。由于存在各种不可预知的误差因素，但控制方式却不可调整，造成制导炸弹的实际命中精度不高。针对这种情况，文献[1]提出一种基于自适应神经模糊推理系统(A NFIS)的制导炸弹智能控制系统。它不基于数学模型，通过A NFIS对训练数据的学习来进行控制。由于充分利用了神经网络的自学习能力和泛化功能，并且结合了模糊系统的启发式搜索能力，因而基于ANFIS的智能控制系统具有较高的控制精度和较强的泛化能力。但经过大量实验发现，由于ANFIS不具有抗噪声能力，当训练数据受噪声影响时，必须人工分析数据特征，修改训练数据，才能获得恰当的推理规则，这使得该系统的“智能”性能大打折扣。基于此，提出了一种新的制导炸弹智能控制系统，该系统引入具有前置滤波特性的非单点模糊化技术，针对非单点模糊推理系统内部参数不易调整的问题，提出用梯度下降算法和遗传算法构成的混合并行学习算法调整系统内部参数，从而能够自动处理受噪声影响的训练数据，提高命中精度。通过计算机仿真试验，并与基于ANFIS的制导炸弹智能控制系统进行比较，验证了该控制系统的有效性。

1 非单点模糊推理系统(NSFIS)
    提出的制导炸弹智能控制系统的核心是非单点模糊推理系统(NSFIS)。一个n输入1输出的模糊推理系统，其模糊规则可表述如下
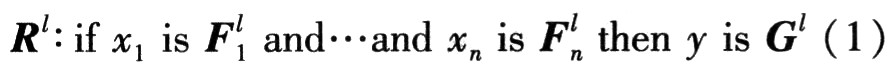
 上的模糊集合，和y∈V对应于系统输入和输出变量，l=1，2，…，M为模糊规则数。
    当采用中心平均模糊消除器、乘积推理规则、高斯隶属度函数和非单点模糊化时，得到的非单点模糊推理系统为

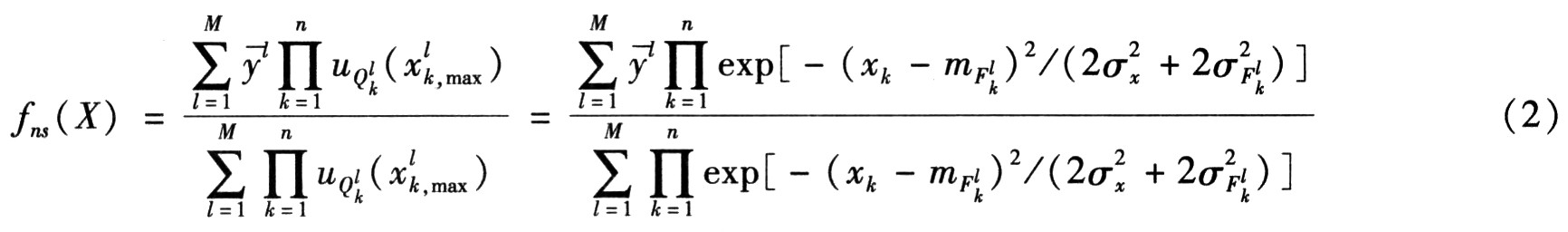
    时，非单点模糊化与单点模糊化等价；当输入变量xk受到噪声污染时，噪声在非单点模糊器中会被因子所克服。如果σx≥σFkl，噪声将会在很大程度上被抑制。

2 NSFIS的参数学习算法
    模糊推理系统是高度非线性系统，在对复杂系统建模的过程中，其内部参数主要依靠某种学习算法对输入一输出数据对进行训练来确定。目前，用于模糊推理系统的学习算法主要是梯度下降算法和递推最小二乘算法。梯度下降算法简单易行、运算量小，但收敛速度慢，容易陷入局部极值，且对信号的谱性依赖较大；递推最小二乘算法收敛速度很快，对信号谱性无依赖，但其结构复杂、运算量大且存在长期数值稳定的问题。从工程的角度考虑，因为非单点模糊推理系统的计算复杂度本身就较大，所以运算量大的递推最小二乘算法不适合采用。为了弥补梯度下降算法的缺点，文中引入遗传算法。遗传算法是模拟生物进化过程的一种全局优化搜索算法，其目标函数既不要求连续，也不要求可微，仅要求问题可计算，而且它的搜索始终遍及整个解空间，容易得到全局最优解。用梯度下降算法和遗传算法同时并行的搜索解空间，并定期交换信息。这样不仅避免了陷入局部极值的缺点，而且加快了收敛速度。虽然由于遗传算法的加入，运算量增加了，但由于遗传算法和梯度下降算法并行工作，所以没有降低算法的实时性。采用减法聚类的方法设置初始参数，进一步加快了算法的收敛速度。文中所设计的非单点模糊推理系统参数学习算法如下：
    步骤1：设置初始参数。采用减法聚类算法对训练数据[X，y]进行聚类处理，得M到个聚类中心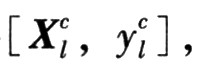构造非单点模糊系统初始参数：选取聚类中心向量Xlc中的各个分量元素作为式(2)中相应的初始值；以与最近的另一个聚类中心欧式距离的一半作为式(2)中作为式(2)中相应的初始值；已知训练数据含有大量噪声的情况下，取
    步骤2：(1)采用梯度下降算法调整参数(推导过程省略)。

 

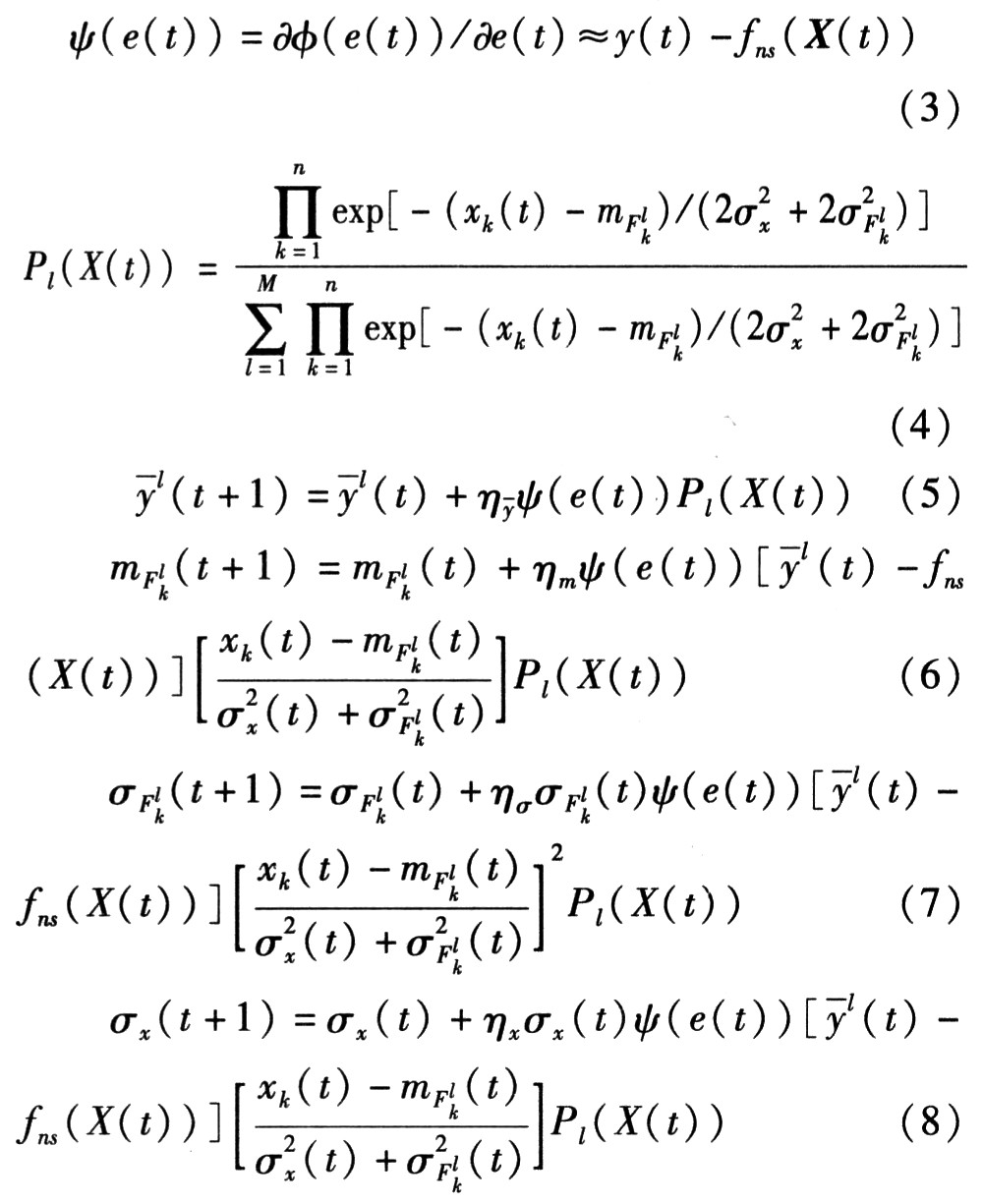
    (2)同时采用遗传算法搜索最佳参数
    1)对参数编码。以减法聚类确定的初始参数值为参考，考虑参数的解空间在初始参数值的正负s倍范围内，将解空间转换为二进制，对各参数进行交叉组合编码；
    2)随机生成20个个体作为初始群体；
    3)将准则函数的数学期望E[φ(e(t))]映射为适应度函数
   
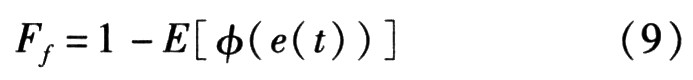
    用该适应度函数对群体中个体的适应度进行评估，当适应度达到标准Ff,max时，进化停止；
    4)遗传操作：采用适应度比例方法进行选择，两点交叉方法进行交叉，采用基本变异算子进行变异。

    步骤3：梯度下降算法和遗传算法之间的信息交换。遗传算法每进化q代，根据准则函数的数学期望E[φ(e(t))]比较遗传算法和梯度下降算法所得参数的效果。若遗传算法搜索到的参数更好，便用其作为梯度下降算法下一步运算的初始参数；若梯度下降算法得到的参数更好，便用其替代遗传算法的当代群体中适应度最差的一个个体。
    步骤4：当准则函数的数学期望E[φ(e(t))]达到标准1-Ff,max时，或者遗传算法进化g代时，算法停止。文中用准则函数在训练数据时间长度内的时间平均代替其数学期望进行运算。

 

3 基于NSFIS的制导炸弹智能控制系统的仿真设计
    按照文献[1]的设计思想，在仿真环境中采用NSFIS设计制导炸弹智能控制系统。
3．1 仿真环境的设定
    假设以下的仿真环境：
    (1)综合风速UZ方向在水平面内，且为常矢；
    (2)重力加速度为9．8 m／s2，无阻尼；
    (3)弹翼可产生的最大调控加速度max a(t)(max a(t)=maxax(t)+maxay(t))随下落高度增加，且不考虑弹翼产生的加速度a(t)在铅垂方向的分量；
    (4)高度H为7 075．4 m(即下落时间T为38 s)，按每0．25 s落下距离△h划分高度空间为N=152层；
    (5)轰炸方式为水平轰炸；
    (6)控制过程不考虑时延；
    (7)弹体运动为质点运动。
3．2 炸弹运动方程的分析
    根据文献[9，10]，水平轰炸的俯视图，如图1所示。

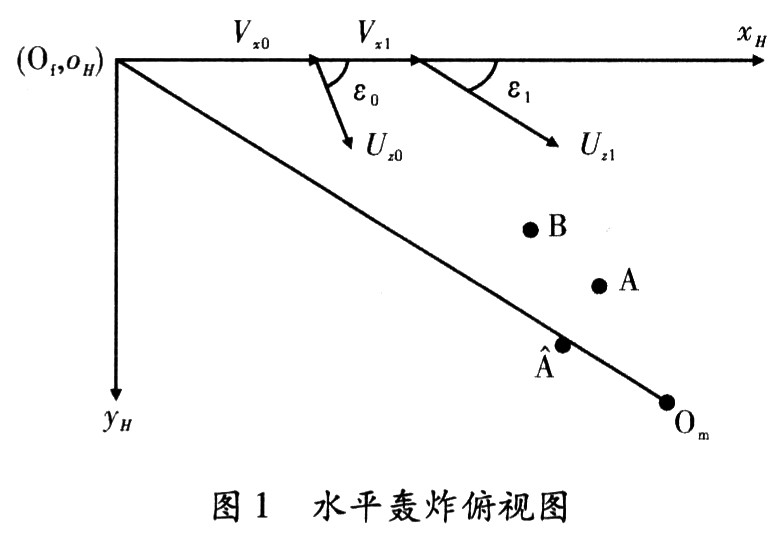
    (oyxz)H：飞机航向坐标系；Of：飞机投弹点；Om：地面目标；A：无需调控，可直接命中弹D0在t时刻的坐标位置；A：需调控，方可命中弹D1在t时刻的坐标位置；B：需调控，方可命中弹D1在t-1时刻的坐标位置。
    无需调控，可直接命中弹D0参数：Vx0：投弹点飞机空速；Uz0：投弹D0时的综合风速；ε0：Vx0与Uz0的夹角；Xh(t)：t时刻弹在xH方向的坐标位置；Yh(t)：t时刻弹在yH方向的坐标位置。
    需调控，方可命中弹D1参数：Vx1：投弹点飞机空速；Uz1：投弹D1时的综合风速；ε1：Vx1与Uz1的夹角；Axe(t)：t时刻和t-1时刻弹在xH方向的位移差；Aye(t)：t时刻和t-1时刻弹在yH方向的位移差；Exh(t)：t时刻弹与目标Om的距离在xH方向的分量；Eyh(t)：t时刻弹与目标Om的距离在yH方向的分量；Vxh(t)：t时刻弹的速度在xH方向的分量；Vyh(t)：t时刻弹的速度在yH方向的分量。Axe(t)：t时刻弹D1和弹D0的位移差在xH方向的分量；Aye(t)：f时刻弹D1和弹D0的位移差在yH方向的分量。在仿真环境中，推导出弹D1在t时刻的运动方程

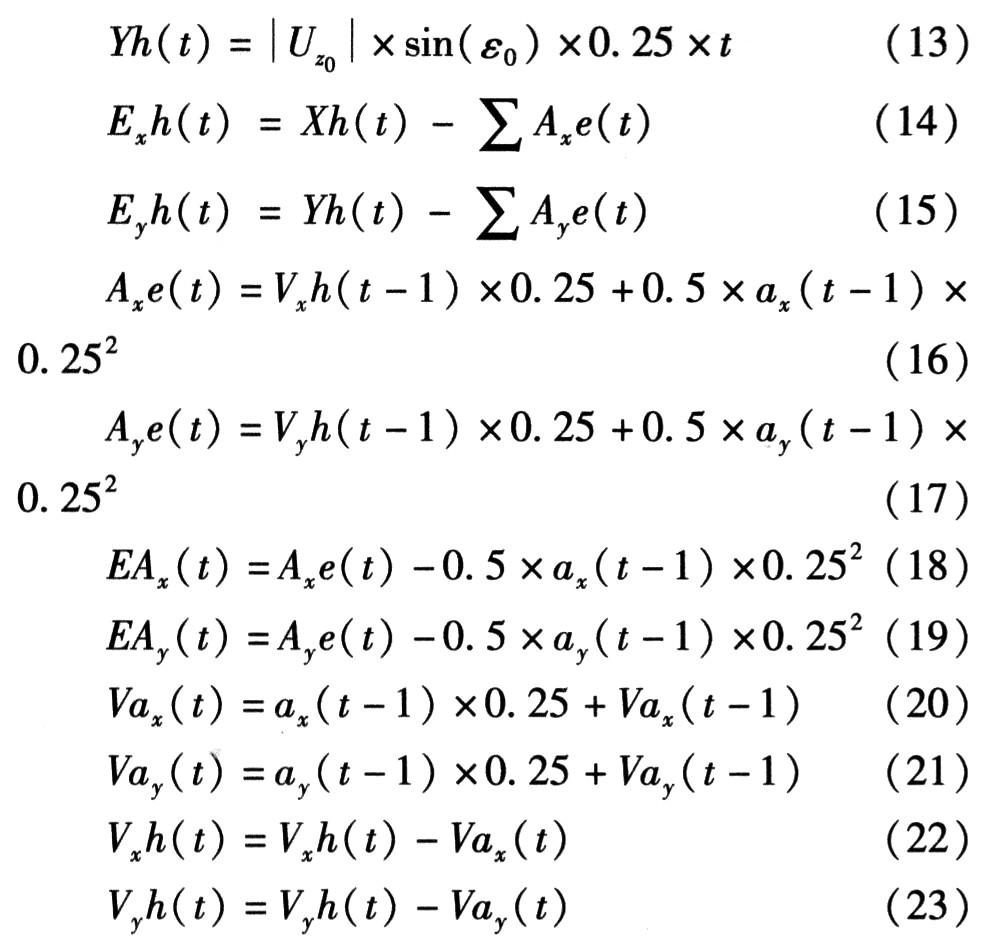
    其中，Vax(t)为xH方向上t-1时刻加速度在时刻生成速度，Vay(t)为yH方向上t-1时刻加速度在t时刻生成速度。

3．3 制导炸弹智能控制系统的建立
    根据弹道运动方程，x与y方向的控制相互独立(a(t)=ax(t)+ay(t))，所以对空间每一层建立两个非单点模糊子系统(NSFISix和NSFISiy)：NSFISix调控导弹在x方向的运动轨迹，输入为Exh(t)、Axe(t)、Vxh(t)，输出为ax(t)；NSFISiy调控导弹在y方向的运动轨迹，输入为Eyh(t)、Aye(t)、Vyh(t)，输出为ay(t)。充分搜集每一层的训练数据，利用文中提出的学习算法调整好NSFISix和NSFISiy的内部参数，就构成了基于NSFIS的制导炸弹智能控制系统，其概略流程图，如图2所示。

 

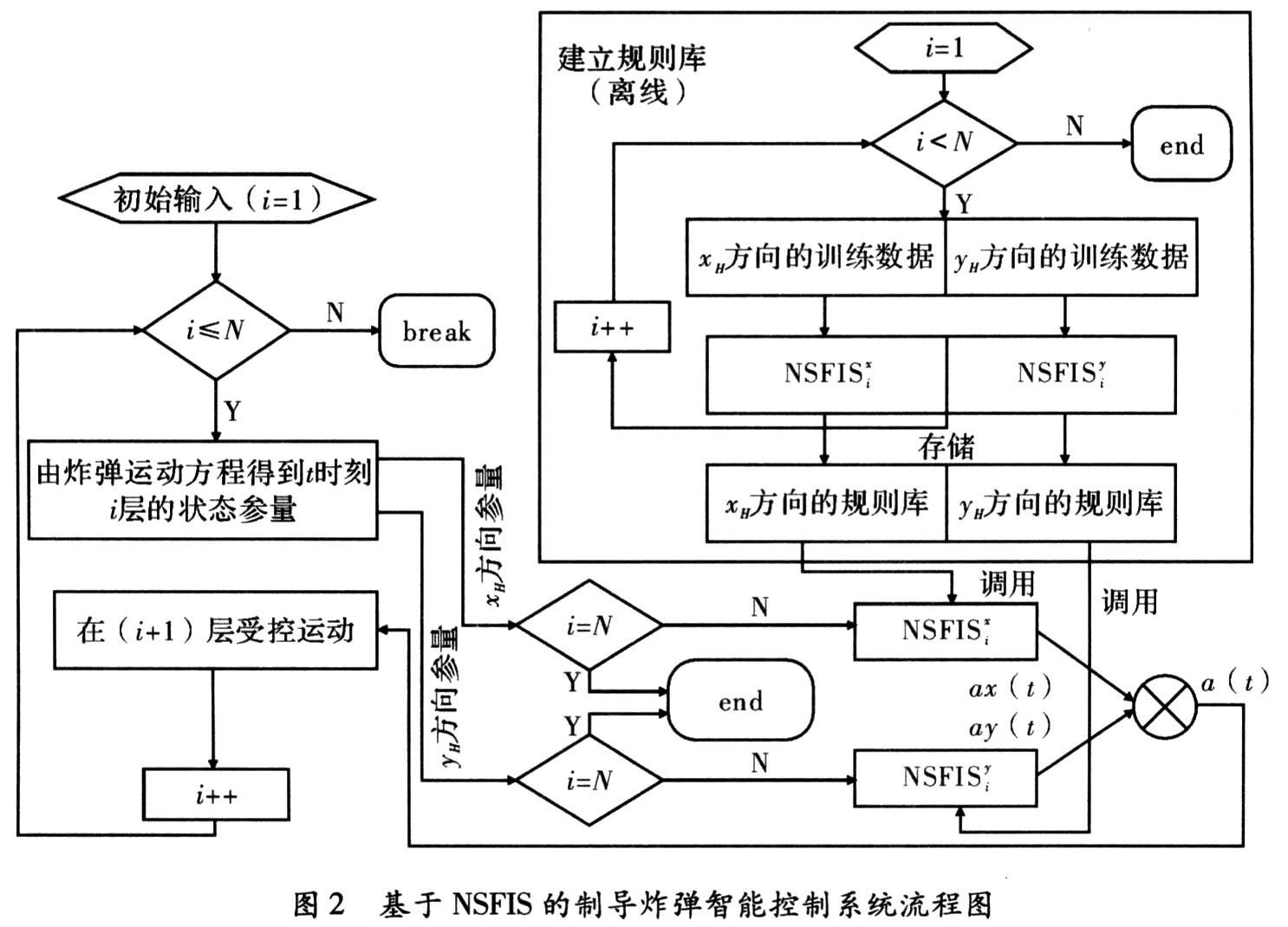
3．4 训练数据的获取
    首先，采用如下算式解算a(t)

弧度，|Uz1|=28、29、30、31 m／s，|Vx1|=319、320、321、322 m／s，ε1=0．3、0．4、0．5、0．6弧度；通过调节参数cx、cy，得到64组圆概率误差CEP∈(4，5)m的训练数据，并对其加入一定程度的扰动误差。
3．5 检验
    设两种投弹初始条件：
    (a)|Uz1|=30 m／s，|Vx1|=321 m／s，ε1=0．5弧度(经训练的投弹初始条件，即教师知识)；
    (b)|Uz1|=30．8 m／s，|Vx1|=319．7 m／s，ε1=0．38弧度(未经训练的投弹初始条件，即非教师知识)。
    用含有扰动误差的训练数据，对基于ANFIS的制导炸弹智能控制系统和基于NSFIS的制导炸弹智能控制系统分别进行训练，并分别在(a)和(b)条件下进行投弹控制试验。设得到两种智能控制系统的控制结果比较如表1所示(表中数据为CEP，单位：m)。

    从表1可以看出，无论在(a)还是(b)条件下，基于NSFIS的智能控制系统控制的命中精度都很高，而基于ANFIS的智能控制系统命中精度很低。这是因为ANFIS不具有抗噪声能力，在训练的过程中，将扰动也作为经验进行了学习，因此其推理误差必然较大，控制不准确。而NSFIS具有较强的抗噪声能力，在学习过程中能够去除扰动影响，因此其控制精度高。现实中，扰动是不可避免的，所以基于NSFIS的制导炸弹智能控制系统具有更高的工程应用价值。

4 结束语
    针对基于ANFIS的制导炸弹智能控制系统不具有抗噪声能力的缺点，文中以非单点模糊推理系统为核心设计了一种新的制导炸弹智能控制系统。利用了非单点模糊推理系统的前置滤波特性，并提出用梯度下降算法和遗传算法构成的混合并行学习算法调整系统内部参数，解决了系统内部参数动态自适应调整的问题。试验结果证明，在训练数据含有噪声的情况下，基于NSFIS的制导炸弹智能控制系统能够自动滤除噪声，实现高精度控制。这对制导炸弹智能控制系统的工程实现具有一定的意义。