摘  要: 针对基-2 FFT处理算法,采用分块存储思想,将存储器、处理机数据交换网络模型进行优化。优化后的网络模型数据通路数仅为20,降低为原来的4%以下,且不随FFT计算点数增多而增加。整个设计在Virtex系统芯片XCV800上实现。 

    关键词: 实时信号处理;并行计算;FFT;网络模型 

    实时信号处理系统^[1]广泛应用于图像处理、语音处理、智能仪表、通信以及自动控制等领域。FFT/DFT作为数字信号处理(DSP)系统中常用的积分变换算法被普遍使用。同时FFT运算的计算量很大,往往构成实时信号处理的计算瓶颈。本文以空间太阳望远镜的相关跟踪系统为研究背景^[2],考虑我国可应用到航天环境的高可靠性的电子系统其主频往往不高于25MHz,所以采用并行计算的策略。通过对计算资源与速度的平衡分析,选择在FPGA内构造两个蝶形处理器实现并行计算。两个处理机采用共享存储器模式^[3]。如果在存储数据与处理机之间采用传统数据总线方式,需要总线仲裁器对总线的请求进行分时应答,难以实现数据从源节点到目标节点的实时传输;而采用点对点任意连接的网状结构会使设计复杂度大幅增加。因此,本文针对FFT运算特点,设计了存储器与并行机的网络模型。该网络模型没有数据传输延迟,但结构得到了极大简化。 

1 并行FFT结构分析 

    本文针对32×32点序列的图像进行FFT变换。可以采用行列变换的形式,对于每行/列数据可以用基-2算法^[4]进行计算。基-2算法计算的核心为蝶形运算。为了实现并行处理,在FPGA内部构造出两个蝶形运算模块,结构如图1。 

    图1中RAM为FPGA块存储器,存放原始数据和FFT之后的最终结果。“Base-2 Core”为蝶形运算单元,图中为两个蝶形运算单元并列构成双核结构,其中每个蝶形运算单元的输入和输出都是两个数据通道。Input Buffer是存储器与蝶形运算单元之间的数据缓存,它逐行接收从存储器RAM发来的数据,然后按一定顺序发送给两个处理单元,并缓存中间结果。Output Buffer为输出缓存,它将FFT最后一级的计算结果进行缓存,等待主存储器RAM空闲时再发送过去。 

2 处理机与存储器网络模型 

    双核处理器的数据输入和输出都是4个通道,每个通道均为复数形式的18位浮点数据(共计36位宽度)。4个通道同时工作意味着有相对应的4个并行的存储器通道。而输入序列是存储在输入缓存中的两行/列共64点数据。如果输入缓存采用FPGA内部的Block Ram方式实现,则难以实现4个通道同时工作。因为32点的基-2FFT共分5级运算,每一级运算请求的数据顺序不同,即使构造4端口的存储器也无法实现同时读取任意4个数据。如果用FPGA内部的查找表(LUT,Look Up Table)实现分布式存储,则存储器与双核处理器组成的网络结构如图2。 

    图2中上方的圆形区域代表存储的数据,下方的圆形区域代表双核处理器的4个通道。如果每个数据都可能进入双核处理器的每一个输入端,则数据通路如同图2的网络结构。假设上方的数据点数为M,下方的数据通路为N,则连接复杂度计算公式为: 

其中,P为通路个数,不同方向表示不同的通路,即公式中的系数2。对于本文情况,数据点M为64,计算通路N为4,所以连接复杂度为512。 

3 基于P_N算子的网络模型简化 

    在基于FFT的蝶形运算中,并非所有数据都有进入任何数据通道的可能性,而是按照一定的规律顺序进入4个计算通道。根据并行FFT算法,并行FFT可以表示为如下递归形式^[5]: 

其中,x_i为第i级变换;C为和差算子;为旋转因子的乘积运算;P_N为完全混合算子。其中C和的作用是完成蝶形运算,而P_N的作用是将数据进行重排。因此可以根据数据重排规律进行网络优化。 

    P_N算子的作用是将序列(a,b,c,d)转化为序列(a,c,b,d)。假设输入序列和输出序列均转化为二维形式: 

    这样完全混合算子的作用相当于矩阵的转置。因此设计上既不采用FPGA内部Block Ram设计输入缓存,也不用分布式存储方法,而是利用分块存储的方式。假设将存储器分为4块,则基于完全混合算子的数据读写方式如图3所示。 

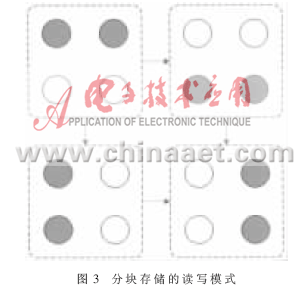
    图3中圆形区域表示存储的分块,4个存储区域构成一个缓存整体。为了实现矩阵的转置,将读和写的控制分开,读取序列为上半区和下半区,写入序列为左半区和右半区。图中实心圆形为活动存储单元,空心圆形为非活动存储单元。图中上两个矩形分别代表读取的两种模式,下两个矩形则代表写入的两种模式。通过读取和写入的不同实现了序列的转置。图3中同时只有两个存储区域活动代表双核处理器的一个计算单元,即两个计算通道。另外两个计算通道情况相同。基于以上设计模型,实际的数据连接模型如图4。

    图4中,上面8个圆形为存储区域,下面4个圆形为计算通路。根据建模分析所有的连接情况如图中的网络,其中箭头代表方向。该图形左右对称,分别代表两个相同的处理单元。它们之间的交叉线表示在FFT最后一级运算时存在数据交换。经初步分析,优化后的网络模型的数据复杂度仅为20。这样通过将输入缓冲存储器划分为8个模块后,可以使设计的复杂度减少25.6倍,即降低为原来的4%以下。而且,随着计算点数的增加,网络的规模保持不变。根据这种方法得到单处理器和多处理器的复杂度如表1所示。 

4 实验结果 

    根据优化模型分别设计相应的输入缓存Input Buffer和输出缓存Output Buffer。分别对这两个单元进行控制信号仿真,仿真波形见图5、图6。 

    图5、图6中“rl”为行列变换转换控制信号。对于输出缓存,“we”和“en”分别为写和读控制信号。可以看出,在行变换和列变换的状态下,分别对应16次读写信号。整个FFT的时间可以从缓存的工作状态估算出来,即190μs～300μs之间,约110μs。 

    对于32×32点的二维FFT,每行/列变换需要分为5级运算,每次蝶形运算同时有4个数据到达。因此完成一次二维FFT共需要32×32×2×5/4=2 560个时钟周期。工作在25MHz的主频下,计算时间约为102μs。估算时间与仿真波形时间相近,可见整个计算过程中数据交换不存在网络延时。 

    综上所述,在FPGA片内实现并行计算时,存储器采用FPGA内的“Block RAM”很难满足多通道数据计算的需求,而分布式存储模式则随FFT计算点数增多而消耗过多资源。通过对特定FFT算法进行分析,改为分块式存储,将网络模型进行了简化,使存储单元与处理器之间的数据通道数缩减为20,并且不随FFT计算点数的增多而增多,将资源消耗控制在一定规模以内。整个并行FFT计算在Virtex XCV800上实现,经测试,计算时间仅为110μs,符合设计需求。 

参考文献 

[1] 苏涛,何学辉,吕林夏,等.实时信号处理系统设计[M].西安:西安电子科技大学出版社,2006 

[2] 布朗,施密特.空间太阳望远镜评估研究报告[M].中国科学院北京天文台,1997. 

[3] 曾泳泓,成礼智,周敏.数字信号处理的并行算法[M].长沙:国防科技大学出版社,1999. 

[4] 胡广书.数字信号处理[M].北京:清华大学出版社,1997.