基于FPGA的FIR滤波器的实现
2009-02-25
作者:郭继昌 向 晖 滕建辅 李香萍
摘 要: 提出了一种采用现场可编程门阵列器件FPGA并利用窗函数法实现线性FIR数字滤波器硬件电路的方案,并以一个十六阶低通FIR数字滤波器电路的实现为例说明了利用Xilinx公司XC4000系列芯片的设计过程。设计的电路通过软件程序进行了验证和硬件仿真,结果表明电路工作正确可靠,能满足设计要求。
关键词: FPGA FIR数字滤波器 窗函数 全加器
随着微电子技术的发展,采用现场可编程门阵列FPGA进行数字信号处理得到了飞速发展。由于FPGA具有现场可编程的特点,可以实现专用集成电路,因此越来越受到硬件电路设计工程师们的青睐。本文研究了基于FPGA的FIR数字低通滤波器硬件电路的实现方法。用这种方法实现的滤波器内部电路结构透明化,并减小了体积,提高了工作效率。
1 用窗函数法设计线性相位FIR滤波器的方法
任何数字滤波器的频率响应H(ejω) 都是ω的周期函数,它的傅立叶级数展开式为: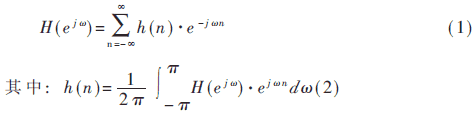
傅立叶系数h(n)实际上就是数字滤波器的冲激响应。获得有限冲激响应数字滤波器的一种可能方法就是把式(1)的无穷级数截取为有限项级数来近似,而众所周知的吉布斯现象使得直接截取法不甚令人满意。
窗函数法是用被称为窗函数的有限加权序列{w(n)}来修正式(2)的傅立叶系数,以求得要求的有限冲激响应序列hd(n),即有:
hd(n)=h(n)·w(n) (3)
w(n)是有限长序列,当n>N-1及n<0时,w(n)=0。
这里我们仅以冲激响应对称,即h(n)=h(N-1-n) (n=0,1,2,…,N-1)时低通滤波器为例进行说明。低通滤波器的频率响应函数H(ejω)如式(4)所示。
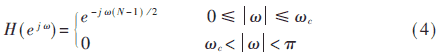
其中,ω为对抽样频率归一化的频率,ωc为归一化截止频率。
利用反傅立叶变换公式求出与式(4)对应的冲激响应h(n),如(5)式所示。
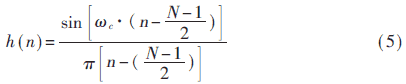
选用汉宁(Hanning)窗作为窗函数,函数如式(6)所示。
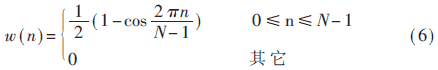
2 十六阶FIR低通数字滤波器硬件电路设计
下面以一个十六阶FIR低通滤波器为例说明硬件电路的设计方法和过程。
2.1 设计指标和参数提取
2.1.1 设计指标
采样频率:≥1.25×106/S 精度:δmax≤±1
截止频率:37.5kHz
类 型:低通 输入数据宽度:8位
阶 数:16阶 输出数据宽度:16位
2.1.2 参数提取
采用上面介绍的低通滤波器的频率响应函数和汉宁窗函数进行设计。计算出的符合设计指标的线性相位16阶FIR数字低通滤波器的特性参数如下:
h[0]=h[15]=0.000000 h[1]=h[14]=0.001992
h[2]=h[13]=0.008241 h[3]=h[12]=0.018332
h[4]=h[11]=0.030784 h[5]=h[10]=0.043353
h[6]=h[9]=0.053550 h[7]=h[8]=0.059257
2.2 单元电路设计
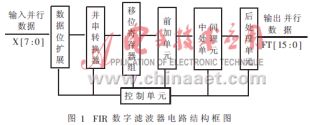
FIR低通数字滤波器电路分为数据位扩展、并串转换器、移位寄存器组、前加单元、中间处理单元、后处理单元以及控制单元等部分,其构成框图如图1所示。
2.2.1 数据位扩展
这里所设计的FIR数字滤波器输入是8位宽的,为了防止溢出,保证电路的正常工作,这里采用符号位扩展方法,经过符号位扩展,总的输入数据宽度为9位。
2.2.2 并/串转换器
并/串转换器由9个2选1选择器和9个D触发器组成,结构十分简单,在此不再对其电路结构赘述。其工作过程为:并/串转换器以采样速率周期地采入8位样点数据,并输出1位数据流给后级的移位寄存器。
2.2.3 移位寄存器组
寄存器组主要完成移位功能。
2.2.4 前加单元
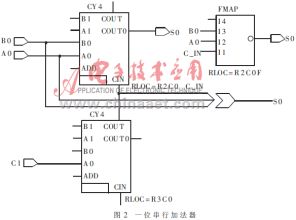
前加单元的主要功能是将移位寄存器输出的1位串行数据流进行预相加,它由一位串行加法器构成。XC4000系列芯片具有以下两个特点:
(1)内部基本单元CLB(可配置逻辑模块)包括三个函数发生器,分别以F、G和H标记。其中两个第一级的函数发生器F和G,每个可实现4输入的任何函数,同时它们也可以与H函数发生器组合生成五输入的任何函数。此外,CLB还具有CLB内部连线比外部连线延时小的特点。
(2)XC4000系列提供了快速进位逻辑(Carray Logic)用来加速加法器和计数器的进位通道。利用快速进位逻辑、加法器和计数器,在占用最小数量CLB的情况下,却具有极快的工作速度。且该进位逻辑可以进行灵活配置,以实现任意长度的计数器和减法器。
因此,从提高芯片利用率、布线率,减小电路延时等方面考虑,必须充分利用XC4000系列芯片的特点,对电路中的1位全加器作适合于FPGA特点的特殊设计。图2电路为本文所采用的经优化后的包括快速进位逻辑的1位全加器电路,其中FMAP为函数映射,可将特定电路映射到CLB的F、G或H函数发生器中;CY4为快速进位逻辑宏单元。
2.2.5 中间处理单元
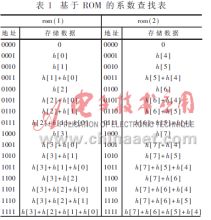
在FIR数字滤波器中,中间处理单元主要实现对来自前加单元的1位串行输出数据的相乘和累加功能。这里采用基于ROM查表法的分布式算法进行中间处理单元的电路设计。
如前所述,本文仅考虑冲激响应对称的情况,即滤波器的系数是对称的,所以独立系数的数目应等于1/2的阶数。对于16阶的FIR滤波器来说,其独立系数的个数为8个。这8个独立系数按表1所示的各种组合存储于2个基于ROM的查找表内。
2.2.6 后处理单元
后处理单元的主要功能是对数据进行四舍五入和从数据流中取出需要的数据。完成四舍五入功能需要一个16位的加法器,取数据则需要16位并行D触发器。
2.2.7 控制单元
控制单元主要由计数器和D触发器组成。它对电路的控制主要包括:在电路开始工作前进行全局复位,作好工作准备;对输入单元的工作进行控制;提供中间处理单元正常工作所必须的一些信号;提供最终输出结果时的输出同步信号(OUTSYN)。
2.3 电路原理及功能仿真
采用Xilinx公司的XC4005EPC84设计的16阶FIR低通数字滤波器的硬件电路最上层的电路原理图如图3所示。
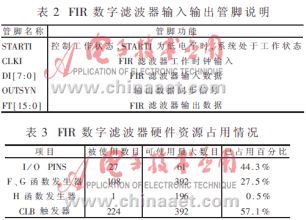
图3是FIR数字滤波器的上层图,其输入输出管脚情况和硬件资源占用情况分别见表2和表3。
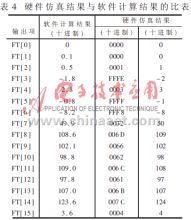
为了检测设计的电路能否连续正确地工作,连续输入了16位数据(十进制),分别为:100,101,102,103,104,105,106,107,-101,-102,-103,-104,-105,-106,-107。FIR数字滤波器硬件仿真结果(前16个输出)如表4所示。在表4中同时列出了根据文献[4]编写的程序所得到的软件计算结果。
从上述数据可以看出,软件仿真结果与硬件仿真结果相比,误差的绝对值均≤1,可以认为滤波器的硬件电路工作正确。
此外,为了验证此滤波器在边缘值输入时能否正确工作,还进行了边缘值测试。当输入数据是8位时,其两个边缘值分别是+127和-128,对应16进制的7F和80。利用这两组数据做输入,得到的输出也与软件结果进行对比,可以证实此时电路也能正确工作。
本文设计的16阶线性相位FIR数字低通滤波器,利用XC4005EPC84-2芯片实现时,处理数据的系统时钟频率为36MHz,采样速率为4MHz,计算结果和软件计算结果相比最大误差≤±1。在实际使用时,还可以根据不同精度要求,方便地对该FIR滤波器进行修改以满足不同的指标要求。另外,在本文设计的低通滤波器基础上,可以通过简单地重组滤波器特性参数,得到高通或带通滤波器。同时FPGA器件的可编程特性,可方便地对电路进行改进,便于电路性能的进一步提高。
参考文献
1 陈小元,王志华.用位串行算法实现抽取滤波器.电路与系统学报,1997;2(3):24-29
2 向 晖.二维DCT/IDCT处理器及FIR数字滤波器的研制.天津大学研究生毕业论文,1997.12
3 A. Peled and B. Liu.A New Hardware Realization of Digital Filters.IEEE Trans.on Acoust.& Signal process,1974(6):456~462
4 Samuel D.Stearns and David R. A.Signal Processing Algorithms.Prentice-Hall Inc.,1988