摘   要： 图像稀疏化技术是利用图像中稀少的且与具体应用相关的数据来表示原始图像的技术。使用BSP和遗传算法的方法在图像中生成能够近似图像的自适应的网格，即用较少的包含重要信息的像素来表示图像，实现图像的稀疏化，达到压缩之目的。该自适应网格能够以很高的质量重构出原始图像，在图像处理和计算机视觉领域有很好的应用前景。
关键词： 稀疏化；BSP；遗传算法；自适应网格

　图像的表示是寻求一种适合的方式来对图像进行更为方便的操作，就像把图像表示为离散的矩阵形式是为了方便计算机操作一样。图像的稀疏表示在图像处理[1]和计算机视觉[2]领域有着很好的应用，它能压缩图像，加快处理过程，更有利于具体应用领域的求解。用网格表示稀疏化的图像在该领域中有着重要的研究地位，通常先去掉图像中冗余的像素点，保留含有关键信息的像素，然后在这些像素点上生成网格来近似图像。本文提出的稀疏化的方法是将图像递归地划分为一个个满足要求的三角形，用三角形所构成的网格来表示图像。用遗传算法聚类来划分三角形，用BSP树结构来记录图像划分的结构，同时划分的三角形要求能够很好地表示其内部的像素，即能重构出其内部的像素，否则该三角形需要进行进一步地划分，因此三角形所形成的网格具有自适应性。
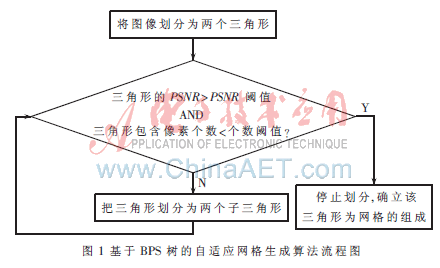
1 使用BSP树构建自适应网格
　给定一幅图像，构建一个图像的自适应网格来表示。从图像中选取少量的包含图像重要信息的像素作为网格的节点，为此选取BSP树来保存该划分的网格结构。二叉空间划分BPS[3](Binary Space Partition)是计算机图形学中常用的画家算法，在二维平面内，一根直线可以将该平面划分为两个半平面，在半平面内的直线还可以将该半平面划分为更小的子平面，这一过程可以一直进行。因此可以用BPS树来存储这一划分的平面。在本文中，将要处理的图像递归地划分为一个个三角形，所划分的三角形组成网格结构，每一次递归划分过程中要判断所划分的三角形是否满足预定的标准，满足标准则停止划分该三角形，不满足则继续划分。BPS树用来保存这一迭代的划分过程，其中非叶子节点保存用于划分的分割线，所有的叶子节点则保存划分后的三角形。
　首先，要确定三角形的划分标准。要求网格中的三角形能重构出其内部的所有像素点，具有自适应性，为此需要找到一个标准来量化原始图像的像素并利用网格中节点重构出图像的对应像素间的异度。本文选取峰值信噪比来衡量对应像素点间灰度的差异度。一幅灰度图像的峰值信噪比PSNR定义如下：

　其中，(xi,yi)是三角形3个顶点的坐标，(xn,yn)是三角形内部像素的坐标，因此利用式(4)可求出wi，再代入式(3)计算出In的值，便可计算出PSNR了。很明显重构出的图像越接近于原始图像，三角形的PSNR值越大。为了让网格高质量地重构出图像,一般设立一个较高的PSNR阈值，例如30 dB~40 dB。如果划分的三角形不满足此阈值则继续划分，直到满足条件为止。
　另外，选取三角形内所包含像素点的多少作为三角划分的另一终止的条件，以防止三角形过大、过稀疏化。当然可以根据生成稀疏图像的具体应用场景来设置该阈值。用BPS构建自适应网格的流程图如图1所示。

2 用遗传算法进行三角划分
　对于达不到阈值、不满足条件的三角形，要进一步进行划分。本文提出用遗传算法聚类[4]的方法来划分三角形。遗传算法是借鉴生物界进化规律演化而来的一种随机化的搜索算法，其主要特点是:直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐形并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向。
　本文利用遗传算法将三角形内部像素聚为两类，通过三角形顶点和两个类中心的中点的连线划分三角形。基因编码采用浮点数编码，用像素点的二维坐标表示。首先，建立n个种群(可调整n的值与三角形包含像素个数的多少成正比)，每个种群随机地选取三角形内的两个像素点c1、c2作为种群的个体，即初始的两个类中心。适应度函数定义为三角形内所有像素点到离它们最邻近的类中心的平均欧氏距离，定义如下：
    
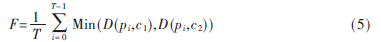
其中，c1和c2是种群的个体，pi是三角形内的像素点，D是欧式距离，T是三角形内像素的个数。很显然，F值越小适应度越高。
    要求计算出所有种群的适应度函数，然后采用轮盘赌选择算法选取m个种群进入下一代，适应度越高的种群进入下一代的概率越大。对剩下的n-m个种群进行交叉和变异操作。交叉操作是选取未进入下一代的某一种群中的一个类中心，与其他任意一个种群的类中心进行交换，保存交换后的两个个体，并将该种群放入下一代。变异操作是以小概率的事件发生选取未进入下一代的某一种群中的一个类中心，将其坐标值朝任意方向增长随机步长，保存其值，然后进入下一代。再重新计算出下一代的每个种群的适应度，此过程一直迭代，直到满足终止条件为止。本文以迭代次数作为遗传算法的终止条件，所有迭代进行完后，选取适应度最高的种群作为最优解，即找到了三角形内的两个类中心。

3 实验结果
　本实验对如图3所示的512×512的Lena灰度图像进行实验，使用基于BSP和遗传算法技术对原始图像稀疏化所生成的自适应的网格如图4所示。该网格由一个个三角形组成，删除了大量的冗余信息，同时保存了图像的重要信息。该稀疏图像在PSNR=30 dB的条件下生成，所生成三角形的数量约为3万个，相对于其他网格表示[5-6]技术，本文提出的方法在压缩率上有近30%的提高。用该网格重构出的近似图像(PSNR=30 dB) 如图5所示，从视觉直观判断，重构出的图像稍有平滑的效果，质量今人满意。

    本文提出了结合BSP和遗传算法的技术将图像稀疏化表示，用BSP树生成自适应的网格，用遗传算法分割网格中的三角形，同时该网格能以很高的质量重构出原始图像。所获得的稀疏化图像具有较高的压缩比，可应用在图像处理、计算机视觉等各个领域。
参考文献
[1] 徐大宏.基于正则化方法的图像复原算法研究[D].长沙：国防科技大学，2009.
[2] SARKIS M, DIEPOLD K. Sparse stereo matching using belief propagation[C].Image Processing. ICIP 2008.15th IEEE International Conference on. San Diego,CA.2008:1780-1783.
[3] SHIRLEY P.计算机图形学(第2版)[M].高春晓，译.北京:人民邮电出版社,2007.
[4] 傅景广，许刚，王裕国.基于遗传算法的聚类分析[J].计算机工程,2004,30(4):123-124
[5] YANG Y,WERNICK M N, BRANKOV J G. A fast approach for accurate content-adaptive mesh generation[J]. IEEE Transactions on Image Processing, 2003,12(8):866-880.
[6] RAMPONI G, CARRATO S. An adaptive sampling algorithm and its application on image coding[J]. Image and  Vision Computing,2001,19(7):451-460.