摘  要： 分析了耳蜗滤波器与小波变换" title="小波变换" target="_blank">小波变换的相似性，以耳蜗频率响应为基础，设计出相应的小波变换基函数，并通过二进尺度变换得到一组小波作为耳蜗滤波器组。研究了利用该小波滤波器组进行多分辨率分析的数字实现方法，给出了相应的分析滤波器。理论和实验结果均表明，利用小波变换来实现耳蜗滤波器组是可行的。 

    关键词： 耳蜗滤波器组; 离散小波变换; 多分辨分析; 语音信号处理

    耳蜗滤波器在语音增强、语音编码、语音识别等方面得到了广泛的应用^[1-2]。耳蜗滤波器的设计因此也成了语音信号处理研究的一个热点。耳蜗滤波器组的实现通常是在各频率点上分别设计滤波器，然后利用VLSI(Very Large Scale Integration)来实现。这种方法设计出的滤波器各通道相互独立，参数调整需要分别进行，增加了滤波器设计和修改的复杂度，并且由于采用模拟的方法，其可靠性和灵活性都受到了很大的限制^[3]。数字耳蜗的实现近年来得到了广泛的关注。Kate在1991年就提出了耳蜗滤波器数字实现的软件算法，Summerfield于1992年利用ASIC实现了该算法^[4]。然而这种数字滤波器是对耳蜗滤波器高度简化的模式，它只是由一个二阶滤波器后级联数个一阶滤波器构成。1997年，Lim^[5]设计出了基于VHDL的耳蜗滤波器组模型，不过他的滤波器是一阶Butterworth滤波器。随后也出现了一系列的数字滤波器模型, 然而这些滤波器都是对耳蜗滤波器组的高度简化，其频率响应与生物学的测试结果也相去较远。2002年,Apurva Mishra^[6]以耳蜗滤波器的Hubbard’s TWAmp模型的频率响应为基础，通过最小均方误差算法对模型的频率响应进行拟合，从而设计出数字滤波器的系数，他采用IIR的方式来实现，这种方法设计出的滤波器虽然与生物学模型吻合较好，但其普适性和设计的灵活性较差，而且IIR为非线性相位滤波器，相位失真会对听觉系统后续处理产生影响。 

    本研究将小波变换的多分辨时频分析思想引入到耳蜗滤波器组的设计中。利用生理学上获得的耳蜗频率响应数据设计小波基函数 (母小波)，通过母小波获得一组二进制离散小波基作为耳蜗滤波器组。这组滤波器覆盖了人类听觉范围，并且由于它们都源自母小波，所以具有很好的一致性，其频率响应与生理学结果也能很好地吻合。 

1 小波变换与耳蜗滤波器 

    耳蜗是内耳的主要组成部分，它是一条蜗牛状卷曲的管子，里面充满了液体，其形状示意如图1(a)所示。在耳蜗液体的中部有基膜，当有声波进入时，基膜的不同区域会对不同频率产生最大程度的响应，即沿基膜发生“谐振”。沿耳蜗各点的谐振频率分布如图1(a)所示。发生谐振时，基膜上的内毛细胞会将谐振信息转换为神经脉冲并通过听觉神经传输到大脑，也就是说，耳蜗的不同位置允许不同频率的声波信号通过^[7]。从这种响应模式的耳蜗的作用相当于沿基膜放置的一组带通滤波器。实验数据表明，这组滤波器的带宽成对数增大，其频率响应曲线呈现恒定Q值的特点，并且这些滤波器具有非对称的频率响应，在高频端比在低频端的下降更为陡峭。这种结构的滤波器组为听觉系统提供了一个多分辨率分析系统：当输入为快速变化持续时间短的信号时，其频率高，将会在高谐振频率的通道产生激励，而此通道滤波器带宽大，可以获得高的时间分辨率；而对频谱尖锐的信号则可提供很好的频率分辨率。所以，听觉系统的时频分析具有很高的灵活性和自适应性。 

    拉直后的耳蜗的频率响应特性如图1(b)所示，其中心频率随位置呈对数分布，将其频率响应记为H_ω(x-ln(ω))^[8]，ln(ω)表示自然底对数。 

    假设输入信号f(t)，其Fourier变换 

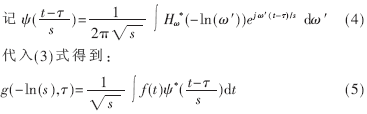
    这正是输入信号f(t)的连续小波变换。τ为平移参数，s为尺度参数。小波变换的基函数(母小波)： 

式中，WT_f(s,τ)表示f(t)的小波变换，其中的*表示卷积。取不同的尺度因子s，得到一组滤波器Ψ_s(τ),这组小波滤波器具有恒定的Q值，这与耳蜗滤波器组的恒Q特性也是相符的。 

    离散小波变换的小波基Ψ_n,m(t)是通过对小波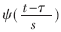的尺度参数和平移参数抽样得到的。实际中采用最多的是二进制抽样，a_m=2^-m，τ_n=na_m,得到离散化小波： 

    h_n,m(t)=2^m/2h(2^mt-n), m,n∈Z 

    这是一种自然的抽样，当比例因子以2为倍数增大时，小波滤波器的带宽以2为倍数减小，同时，平移的抽样率也以2为倍数减小，这样,一半的带宽采用一半的抽样率，可以有效避免数据冗余。二进制小波滤波器组的自适应性表现在：它利用一组恒Q值的带通滤波器将信号划分为若干倍频频带，并且在各频带内的时间抽样与带宽成正比。 

    上述分析表明，小波变换的特点与耳蜗的频率分析特性极为相似，小波变换引入耳蜗滤波器组的设计中。从耳蜗频率响应的实测数据中获得H_ω(x-ln(ω))，便可根据(6)式计算小波基，进而通过尺度变换得到一组带通滤波器，可以大大简化滤波器设计。传统的耳蜗滤波器组设计方法是对各通道分别设计，各通道相互独立，参数调整需要分别进行，增加了滤波器设计的复杂度。而基于小波变换的滤波器组设计就可以很好地回避这个问题。 

2 听觉小波滤波器组的设计与实现 

    人耳耳蜗响应的频率范围大约为20 Hz～20 kHz，其对数中心频率大约为f₀=1 kHz。参考文献[9]给出了这一中心频率的耳蜗滤波器的幅频响应曲线,如图2所示。

    利用MATLAB的invfreqz函数设计具有上述幅频特性的滤波器系数。这种方法设计出的滤波器的频率响应是给定频率响应在最小均方误差意义上的逼近。通过这组滤波器的系数便可得到相应的小波基函数Ψ(t)，如图3所示。 

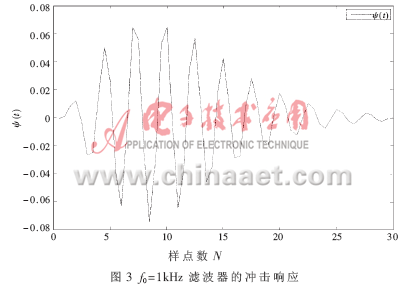
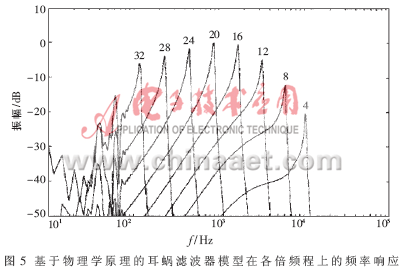
    以该冲击响应为小波基函数,通过二进制尺度变换得到一组小波，这组小波滤波器的中心频率从62.5 Hz(1 kHz×2^-4)到16 kHz(1 kHz×2⁴)呈对数分布,其幅频响应如图4所示。与基于物理学原理的耳蜗滤波器模型的频率响应相比较，可以看出，该小波滤波器组反映出了耳蜗滤波器的本质特征。图5是基于物理学原理的耳蜗滤波器模型在各倍频程上的频率响应。 

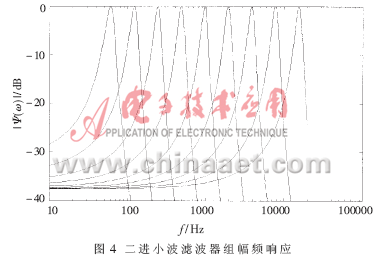
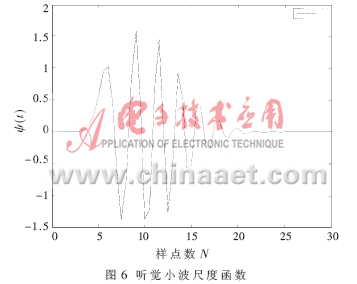
    得到小波函数Ψ(t)后，便可通过式(8)设计尺度函数φ(t)^[10]，得到的φ(t)如图6所示。 

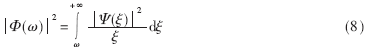
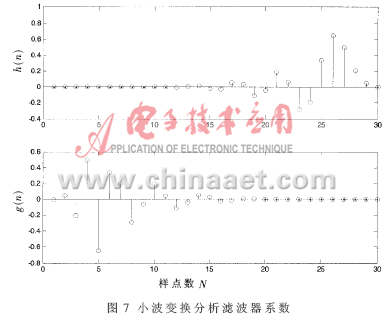
    结合Ψ(t)和φ(t)，通过关系式(9)、式(10)计算二进制小波用于多分辨率分析的低通滤波器H(ω)和高通滤波器G(ω),进而得到滤波器系数h(n)和g(n)^[11-12]，如图7所示。 

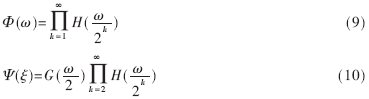
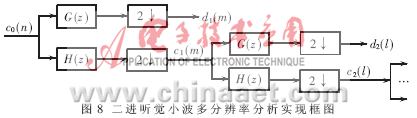
    二进听觉小波多分辨率分析实现框图如图8所示。 

3 实验结果及讨论 

    图9为用上述设计的听觉小波滤波器组对实际的语音信号进行处理的各通道的处理结果。其输入信号为男音，内容为“we，be”，采样率为10 kHz，8 bit量化。滤波器组的输出经过全波整流和低通滤波(截止频率300 Hz，二阶IIR滤波器)。 

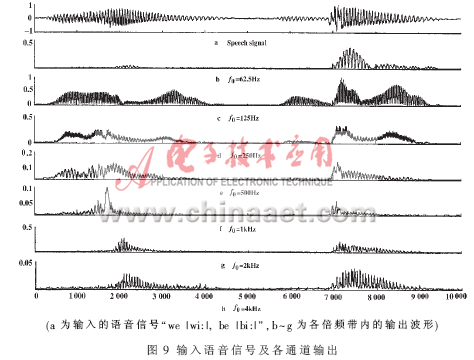
    图9中，a是输入语音信号的波形，b～g为各倍频带内的输出波形，由于语音信号频率一般在50 Hz～5 kHz以内，所以实验中只使用了62.5 Hz～4 kHz 这7个倍频通道。由实验结果可以看出，不同的音素会在不同的滤波通道出现，例如，半元音|w|(对应图中样点1～1 500)主要分布在中频段(f₀=125、250、500)三个通道；爆破音|b|滤(对应图中样点6 000～7 000)则基本只出现在f₀=125 Hz的通道，而元音|i:|则在低频段和高频段均会出现。可见，小波变换能很好地表征语音信号在频域内的特征。 

    二进听觉小波对信号实施逐级抽取(如图8)，使得抽样率自适应匹配信号带宽，从而有效减少了冗余数据。而且小波变换有快速算法，所以用小波变换来设计和实现耳蜗滤波器组可以提高语音处理系统的实时性。然而，从图9中也可以看出，这种方法的缺点就是它只能在各倍频程频率点上实现滤波，对频带的划分比较粗糙，而实际的生理系统中与耳蜗基膜相连的内毛细胞多达上万个，即耳蜗将听觉频段划分成了上万个子带进行处理。所以这种方法还有进一步的改进之处。 

    理论分析及实验结果均表明，二进制小波变换的特性与耳蜗滤波器组的特性存在很多相似之处，例如，频率的对数分布特性、滤波器组的恒Q特性等。利用小波变换来实现耳蜗滤波，不仅可以使滤波器的设计和修改大大简化，而且可以通过快速算法提高实时性。 

参考文献 

[1] YU Shao， CHANG Chip Hong. A generalized timefrequency subtraction method for robust speech enhancement based on wavelet filter banks modeling of human auditory system. IEEE Transactions on Systems,MAN, and Cybernetic, Part B: Cybernetics, 2007,37(4):877-889. 

[2] WONG Chun Kit. A decimated electronic cochlea on a reconfigurable platform, Master thesis, Chinese University of Hong Kong, July, 2006. 

[3] LEONG M P,JIN C T,LEONG P H W.An FPGAbased electronic cochlea. EURASIP Journal on Applied   Signal Processing, 2003(7):629-638. 

[4] SUMMERFIELD C D, LYON R F.ASIC implementation of the lyon cochlea model. Proc. IEEE Int.Conf.Acoust., Speech, and Signal Processing, San Francisco, CA, 1992:673-676. 

[5] LIM S C, TEMPLE A R, JONES S, et al. VHDLbased design of biologically inspired pitch detection system. in Proc. IEEE Int. Conf. Neural Networks, vol. 2, Houston, TX, 1997, pp. 922-927. 

[6] MISHRA A, HUBBARD A E. A cochlear filter implemented  with a field-programmable gate array. IEEE Transactions on Circuits and Systems II:Analog and Digital Signal Processing, 2002,49(1):54-60. 

[7] SALIMPOUR Y, ABOLHASSANI M D, ZADEH S H.Auditory wavelet transform. The 3rd European Medical and Biological Engineering Conference, November, 2005:20-25. 

[8] ALDROUBI A, UNCER M. Wavelets in medicine and biology. CRC press, Inc.1996:528-529. 

[9] KIANG N Y S. Processing of speech by the auditory nervous system. Acoust. Soc. Am,1980,68(3):830-835. 

[10] MALLAT S. A wavelet tour of signal processing.Academic Press, 1999. 

[11] KARMAKAR A, KUMAR A, PATNEY R K. Design of optimal wavelet packet trees based on auditory perception criterion. IEEE Signal Processing Letters,2007,14(4):240-243. 

[12] SALIMPOUR Y, ABOLHASSANI M D. Auditory wavelet transform based on auditory wavelet families. Proceedings of the 28th IEEE EMBS Annual International Conference New York City, USA, Aug 30-Sept 3, 2006.