一、前言

    硅微机械传感器是用半导体硅加工工艺实现的传感器。体积小使其获得广泛的应用前景。但是由于体积小，微小的绝对机械误差却产生较大的相对误差，带来运动交互干扰，即机械耦合问题。电容式硅微机械陀螺是用于测量转动角速度的传感器。由力学原理可知，由刚体转动（角速度ωe）和平动（线速度vr），可产生一正交的加速度（科利奥里加速度，科氏加速度ac）。

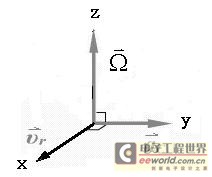
图1 科氏加速度
Fig. 1 Coriolis acceleration 
 
    在设计微陀螺结构时,为了提高灵敏度,往往使驱动轴和敏感轴的谐振频率尽量接近,从而增加了系统的机械耦合敏感性。由于制造工艺缺陷的存在,产生微结构质量不均匀、梁的弹性不平衡、阻尼不对称等制造误差。诸多因素致使驱动轴耦合到敏感轴的振动幅度加大,即机械耦合误差的增大,使结果产生一个偏移输出。这种耦合是制约微陀螺性能提高的关键问题之一。因此人们提出了各种结构的微陀螺抑制机械耦合。但是由于微陀螺本身的结构特点决定了机械耦合误差并不能被彻底消除。

    目前从电路方面着手，解决这个问题的方案是假定敏感方向位移与驱动方向位移正交，用相关检测的方法提取敏感信号。这也就是先假定无机械耦合的理想状态，然后通过电路相移微调，零位直流补偿缓解这一问题。

    对于微陀螺，以乘法器、低通滤波等模拟电路为核心相关检测器的任务是从大的背景干扰信号中高精度地分离出很小的科氏加速度敏感信息。通常背景干扰信号的幅度远大于敏感信号量程。由于模拟电路的非绝对线性，干扰信号和敏感信号都存在谐波与正负半波非对称等等问题，以乘法器、低通滤波为基础的相关检实际效果不佳，也不稳定。

    本文准备从文献中已经提出的机械耦合分析出发，提出一种敏感信号的读取方法：在耦合干扰过零点采样。

二、机械耦合分析

    我们以线振动微机械陀螺模型进行分析。对于理想化的（无机械耦合）微机械陀螺，在单测量自由度时，理论分析有

    驱动方向（x轴）位移 （1）
    敏感方向（y轴）位移      （2）

    其中 ωd 为驱动角速度；

    频率敏感系数；

    ω0s 为敏感方向固有振动角频率

    由于φ1 的存在，x(t)和y1(t)不完全正交，频率敏感系数随陀螺加工不一致性有关。如果假设敏感信号电压正比于敏感方向位移，在敏感电压输出中混有驱动电压干扰，暂不考虑电路相移，在相关检测器之前的信号输出为

        其中 A、B 为系数，B干扰系数；

    φud 驱动电压与驱动方向位移的相角差。

     实际上，B值比较大，即使在无机械耦合的理想条件下，有用敏感信号与电干扰也不完全正交。相关检测器参考电压的相位调整要首先保证去除电干扰。

    实际的机械耦合存在下列几个方面：

    1、质心G 偏离坐标原点,导致振动方向偏离驱动力方向,意味着驱动振动在敏感方向会产生一个分量。
    2、支承梁和梳齿的尺寸加工误差会产生刚度耦合、刚度不对称、驱动力不对称以及位移检测不对称等误差。
    3、由于气体阻尼和结构不对称产生阻尼耦合误差。

    对于线振动电容式硅微陀螺，在X方向的驱动电压会引起三种模态振动：驱动模态，振型为敏感质量沿X 方向的线振动；检测模态，振型为敏感质量沿Y 方向的线振动；旋转模态，振型为敏感质量绕Z 方向的角振动。对于理想化的（无机械耦合）硅微机械陀螺，仅驱动模态被激发，如果没有外界角速度输入，陀螺输出为零。受测量科氏力和机械耦合影响所产生的敏感加速度如图2所示。质心偏移和刚度耦合和驱动位移成正比，与驱动速度信号相位正交，因此刚度耦合误差将造成陀螺的正交耦合运动。阻尼耦合误差形成的干扰力与驱动速度成正比，该力与驱动速度信号和哥式加速度信号相位同相。由于硅微陀螺的Q值较高，特别是在真空硅微陀螺中，可以忽略阻尼干扰。一个简化的耦合模型如图3所示。

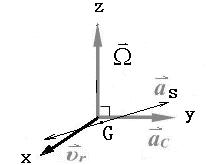
图 2 受测量科氏力和机械耦合影响所产生的敏感加速度 
 

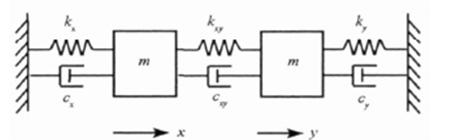
图3 　机械耦合影响下的微陀螺结构模型
Fig. 3 　Vibrating gyroscope model under mechanical coupling

    根据这个耦合模型得到一个近似稳态解

 
    其中 E2 为刚度耦合影响系数，与刚度耦合系数kxy ，y方向刚度ky有关；
E3 为阻尼耦合影响系数，与阻尼耦合系数Cxy ，y方向品质因数Qy有关。

    如果忽略真空硅陀螺中的同相阻尼影响，必然存在刚度耦合影响为零的时刻t0，使

 
     当φ1很小时，敏感位移峰值应出现在t0附近。在非线性较大的陀螺中，也可以利用Ω=0条件，搜索到绝对值y2最小点，作为零参考点。

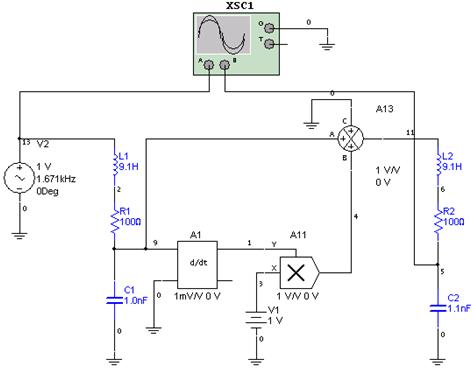
图 4 刚度耦合的电学模型
Fig. 4 Electric model under mechanical rigidity coupling

    图4为一维振动式硅微机械陀螺的电学仿真模型。L1、R1、C1分别代表驱动轴方向的质量、阻尼和刚度。L2、R2、C2分别代表敏感轴方向的质量、阻尼和刚度。V2等效为驱动力。

    C1、C2两端电压等效为驱动方向和敏感方向位移。V1代表转动角速度。A1对驱动方向位移的微分得到速度，A11乘法运算后得到科氏力。A13将刚度耦合与科氏力合成为敏感轴方向的驱动力。通过这个模型可以仿真不同条件下的敏感输出与驱动力V2的相位关系。也可以研究刚度耦合与敏感输出的相位关系。图4的近似仿真，主要是用于电路设计讨论。

三、采样方法设计

    根据以上分析，应该在机械耦合最小时采集敏感信号。由于正反向振动机械耦合可能不一致，机械耦合最小时刻应分别选取。利用振动时机械运动的惯性，在采样时关断驱动电压信号，消除电耦合干扰。

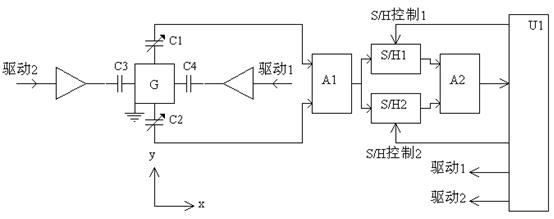
图 5 采集与驱动框图
G 微陀螺机械振动块；C1、C2 敏感电容； C3、C4 驱动电容；A1 差动电容调理电路；A2 差动放大器； S/H1、S/H2 采样保持器；U1 采集控制单片机
Fig. 5 sample and driver block
G vibration block of micromachined gyroscope;C1,C2 sensing capacitor; C3,C4 driving capacitor;A1 conditioner of differential capacitor; A2 differential amp.;S/H1,S/H2 simple-holder; U1 SCM
 
    图5为采集与驱动框图。控制时序由U1完成。为了精确控制时序，采用时钟频率较高的DSP器件，本实验采用的是TMS320F2810。控制时序如图6所示，采样时序脉冲发生在振动质量块过静态平衡点。实验过程：通过显微镜观察初步确定谐振频率范围；在零转速条件下，通过改变驱动频率寻找机械耦合最大的频率，并在有转速条件下，搜索信号输出最大的驱动频率，双方面验证找到机械谐振频率；在零转速条件下搜索到机械耦合最小的同步采样时刻。在这个时刻一般有转速时的敏感信号也接近最大值。初步试验结果：驱动周期3017Hz，转台转速0.1Hz，10次平均，数字输出信号跳动1%。

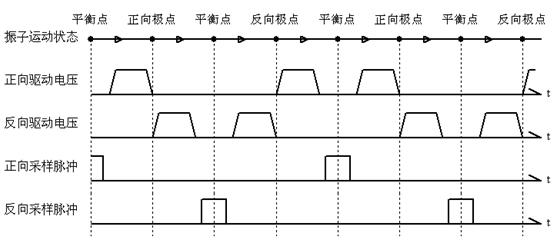
图 6 控制时序
Fig. 6 control order

    各脉冲可通过片上外设PWM接口送出，基本上不耗费软件时间。对于确定的硅微陀螺，一旦最初的搜索、标定完成后，脉冲时序便成为固定常数。正常运行时，软件仅完成简单的补偿修正工作。进一步还可以考虑用SOC器件，把S/H1、S/H2、A2、A/D、PWM、CPU等功能由一只芯片完成。

四、结束语

    任何硅微陀螺都不可避免地存在机械耦合干扰，本文分析指出存在干扰影响最小的可供对敏感信号采样时刻。这个采样时刻靠近敏感信号的峰值点。结合以前文章[]所提出的采样时关断驱动信号方法，可提高硅微陀螺的性能。笔者认为，由于各微陀螺仪谐振频率的差异，直接检测质量块过平衡点时刻的方法还需研究。这将是以后进一步的研究。