简化球体的BSP剖分结构的快速碰撞检测
2009-06-01
作者:于晓霞,沈志刚
摘 要:在动态场景中,碰撞检测遇到的最明显的问题就是需要对N个物体对进行两两求交测试,其时间复杂度达到O(N2)。提出了一种简化球体的BSP剖分结构的快速碰撞检测算法。首先用一种调度算法估计BSP树开始失衡的地方,再用一种策略来选择分割面,新结构在表示动态场景中不需要重新构建树,而是在保持树的平衡和合理的高度的同时通过自身的调节来达到更新。
关键词:碰撞检测;动态场景;BSP树
在动态场景的模拟中,当场景中物体的个数超过2个,碰撞检测遇到的最明显的问题就是需要对所有N个物体进行两两求交检测,其时间复杂度达到O(N2)。为此,加快这种检测速度通常是用两步算法[1]。所谓两步法,就是在第一步(也称初步检测阶段),首先将多数明显不相交的物体对进行快速排除,找出潜在的相交区域或潜在的相交物体对;然后在第二阶段根据已经确定的潜在的相交区域或潜在的相交物体对几何做进一步的相交测试,这一步也称详细检测阶段。在处理动态场景初步检测时,BSP树算法在快速排除明显不发生碰撞的物体不够理想,为此本文提出了一种基于BSP结构的快速碰撞检测算法。该算法是在BSP树结构的更新操作时,定义了5种操作算子,并通过一种调度策略执行算子,保持BSP树结构的平衡。
1 BSP树的构建
BSP树是最常用的空间剖分技术,Fuchs 于1980 年首次将BSP技术中剖分平面的定侧性质应用于多边形场景的剖分[2],BSP 树是一个用来对 n维空间内多面体进行排序和查找操作的标准的二叉树。这个树代表了整个场景,每一个叶节点代表着场景的1个凸集多边形集合,每一个非叶节点包含一个分割平面,这个分割平面将1个子场景分成2个更小的场景。BSP 树的构造是这样一个过程,已有一个子场景,用这个场景中1个多边形所在的平面从内部分割这个场景,结果又得到2个子场景然后继续循环分割它们,直到所有子场景都是一个凸集多边形集合为止。BSP树就是一个二叉树,叶节点存储场景多边形,非叶节点存储分割面。图1所示,为二维平面上的BSP树结构剖分。
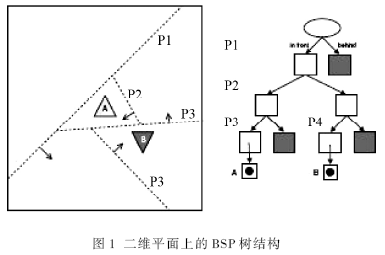
BSP在计算碰撞检测时有巨大的优势,它能够很容易定位运动物体在BSP树的具体位置,即场景中的具体位置。定位完成后,只有很少数目的多边形需要检测,即每一帧里只检测物体是否穿过那些组成它所在叶节点的多边形[3-4]。
2 简化球体BSP剖分结构的分割面选取策略
当创建一个 BSP 树时,决定是否需要一个平衡树,也就是说树的左右分支的深度的差异不应该太大,由于每一次分割都会产生新的多边形,因此应尽量减少分割的次数。如果在 BSP 树的创建过程中产生了太多的新多边形,显示卡就要花更多的时间来处理多边形的渲染,使一个不平衡的树将用更长的时间来进行树的遍历。因此在选择分割面时,应该根据下面的标准(p为分割面) :
population(p)由分割面所生成节点所包含物体的数目。
balance(p)被分割面分割成的左右子树深度的比率。
redundancy(p)横跨分割面的物体的数目。
即在选择分割面时,需要综合考虑以上3个条件,选择balance最大、redundancy最少的分割面。
分割面的选取方法一般采用直接选择平面法,是指从表示场景的多边形集合中随机选出一个多边形,假定该多边形在空间范围内无限延展,则平面将空间分成了2个子空间。在各自2个子空间内,原有的场景多边形分别位于其中,对于某一子空间,再从其中的多边形集合中任意选取1个,作为该子空间的超平面。这一过程递归进行,直到最终的子空间中只有唯一的景物为止。图2给出了这一过程的图形示意。
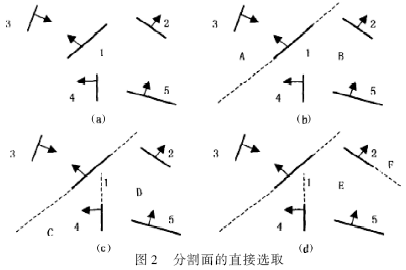
图2中,把各线段看作是垂直于纸面的平面,箭头为该平面的法向量,箭头所指方向为该平面的前面(可见一侧),其相反方向即为该平面的后面(不可见一侧)。图2(a)给出了初始的场景多边形集合以及每个多边形的法向量,在图2(b)中,首先选取面1为分割面,将空间分为A, B两个子空间;在B子空间中选取面4为分割面,将B分为C, D两个子空间;在D子空间中选取面2为分割面,将D分为E、F两个子空间。至此,整个空间划分完毕,每个子空间中只含有一个景物。
3 简化球体BSP剖分结构的更新操作
由于要保持动态物体在动态场景中的高效率的运动和一定的搜索特性,导致了BSP树结构的改变。如果重新构造树,额外的开销将严重影响碰撞检测的效率,因此,希望在原来树的基础上通过局部更新得到新的树。在这种情况下,更新树的过程时间开销就相当重要,如果更新树所花费的时间和完全重建差不多,更新就没有什么意义了。更新操作必须能够实时完成。本文采用的方法是根据动态物体的物理位置把它插入到BSP树的相应节点下,用BSP树逻辑操作修改BSP树的结构。下面将介绍是如何被调度来执行更新的。
3.1 分裂操作算子
当叶节点包含物体数量(population)大于给定的叶节点包含物体数量的阈值时,将该节点向下分裂,如图3所示。这样,一个新的分割面产生1个节点,同时生成两个左右子树。对于产生内部节点的分割面的选取按照上一部分提到的分割面的选择方法。对物体在候选分割面法线上的投影进行分类支配着这个操作的开销,为了减少这种开销只考虑这些物体1个子集。

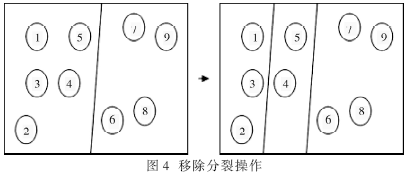
3.2 移除分裂操作算子
这个操作通过用存储在BSP树中的叶结点的信息来降低因分类而导致的使用分裂操作的开销。
在BSP树的构造过程中,每个叶节点将被整个放入表中。也就是从根节点(内节点)开始在节点上沿着它的父分割面的法线放置物体。在这张表中可以找出另一个法线方向与父分割面法线方向相平行的分割面。如果这个新的分割面满足分割面选择标准,就可以用移除分裂操作来代替分裂操作,如图4所示。
3.3 合并操作算子
合并操作算子的作用是:当一个叶节点连同它的兄弟所含物体数量之和还没超过阈值时,将它们向上合并。而且当由于物体的运动使分割面分割的区域出现空值时,它负责重新移动此分割面,(如图5)。
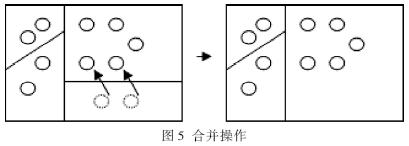
所有存储在合并节点的子树的叶节点的物体的有序表需要合并成一个。左右子树的节点自下而上合并,并且叶子节点代替原来的节点,如图6所示。每一个表需要沿着新的方向分类。当合并节点包含物体数量很少时,合并节点的子树通常也很小。

3.4 平衡操作算子
平衡操作算子的作用是:在原来树的基础上通过最小的改变来修复开始变得不平衡的节点。它适合于左右子树的深度差异很大的节点,即1个节点的1个子树所含物体数量很多而另一个子树几乎是空的。在这种情况下,利用平衡操作来取代合并子树操作,并通过移动分割面重新建立平衡,如图7所示。如果这个移动的分割面满足选择分割面的标准,可利用平衡操作来修改这个节点。

3.5 交换操作算子
交换操作算子的作用是:它适合于当平衡操作失败于重新建立平衡时的情况,在合并操作之前使用交换操作。交换操作删除不平衡的节点,用包含物体数量多的子树的根节点代替删除的不平衡节点结构的调整所需要的只是将包含物体数量少的子树插入,但这个操作很快,因为这个子树几乎是空的,如图8所示。

4 简化球体BSP剖分结构更新操作调度策略
BSP树结构的更新不同于物体位置的更新,因为树结构更新的时间开销很大,而且结构更新的好坏会导致碰撞检测对数目的增减,如果结构更新失败就会导致碰撞检测对数目的增加。定义的更新是在规定时间间隔内达到一个折中,即在更新的时间开销和树的高度之间。结构操作执行的时间顺序是至关重要的。更新BSP树结构的结构操作的调度策略说明如下:。
平衡操作是通过调整分割面来改善平衡,但是它会产生改变物体分布的副作用。这可能影响其他操作,在某些情况下可能变得不必要了。因此,在其他操作之前应该先考虑平衡操作,如图9所示。
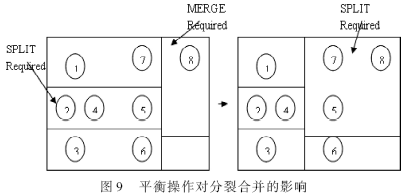
分裂操作是非常关键的,因为它是要把1个大的存放物体信息的顺序表分成2个小表,以降低更新顺序表的代价。首先是集中在所包含物体数量小于阈值的叶节点上,也就是通过对场景中的物体数量动态调整叶节点。而移动分裂操作是在分裂操作之前执行,也就是只有当移动分裂操作失效时才开始执行分裂操作。
当平衡操作失效时,交换操作开始执行。这个操作也如同平衡操作一样会产生副作用,通常导致小数量的物体移动。
合并操作是消除包含物体数量小于阈值的叶节点。这个操作不是很重要,因为对于小的顺序表的维持是很快的,而且额外的开销是保持几乎是空的节点和最小限度的叶节点。只有当在模拟的更新周期期间有自由的时间,这个操作才会被执行。
更新BSP树结构的结构操作调度策略如下:
开始遍历根节点为N的BSP树:
(1) If 节点N是不平衡节点;
(2) then评估平衡操作算子;
(3) If 平衡算子有效执行平衡操作;
(4) Else 调用交换算子;
(5) 停止遍历;
(6) End if ;
(7) 检查移动分裂操作,分裂操作,合并操作和调度时间表;
(8) if 所有事件已调度,停止遍历;
(9) Else 重复执行1~8步遍历节点N的每个子树;
(10) End if;
(11) 根据调度时间表估算被执行的事件数目;
(12) 执行移动分裂操作;
(13) 执行分裂操作;
(14) 执行交换分裂操作;
(15) 执行合并分裂操作。
5 实验结果与分析
为了验证BSP算法的性能,与QT quad(tree),Spatial Hash(SH)、LO loose(octrees),SP sweep-and-(prune)这4种算法进行了一系列比较实验。所有的实验都是在PIV2.5GHz、512MB内存的PC机上进行的。
每个模拟实验按每秒25步被评估4 min。实验评估包括执行效率(FPS),碰撞检测对的数目,初步碰撞检测阶段的时间,更新的时间(物体位置的更新时间和数据结构的更新时间)。
实验物体落入有限制的区域中,然后跟区域中的其他物体相互碰撞,这是利用了动态和静态物体之间的空间分割方法。因为静态物体对于提高执行速度是至关重要的。这种情景最适合BSP。BSP的碰撞检测时间最少,QT次之。SP的碰撞检测时间最坏但是更新时间跟BSP差不多。LO更新时间最佳。SH的更新时间最坏。
实验测试结果分别如 图10、图11、图12、图13所示。

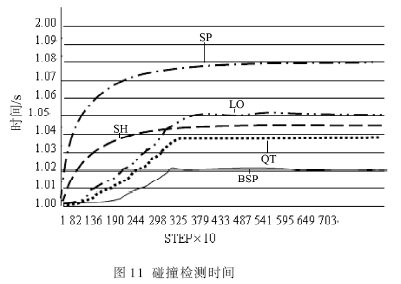
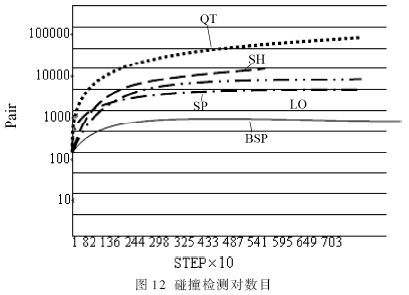

本文所介绍的方法主要目的是当碰撞检测对数目增加时,在计算碰撞检测对的代价和在空间数据结构中的结构更新代价两者之间建立一个折中的方法。实验结果表明,在初步碰撞检测阶段与SH、SP和LO方法相比,本文的方法是很有效的。虽然在碰撞检测对数目上与QT相似,但与QT相比,文中的方法对静态物体导致的空间分割模拟或者是高度集中的环境中产生太多碰撞的模拟是比较好的。文中各个更新BSP树结构的结构操作和调度策略的设计可以更好地重新利用存储在树中的信息来重新定位分裂面和稳定的执行效率。初步碰撞检测只是这种方法的一个应用,用这种方法来加快其他几何体的碰撞是今后要研究的另一个方面。
参考文献
[1] HUBBARD P M. 1995. Collision detection for interactive graphics applications. IEEE Transactions on Visualization and Computer Graphics, 1995, 1(3): 124-133.
[2] FUCHS H, KEDEM Z M,NAYLOR B F. H1 On visible surface generation by a priori tree structure [J]. Computer Graphics ,1980 , 14 (3) : 124-133.
[3] AR S, MONTAG G, TAL A. Deferred, self-organizing BSP trees. Computer Graphics Forum, 2002, 21(3): 269-278.
[4] JAMES D L, PAI D K. BD-Tree: Output-sensitive collision detection for reduced deformable models. ACM Transactions on Graphics (SIGGRAPH), 2004, 23(3).

