摘  要： SoPC是Altera公司近年来提出的一种灵活、高效的软硬件协同设计可编程片上系统。本文首先搭建硬件平台，在此平台上进行软件开发，运用改进免疫克隆选择算法解决函数优化问题。仿真结果表明，在SoPC上处理函数问题是可行的，并且算法具有优良的收敛速度及实时处理和抗退化能力。 

    关键词： 可编程片上系统；嵌入式系统；函数优化；免疫克隆选择算法

    实际工程中，有很多问题都可转化为函数优化问题，而基于梯度的算法通常不能有效地解决高维且有多局部极值点的函数优化问题。免疫系统是一种集进化机制和免疫机制于一体的全局并行系统，能自适应地维持群体多样性，其具有的自我调节能力，能使免疫算法具有整体、局部搜索能力强的特点。这类算法在函数优化、数据挖掘等方面得到有效应用。 

1 SoPC技术^[1] 

    嵌入式系统用于一些特定专用设备，通常这些设备的硬件资源(如处理器、存储器)非常有限，并且对成本很敏感，有时对实时响应要求高。随着消费家电的智能化，嵌入式系统更显重要，手机、电子字典、交换机、路由器等都属于典型的嵌入式系统。 

    片上系统SoC(System on a Chip)指在单片集成系统级多元化的大规模功能模块，从而构成一个能够处理各种信息的集成电路。这个系统通常由一个主控单元和一些功能模块构成，主控单元是一个处理器，在这个主控单元的周围，根据系统功能配置功能模块，完成信号的接收、预处理、转换及执行任务，并将硬件逻辑和智能算法集成在一起。 

    可编程片上系统SoPC(System on Programmable Chip)技术提供了另一种实现SoC的途径，即用大规模可编程器件的FPGA实现SoC的功能。 

2 SoPC软硬件开发 

    Quartus II软件是Altera公司的综合开发工具，通过使用此开发工具，设计者可以创建、组织和管理自己的设计^[2]。 

2.1 硬件开发 

    硬件开发环境是在Quartus II工程中添加NiosII系统、锁相环模块、引脚等元件编译完成的。NiosII系统由CPU、存储器接口、标准外围设备和用户自定义的外围设备等组件组成。如图1所示。SoPC Builder将这些组件组合起来，生成对这些组件实例化的单个系统模块，并自动生成必要的总线逻辑，以将这些组件链接起来。uart_usb用于接收实验板的数据，4个7段数码管用于显示运行的代数。 

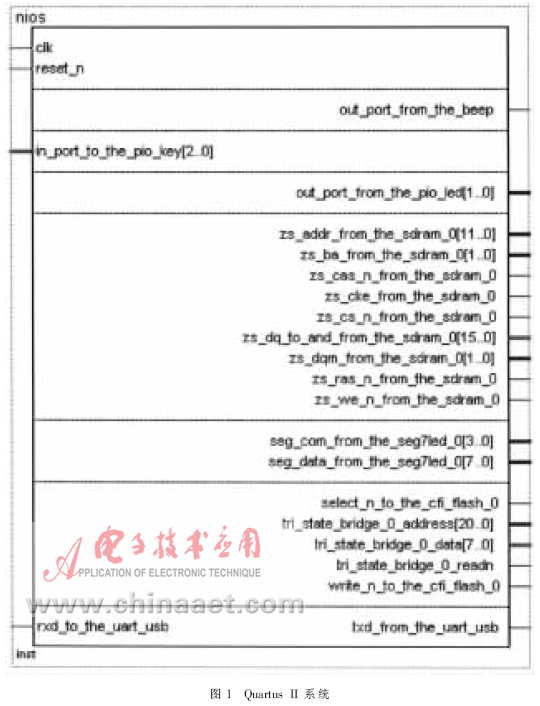
2.2 软件开发 

    软件设计和应用程序开发是在上述已搭建硬件环境上进行的，其开发环境是Nios II IDE。SoPC软件开发流程如图2。 

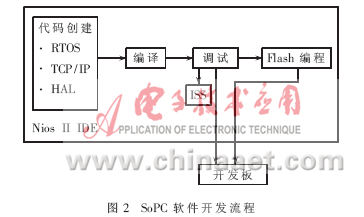
3 免疫算法原理 

    免疫算法的灵感来自生物获得性免疫克隆选择原理^[3]。根据该原理，在生物免疫系统中，一旦病原侵入机体，B淋巴细胞能够为产生相应的抗体和抗原的结合，同时活化、增殖和分化产生浆细胞，通过中和、溶解和调理等作用，最终使抗原从体内清除。一些B细胞成为长期存活的记忆细胞，它通过血液、淋巴和组织液循环，为下一次快速、高效地清除相同或者类似抗原引起的感染奠定了基础^[5]。 

    文本采用基于克隆选择原理的免疫优化算法^[4]。克隆选择学说的中心思想是：抗体是天然产物，以受体的形式存在于细胞表面，抗原可与之选择性地反应。抗原与相应抗体受体的反应可导致细胞克隆性增殖，该群体具有相同的抗体特异性，其中某些细胞克隆分化为抗体生成细胞，另一些形成免疫记忆细胞，以参加之后的二次免疫反应。 

    本文的算法是基于标准克隆选择算法改进而来的，标准克隆选择算法流程如图3。 

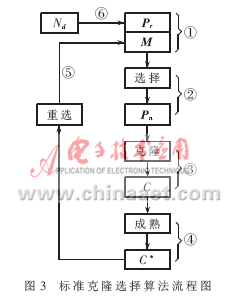
    (1)生成候选方案的一个集合(P)。它由记忆细胞(M)的子集加上剩余群体(P_r)(P=P_r+M)组成。 

    (2)选择n个具有较高亲和力的个体。 

    (3)克隆这n个最好的个体，组成一个临时的克隆群体(C)。与抗原亲和力越高，个体在克隆时规模也就越大。 

    (4)把克隆躯体提交到高频变异，根据亲和力的大小决定变异，产生一个成熟的抗体种群C^*。 

    (5)对C^*进行重新选择，组成记忆细胞集合M。P中的一些成员可以被C^*的其他一些改进的成员替换掉。 

    (6)生成d个新的抗体取代P中d个低亲和力的抗体，保持多样性。 

    本文提出一种改进克隆选择算法，用于求解函数优化问题。本文采用二进制编码，将该函数的值空间映射到位串空间中，然后在位串空间进行免疫克隆选择操作，结果通过解码过程还原成数值解，再进行亲和力评估。由于对函数的精度要求是6位小数，（1/2²²≈2×10^-6），所以本文的编码长度为6位。改进后的算法的实现步骤如下： 

    (1)初始化：随机产生N个长度为22的二进制编码的抗体，组成初始抗体P。 

    (2)克隆：对抗体群P中的抗体进行扩增操作得到群体C，每个抗体的克隆数目与亲和力(函数值)成正比。 

    (3)高频变异：对抗体群C中的抗体进行高频变异得到种群C^*。 

    (4)选择：从抗体群中选择d个亲和力高的抗体替换P中的d个亲和力低的抗体，d与抗体群P的平均亲和力成反比。 

    (5)判断终止条件，否则转(2)。 

    (6)达到终止条件，程序结束。 

4 仿真实验 

    本文算法的参数设置^[6]如下：受体编辑系数P_c=0.2；高频变异概率P_m=0.01；种群规模P_opsize=50；算法迭50代结束。仿真选取f=x+10×sin(5x)+7×cos(4x)，x∈[0，10]：一个单变量、多极值点的函数，用来测试优化算法是否能搜索到函数的最优解。 

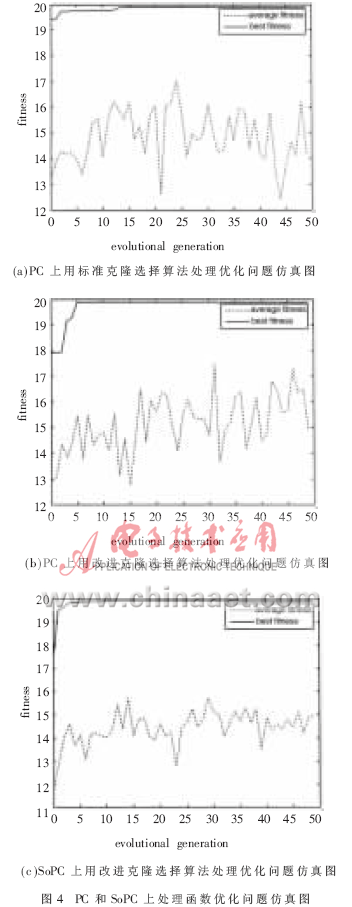
    在PC上分别运用标准和改进后的克隆选择算法处理函数优化问题，从图4(a)、图4(b)不难看出，改进后算法在第6代就能迅速达到全局最优，而标准算法需要13代。改进后算法在处理函数优化问题时提高了收敛速度。 

    运用改进的克隆选择算法处理函数优化问题，从图4(b)、图4(c)不难看出，在SoPC上运行了4代就得到了全局最优而每一代处理时间约0.35 s，达到最优所需时间约为1.4 s。而在PC机上运行6代后得到的最优结果，其每一代处理时间约为0.27 s，运行6代所需时间约为1.62 s。 

    不管在SoPC还是PC上，免疫克隆算法处理函数优化问题在进入局部最小的时候，总能跳出这个局部最小，从而达到另一最小，进而达到全局最小。这体现了算法的抗退化能力。 

    本文将改进免疫克隆选择算法应用在SoPC上，在实验开发板上搭建了硬件平台，在此基础上进行软件开发。实验表明，在PC机和SoPC上都能有效求解函数优化问题和避免陷入局部最小并达到全局最优。当资源明显不如PC机的情况下，在SoPC上处理到第4代就能迅速达到全局最优，而在PC机上则需要6代。获得这样的结果足以表明，SoPC有较强的优化和实时处理问题的能力。 

参考文献 

[1] 杨春玲，张辉.现代可编程逻辑器件及SoPC应用技术[M].哈尔滨：哈尔滨工业大学出版社，2005. 

[2] 汪国强.SoPC技术与应用.北京：机械工业出版社，2006. 

[3] DASGUPTA D.Artificial immune systems and their applications[M].Springer，1998. 

[4] BURNET F M.The clone selection theory of acquired immunity.Cambridge University Press，1959. 

[5] 莫宏伟.人工免疫系统原理与应用[M].哈尔滨：哈尔滨工业大学出版社，2002. 

[6] 焦李成.免疫优化计算、学习与应用与识别[M].北京：科学出版社，2006.