基于FPGA的改进型FIR滤波器的实现
2009-07-02
作者:黄晓红,蔡江利
摘 要: 利用分布式算法对FIR滤波器的硬件实现进行了探讨,在数乘累加的理论上,对分布式算法的串行、并行和拆分查找表法的FPGA硬件实现方法进行了研究。结合FPGA查找表结构,兼顾资源及运行速度的要求,用拆分查找表的方法设计了16阶8位常系数FIR滤波器,并在Quartus II 5.0下进行仿真,仿真结果验证了该算法的有效性和实时性。
关键词: FPGA;分布式算法;拆分查找表;FIR滤波器
FIR数字滤波器在数字信号处理的过程中有很好的线性相位和稳定性,被广泛应用于音频处理、语音处理、信息系统等各种系统中。随着现代电子技术及EDA技术的发展,特别是可编程逻辑电路的发展,FIR数字滤波器的实现将变得更具有灵活性和实时性。FIR滤波器的实现有多种方法,其中基于分布式算法FIR滤波器的FPGA实现采用硬件结构,此算法的特点是运行速度快,能较好地实现实时处理,特别适合于高速实时的信号处理。本文提出了一种基于分布式算法改进型FIR滤波器的FPGA实现,并设计和实现了改进型FIR滤波器。
1 FIR数字滤波器的直接型结构
FIR数字滤波器的输入与输出可以用下式表示:
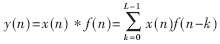
式中:N为滤波器的阶数(或抽头数);x(k)为第k时刻的输入样本值;h(k)为第k级抽头系数。FIR因为其单位脉冲响应h(n)是有限长而得名,即h(n)是一个有限长序列,对h(n)做Z变换就得到FIR数字滤波器的系统函数H(z):
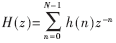
由此可以得到FIR数字滤波器直接型的结构图如图1所示。
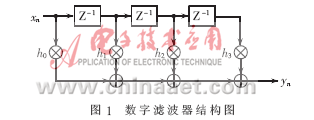
2 改进型FIR数字滤波器算法
2.1 分布式算法的原理
分布式算法是一种重要的FPGA技术,广泛应用在计算乘积和之中。除了卷积之外,相关、DFT计算和RNS反演映射等都可以转化为乘积和(sum of products)的形式。
(1)无符号分布式算法
假设N项的乘积和表示为:
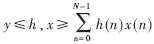
又设系数h(n)是已知的常系数,x(n)是变量,设x(n)的表达式如下:
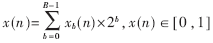
其中xb(n)表示x(n)的第b位,x(n)是x的第n次采样,则y又可以表示为:
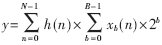
(2)有符号分布式算法
对于有符号数补码数采用补码的表示方法。需要注意的是,在补码中,最高有效位是用来区别正数和负数的。将采用(B+1)位表达式:
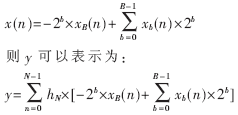
要实现有符号分布式系统,通常采用“带有加/减控制器的累加器”实现此系统,当xb(n)为0时进行加法运算,为1时进行减法运算。
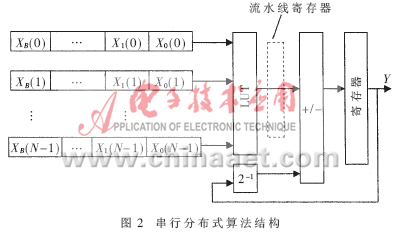
2.2 串行分布式算法
串行分布式算法结构如图2所示。利用一个LUT实现映射,即2N字宽,预先编写好程序的xb=[xb(0),xb(1),…,xb(N-1)]的映射,经查找表查找后输出,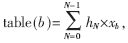 N次查询循环后就完成了计算结果。
N次查询循环后就完成了计算结果。
以三阶四位有符号的数字滤波器为例,令滤波器的系数为{-2,1,3},LUT可采用基于FPGA的逻辑查找表或利用FPGA自带的ROM实现。用case表实现的核心代码如下:
Process (table_ in)
Begin
Case table_ in is
when “000”=> table_ out<=0;
when “001”=> table_ out<=-2;
when “010”=> table_ out<=3;
when “011”=> table_ out<=1;
when “100”=> table_ out<=1;
when “101”=> table_ out<=-1;
when “110”=> table_ out<=4;
when “111”=> table_ out<=2;
when others=> table_ out<=0;
end case;
end process;
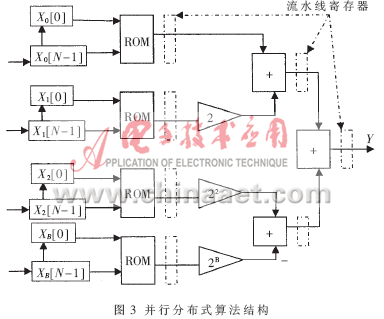
2.3 并行分布式算法
并行分布式算法结构如图3所示,图中虚线代表流水线寄存器,输入采用逐次采样(每次一个字)、位并行的形式。将每个数据的相同位递给LUT,对于输入的每一位都需要配置相应单独的表,且表的规模不固定(输入位宽等于滤波器抽头的数量),但表的内容相同。且不同的位对应不同的值,然后将从LUT中读取的数据经过处理后送入加法器中,每级的加法运算都是并行的。
2.4 拆分查找表
并行分布式算法虽然能够有效提高系统运算的速度,但是占用的资源太大。串行分布式算法占用的资源小,但系统的运算速度慢。而且当N很大时,即在FIR滤波器中如果阶数很高时,作为查找表的ROM将很大,例如:假定N=16,输入LUT的位宽为16,则ROM的大小为16×216 bit,即1 Gbit。N每增加一位,ROM容量就增加一倍,这种以2的幂次递增的资源占用是硬件资源不可接受的。
当系统对速度要求不太高、而滤波器的阶数很高时,可以采用拆分表减少ROM容量并将结果累加。如果再加上流水线寄存器,这个改进并没有降低速度,却可以极大减少LUT的设计规模。
假设长度为LN的内积:
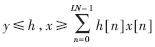
可以用一个DA结构实现。将和分配到L个独立的N阶并行DA的LUT之中,结果如下:
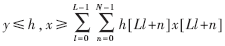
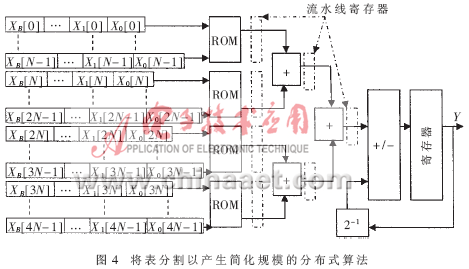
例如:实现一个4N的DA设计需要3个次辅助加法器。而表格的规模从一个4N×2B的LUT降低到4个N×2B表。图4是拆分查找表的硬件结构图。
3 基于FPGA实现的改进型FIR滤波器结构性能
3.1 16阶8位FIR滤波器的实现及仿真
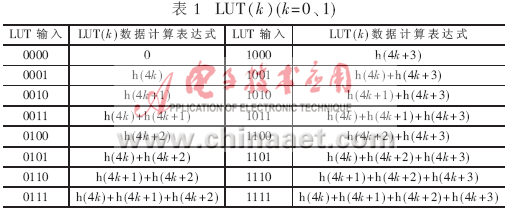
本设计采用Altera公司的Cyclone II EP2C35F672C8器件,在Quartus II 5.0下仿真,FIR滤波器为16阶,输入数据为8位(最高位代表符号位)。如果采用单个查找表的面积为28×16 bit,面积太大。采用拆分查找表的结构能减少面积,在Altera公司的一系列FPGA中LUT查找表采用四输入查找表,因此单个表可以拆分为2个四输入的查找表。因为设计的是线性相位滤波器,这样单个表的面积就得到了最优化。同时单个查找表的连线是LUT查找表的内部连线,减少了互联的资源和连线的延迟。查找表计算方法如表1所示。
设输入序列为{99,0,0,0,70,0,0,0,99,0,0,0,70,0,0,0},滤波器的系数为{-12 -18 13 29 -13 -52 14 162 242 14 -52 -13 29 13 -18}。仿真结果如图5所示。

本设计的时钟主频可达73.49 MHz,占用了236个逻辑单元,占整个LC(Logic cell)的2%。可见拆分查找表的方式实现FIR滤波器速度较快,占用的资源少。
若要实现更高阶的滤波器,拆分查找表法的优势将更加明显。另外,如果是线性相位的滤波器,表的个数将能缩小一倍。本设计即为线性相位滤波器。
3.2 改进型FIR滤波器在FPGA中实现的特点分析
为了分析改进型FIR滤波器在FPGA中实现的特点,利用VHDL语言程序分别设计了16阶的串行、并行及直接型FIR滤波器,并与相应的拆分查找表法FIR滤波器进行比较,其各自的运行速度及占用FPGA资源的情况如表2所示。
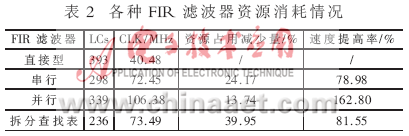
从表2可以看出,改进型滤波器与直接型相比存在两大明显的优势。一方面,在滤波器阶数相同时,改进型FIR滤波器在FPGA资源占用上比直接型更少;另一方面,系统运行的速度比直接型更快。而且,随着滤波器阶数的增加,这种优势更加明显。串行滤波器完成一次运算需要8个时钟周期,为了把数据分为8个时钟周期进行计算,采用了移位寄存器,这样单个表的面积相当大,从而占用了大量资源,工作速度也受到了限制。并行分布式滤波器在1个时钟周期完成了累加,提高了工作速度,但所用面积较大。拆分查找表法滤波器大大减少了面积,而且速度并没有降低。
本设计采用了拆分查找表方法,影响系统速度的是加法器组,可以对滤波器进一步改进,如对加法器组利用流水线、编码等技术可以提高工作速度。
通过以上的理论分析和仿真结果表明,基于FPGA器件的拆分查找表FIR算法,占用资源少、运算速度快,在资源允许的条件下可根据实际应用任意确定滤波器的长度和阶数,是一种比较实用可靠的高效设计方法。
参考文献
[1] PARHI K K.VLSI digital signal processing systems:Design and implementation[S].John Wiley&Sons,1999.
[2] ASHENDEN P J.The designer′s guide to VHDL(SecondEdition)[S].Elsevier Science(USA),2002.
[3] 程偑清.数字信号处理教程[M].北京:清华大学出版社,2001.

