基于非负矩阵分解的鲁棒哈希函数验证性研究-AET-电子技术应用

基于非负矩阵分解的鲁棒哈希函数验证性研究

来源：电子技术应用2012年第1期

吴荣玉, 樊丰, 舒建

电子科技大学电子工程学院, 四川成都611731

摘要： 矩阵分解是实现大规模数据处理与分析的一种有效工具。矩阵的非负矩阵分解NMF(Non-Negative Matrix Factorization)变换是一种正交变换，是在矩阵中所有元素均为非负的条件下对其实现的非负分解。鲁棒哈希技术利用密钥提取多媒体内容的某些鲁棒特征，通过进一步压缩产生哈希值，通过比较跟随媒体内容传送来的哈希和接收端产生的哈希，实现对媒体内容的真实性认证。

关键词： 非负矩阵分解哈希算法鲁棒性

中图分类号： TP391
文献标识码： A
文章编号： 0258-7998(2012)01-0130-03

Confirmatory study of the robust Hash function based on the decomposition of non-negative matrices

Wu Rongyu， Fan Feng， Shu Jian

School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

Abstract： Matrix factorization is an effective tool to realize mass data processing and analysis. Non-negative matrix factorization is a kind of orthogonal transformation. It can realize non-negative decomposition in the condition that all elements are non-negative. The technology of robust Hash use the secret key to extract some robust features from multimedia content, then,these features are compressed to produce hash value. We can authenticate the authenticity of media content through comparing the Hash transited along with the media content with the Hash produced by receiver.

Key words : non-negative matrix； Hash algorithm； robustness

随着网络通信技术的迅速发展和多媒体数字产品的爆炸式增长，大量的数字图像应用在日常生活和工作中。数字图像满足了人们的感观需要，也为人们的生活工作提供了便利。由于图像本身就是一个矩阵，所以矩阵的应用在数字图像处理中就显得尤为重要。

1 鲁棒Hash技术概述
鲁棒哈希是一种基于多媒体内容的数字摘要。现有的感知哈希认证方案主要结构如图1所示。

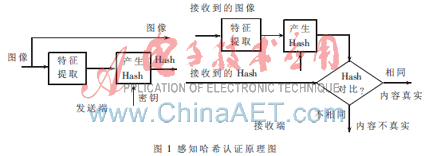
    在感知哈希的构造中，首先利用密钥提取多媒体内容的某些鲁棒特征，然后通过进一步的压缩产生哈希值。生成的哈希值被嵌入媒体或伴随着媒体传输到接收端，接收端的认证者使用与发送端相同的密钥对接收到的图像提取哈希。认证者通过比较跟随媒体内容传送来的哈希和接收端产生的哈希，就可以实现对媒体内容的真实性认证。
    对于图像哈希函数，有如下几方面要求：
   (1) 复杂度：哈希函数的算法应具有较低的计算复杂度。
   (2) 鲁棒性：相同感知的图像具有相同或相近的哈希值。传统哈希算法（MD5，SHA-1）对信息变动非常敏感，一个bit的信息变化都会造成生成的哈希序列完全不同。数字图像等多媒体数据可能会经过压缩增强等操作，这些操作虽然改变了图像信息，但并未影响图像的视觉内容。因此图像哈希算法需要考虑图像视觉域的内容信息改变，即相同内容的图像经过哈希函数运算生成的哈希序列应该相同或相近。
   (3) 唯一性：不同感知的图像经过哈希函数处理产生不同的哈希值。
　(4) 安全性：不同的密钥加密后，即使是相同的图像也要产生不同的哈希值。

3 NMF的鲁棒性实验及结果分析
    实验使用了15幅512×512的标准灰度测试图像baboon、boat、bridge、couple、crowd、girl、goldhill、lake、Lax、Lena、man、milkdrop、peppers、plane、woman2进行测试，如图2所示。

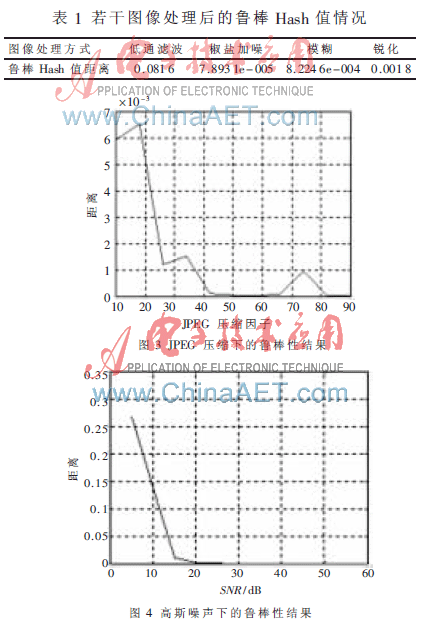
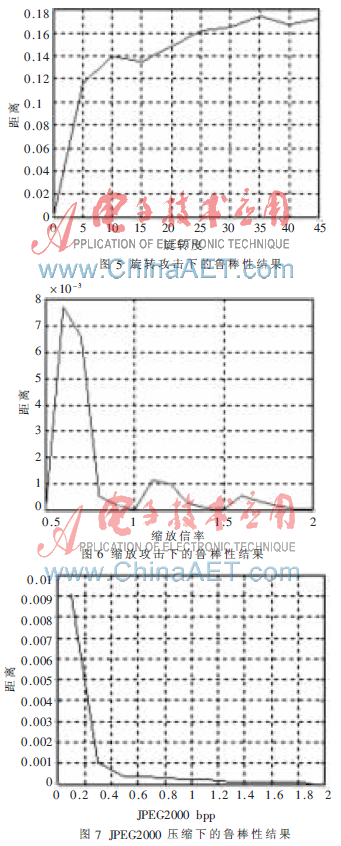
分别进行格式转换、滤波、剪切、比例缩放、JPEG压缩、叠加噪声、旋转后图像与原图像的哈希序列匹配测试，然后测试15幅图像Hash变换的平均值，实验结果如图3~图8所示。

图9~图12给出了一般的图像处理后的Lena图像的结果。表1给出了这四种图像处理后的鲁棒Hash值的变换情况。

根据实验结果图3~图12以及表1可以看出，NMF的Hash算法在抵抗图像压缩、加噪和缩放攻击时具有较好的鲁棒性，其Hash值的距离均不超过门限 0.03，而对其他一些信号处理如旋转、低通滤波、锐化和剪切类的几何攻击，鲁棒性比较差，即使一般的图像增强处理也无法保证足够的鲁棒性。

鲁棒Hash技术利用密钥提取多媒体内容的某些鲁棒特征，然后通过进一步的压缩产生哈希值。生成的哈希值被嵌入媒体或伴随着媒体传输到接收端，接收端的认证者使用与发送端相同的密钥对接收到的图像提取哈希。本文通过比较跟随媒体内容传送来的哈希和接收端产生的哈希，就可以实现对媒体内容的真实性认证。
本文针对非负矩阵分解鲁棒Hash技术进行了验证性的研究，设计了基于NMF的鲁棒Hash算法，并进行了大量的实验分析，通过分析发现，NMF有两个非常可取的方面：(1)由非负性限制带拉点可加性,使得用于捕捉图像的局部特征的“基”能显著的降低误分类概率；(2)图像空间域的几何攻击可以当作是NMF矢量中的独立同分布噪声。NMF的Hash算法在抵抗图像压缩、加噪和缩放攻击时具有较好的鲁棒性，其Hash值的距离均不超过门限0.03，而对其他一些信号处理如旋转、低通滤波、锐化和剪切类的几何攻击鲁棒性比较差，即使一般的图像增强处理也无法保证足够的鲁棒性。
参考文献
[1] Wang Shuozhong, Zhang Xinpeng. Recent development of perceptual image hashing[J]. Journal of Shanghai University, 2007,11(4),323-331.
[2] MONGA V, MIHCAK M K. Robust image hashing via non-negative matrix factorizations[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, 2006: II-225-228.
[3] SCHNEIDER M,CHANG S F. A robust content based digital signature for image authentication[C]. in Proc. IEEE Int. Conf. Image Processing, Lausanne, Switzerland, 1996.
[4] KAILASANATHAN C, NAINI R C. Image authentication surviving acceptable modifications using statistical measures and K-Mean Segmentation[C]. IEEE-EURASIP Work. Nonlinear Sig. and Image Proc., 2001.
[5] ALGHONIEMY M, TEWFIK A H. Geometric invariance in image watermarking[J]. IEEE Trans. Image Process, 2004,13(2):145-153.
[6] 叶卫国，韩水华.基于内容的图像Hash算法及其性能评估[J].东南大学学报(自然科学版)，2007(s1):109－113.
[7] 张维克,孔祥维，尤新刚.安全鲁棒的图像感知哈希技术[J].东南大学学报(自然科学版)，2007(s1):188－192.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容