由电压型逆变器和感应电动机组成的交流变频调速系统在空载或轻载条件下运行时，一些频段上（例如20 Hz～30 Hz）很容易发生自激振荡现象。这种现象不仅会引起错误的机械振动，而且会使电机电流大幅振荡，转速波动严重，缩短了电机和其他电气设备的使用寿命，大大影响了系统的控制精度和可靠性。随着交流传动技术的不断完善，为进一步提高系统性能，如何解决自激振荡问题成为人们研究的目标之一。

    随着电力电子技术的发展，人们对交流调速系统的性能要求越来越高。近些年来，国内外学者对感应电机自激振荡进行了研究[1-10]，并取得了一些研究成果。
    本文对基于转矩电流分量的调节频率指令法、基于合成电流的调节频率指令法、基于合成电流的调节电压指令法三种振荡抑制策略进行了研究，并对三种方法的实验结果进行了比较。
1 自激振荡抑制策略研究
    电机的振荡情况可以通过相电流的波动情况反映出来，而且对于变频调速系统而言，相电流的检测也是必不可少的。可以通过检测相电流得到准确可靠的振荡判据，并采取措施抑制振荡。该方法不需要增加硬件成本，实现简单，成为目前主要的研究热点。本文研究的三种方法均以检测相电流为基础。
1.1 基于转矩电流分量的调节频率指令法
    逆变器输入到电机的功率包含无功功率和有功功率，而无功功率大部分用来产生旋转磁场，有功功率大部分产生电磁转矩。设逆变器输入到电机的三相电流为iu、iv、iw，通过坐标变换将三相电流变换到以定子电压矢量为d轴的同步旋转坐标上，从而实现有功电流id和无功电流iq的解耦：



    通过以上分析可以看出，该方案不增加硬件成本，不受电机参数、逆变器参数等影响。由于有功电流分量是根据三相定子电流实时计算出来的，因此对稳定性影响最大的是三相电流的检测和滤波处理。如果检测有误差、时延或瞬态波动，则会引起调节频率的较大波动，从而可能引入新的不稳定因素。
1.2 基于合成电流的调节频率指令法
    基于转矩电流分量的调节频率指令法以旋转坐标系中的转矩电流分量的变化率作为不稳定度，对于以SVPWM调制方式的系统而言，实现该方法比较容易。但是对于原来不是基于旋转磁场控制的系统而言，实现起来较为困难。基于对振荡发生时定子电流变化的认识，本节讨论如何以定子电流的变化率作为不稳定度，设计PI调节器输出频率调节量，从而达到抑制振荡的目的。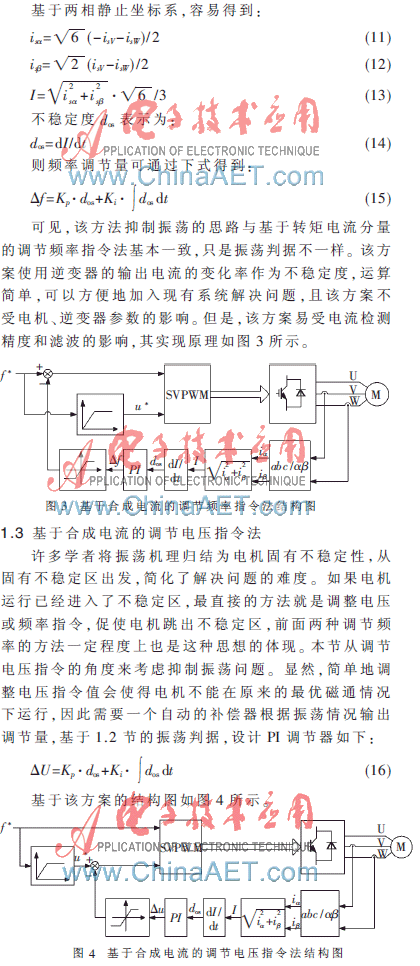

2 实验验证及对比分析
    在以TMS320LF2407A DSP为内核的7.5 kW实验平台上对基于转矩电流分量的调节频率指令法、基于合成电流的调节频率指令法、基于合成电流的调节电压指令法三种振荡抑制策略进行了研究，并对三种方案的实验结果进行了对比。
2.1 基于转矩电流分量的调节频率指令法
    图5为采用基于转矩电流分量的调节频率指令法，振荡抑制前后相电流和转速实验波形图。比较抑制前后的波形图可以看出，电流和转速的振荡得到很大的抑制。抑制前，电流畸变较大，幅值跳变严重，周期不明确，转速振荡严重，变化剧烈；振荡抑制算法启动后，电流波形畸变明显变小，正弦度较好，周期明确，转速波动也明显减小。

2.3 基于合成电流的调节电压指令法
    图7为采用基于合成电流的调节电压指令法振荡抑制前后相电流和转速实验波形图。可以看出，虽然抑制后电流仍有轻微波动，但是从整体来看，该方案抑制振荡效果是明显的。

    可以看出三种方案抑制振荡效果都比较显著。综合比较三种方案，在适用性方面，三种方案均不受逆变器、电机参数影响，适用性较好；从实验效果上看，方案1效果最好，抑制后电流正弦度最好，但如果考虑实际应用中的复杂工况，由于方案3的调节量是PI作用的输出，不会造成被调节量的突变，更适合于工程实用。本文通过实验得出：频率调节量控制在0.5 Hz～1 Hz为宜，电压调节量以不超过额定电压5%为宜。
    本文对基于转矩电流分量的调节频率指令法、基于合成电流的调节频率指令法、基于合成电流的调节电压指令法三种振荡抑制策略进行了研究，并对三种方法进行了实验验证，结果表明三种方案抑制振荡效果良好，并且不受电机、逆变器参数影响，可以方便地加入现有调速系统中实现振荡抑制。
参考文献
[1] Hu Chenfeng，Hong Rongbin，Liu Changhuan.Stability analysis and PI controller tuning for a speed-sensorless vector-controlled induction motor drive[C].IECON 2004，IEEE，Busan，2004：2-6.
[2] Lennart Harmefors.Instability phenomena and remedies in sensorless indirect field oriented control[J].IEEE Trans.on
Power Electronics，2000，15(4)：733-743.
[3] CADE M.Improvement of induction machine stability by modulation techniques[J].IEE Proceedings: Electric Power Applications，1994，141(6)：347-352.
[4] Marek Budzisz，Zbigniew Nowacki.Stabilization procedures based on fuzzy inference algorithms for PWM drives[C].
IAS 1995，IEEE，Orlando，1995：1663-1667.
[5] 王庆义，尹泉.一种改善VVVF变频调速系统稳定性方法[J].电机与控制学报，2007，11(2)：138－142.
[6] COLBY R S，SIMLOT A K，HALLOUDA M A.Simplified model and corrective measures for induction motor instability caused by PWM inverter blanking time[C].PESC 1990，IEEE, San Antonio, 1990: 678-683.
[7] MOSSKULL H.Some issues on stabilization of an induction machine drive[C]. CDC 2004, IEEE, Nassau, 2004: 4441-4446.
[8] Lazhar BEN-BRAHIM. Improvement of the stability of the v/f controlled induction motor drive systems[C]. IECON
1998, IEEE, Aachen, 1998: 859-864.
[9] 李红梅，李忠杰，刘良成.逆变器供电下异步电机低频振荡现象的研究[J]. 电工技术学报, 2000, 15(3): 16-19.
[10] 徐国卿, 张奕黄, 郝荣泰. 逆变器供电感应电机稳态性能仿真的研究[J]. 中国电机工程学报，1999，19(9)：1-5.