摘  要： 基于K-means算法思想改进蚁群聚类算法聚类规则，提出一种新的K-means蚁群聚类算法，并通过实验验证其聚类效果；引入具有全局最优性的支持向量机SVM，取各类中心附近适当数据训练支持向量机，然后利用已获模型对整个数据集进行重新分类，进一步优化聚类结果，使聚类结果达到全局最优。UCI数据集实验结果表明，新的算法可以明显提高聚类质量。
关键词： K-平均算法；蚁群算法；聚类；支持向量机

    聚类是数据在算法的指导下进行无人监督的分类。以K-means[1]和 K-medoid[2]为代表的划分法是常用聚类算法中的一种。常用聚类算法多面向数值属性，而蚁群聚类算法（AntClust）[3-4]能处理任意类型的数据，具有强鲁棒性和适应性，但其聚类结果受数据集大小和参数影响较大，针对这些问题，本文首先使用K-means算法思想改进蚁群聚类算法规则，提出一种新的K-means蚁群聚类算法(KM-AntClust)，使聚类中数据归属有更合理的判定依据，使聚类结果局部最优。KM-AntClust继承了AntClust的优势，且从距离的角度明了地反映蚂蚁与巢的归属关系，使聚类有合理的理论支撑，聚类效果得到提高。但K-means算法收敛准则的主观性及聚类过程中心的累积误差，虽然使各类中心附近的数据能找到最优的归属，但离类中心较远的数据因误差累积不一定都能找到最佳归属，降低了聚类效果。支持向量机SVM是在统计学理论的VC维理论和结构风险最小化原理基础上发展起来的一种新的机器学习方法，具有适应性强、全局优化、训练效率高和泛化性强等优点，其全局最优性弥补了K-means算法的不足。为此在KM-AntClust基础上引入SVM，以各类中心为基准选取适当数据训练支持向量机，然后利用已获模型对整个数据集进行重新分类，从而使聚类结果达到全局最优。UCI数据集实验结果表明新算法的聚类效果得到了进一步提高。
1 蚁群聚类算法简介
    Labroche等提出的蚁群聚类方法AntClust[3-4]利用化学识别系统原理聚类。它不需假设对象的表示，仅用相似度sim(i，j)表示对象i和j的关系。每只人工蚁均有标签Labeli、基因Genetici、模板Templatei[5]以及两个判断参数Mi、Mi+。算法规则如下：
    (1)两只无巢蚂蚁相遇时创建一个新巢；
    (2)无巢蚂蚁与有巢蚂蚁相遇则将无巢蚂蚁归到对方所属巢中；
    (3)两只同巢蚂蚁i、j相遇，若相互接受，则增大Mi、Mj和Mi+、Mj+的值；
    (4)两只同巢蚂蚁i、j相遇，若互不接受，则减小Mi、Mj和Mi+、Mj+的值并将M+值小的蚂蚁移出巢；
    (5)两只不同巢蚂蚁相遇并相互接受则将两巢合并；
    (6)若不出现以上各情况，则不做任何操作。
2 使用K-means优化蚁群聚类模型
2.1 蚁群聚类算法聚类质量不高原因分析
    蚁群聚类算法具有较好的鲁棒性和适应性，但其聚类结果不稳定，主要原因如下：
    (1)规则(4)依据Mi+判断踢出蚂蚁。根据算法思想，Mi+为随机量， 其值不仅与蚂蚁所属巢规模有关，还与循环次数相关。Mi+是蚂蚁i被巢成员接受的程度，而不是反映蚂蚁与巢的依存关系，Mi+大并不能说明此巢是蚂蚁i的最优归属，故依此踢出蚂蚁产生累积误差导致聚类质量降低。
    (2)循环迭代参数Iter和删除概率Pdel的设置。循环次数NBIter=Iter×N不足[5]，数据覆盖率低；太大导致过学习，聚类效果均受影响。参数Pdel太大聚出的类数目较少，相反则类过多，影响聚类质量。因此，参数Iter和Pdel的确定是保证聚类质量的重要环节。
2.2 使用K-means改进蚁群聚类规则
    K-means聚类算法基于误差平方和最小准则，聚类结果通常不受初始中心的影响，较为稳定。对于大数据集，其强伸缩性和高效性常使聚类结果以局部最优结束。
    引入K-means算法改进聚类规则，优化后的算法简称KM-AntClust。设di为蚂蚁i到其所属巢中心的距离，规则改进如下：
    (1)两只无巢蚂蚁i、j相遇时创建一个新巢并计算巢中心；
    (2)无巢蚂蚁i与有巢蚂蚁j相遇则将蚂蚁i归到蚂蚁j所属巢中并更新该巢中心；
    (3)同巢互不接受的两只蚂蚁i、j相遇时，计算di、dj，将d值大的蚂蚁踢出巢并更新巢中心；
    (4)两只不同巢的蚂蚁相遇且相互接受时，将两巢合并并更新巢中心；
    (5)若不出现以上各情况，则不做任何操作。
3 使用SVM优化K-means蚁群聚类算法
3.1 支持向量机SVM
    支持向量机[6-7]SVM是在统计学理论的VC维理论和结构风险最小化原理的基础上发展起来的一种新的机器学习方法。它的基本思想是将输入空间通过一种非线性变换映射到一个高维的特征空间，然后在这个新的高维特征空间中求解原始问题的最优解[8-9]。
3.2 使用SVM优化K-means 蚁群聚类算法
    K-means蚁群聚类算法继承了蚁群算法的优势，且从距离的角度更明了地反映了蚂蚁与巢的归属关系，摒弃了蚁群算法随机的判断条件，使聚类有合理的理论支撑，聚类效果得到提高。但是，K-means算法本身也存在缺点，源于其收敛准则主观设定，聚类过程中心重复计算更新，使各类中心附近的数据能找到最优归属，而离类中心较远的数据因误差累积效应找到最佳归类的性能减弱，从而使聚类结果达到局部最优，影响聚类的效果。
    SVM的强适应性、全局最优性等优点弥补了K-means算法的不足。在已聚出类结果的基础之上再引入支持向量机，对所聚类结果以类中心为基准选取适当数据训练支持向量机，利用获取的模型对整个数据集进行重新测试与分类，从而使得聚类结果达到全局最优。
4 实验及结果分析
4.1 实验平台、数据集及度量标准
    实验平台：PC配置：Pentium 4，2.4 GHz CPU，512 MB内存；Windows XP操作系统；使用VC算法编写。数据集采用UCI公共数据库提供的数据集Iris、Breast-cancer 和KDDCUP。
    聚类性能评价采用了参考文献[10]中介绍的F-measure方法。F-measure组合了信息检索中查准率(precision)和查全率(recall)的思想。一个聚类 j 相对于分类i的 precision和recall定义为：


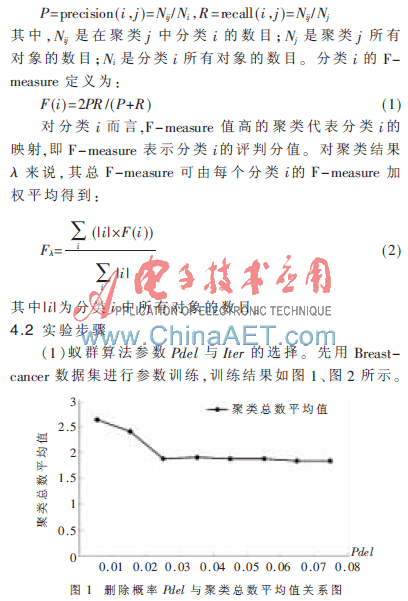
    从图1可知当Pdel≤0.06 时，聚类总数平均值越来

 
    参考文献[11]中说明数据集Iris用于聚类时可作两类处理。从表1可知，与AntClust相比较，KM-AntClust获得更好的聚类效果，其F-measure平均值均比AntClust的高，最高达到了0.988 722；聚类总数也越接近数据集原始分类。而SVM-KMAntClust使得聚类效果得到了进一步提高，其F-measure平均值均比前两种算法的高，有的甚至能全部正确分类，F-measure平均值为1，聚类总数与数据集原始分类数相差甚小。             
    本文对蚁群聚类算法进行研究后，首先提出一种新的K-means蚁群聚类算法(KM-AntClust)，使用K-means算法改进蚁群聚类算法规则，解决了AntClust存在的聚类判断条件随机的问题，提高了聚类效果。受K-means算法局部最优限制，为获取更佳聚类效果，本文在KM-AntClust聚类结果基础上引入支持向量机SVM，选取适当数据训练SVM分类机，然后利用已获模型对整个数据集进行重新分类，充分发挥SVM的强适应性和全局最优性，使得聚类结果达到全局最优。AntClust与K-means算法结合继承了AntClust的优点，同时保证了类的稳定性；AntClust与SVM结合使聚类效果全局最优时也扩大了SVM的应用领域。实验结果表明，三者相结合聚类质量得到了进一步的提高。
参考文献
[1] QUEEN J M.Some methods for classification and analysis  of multivariate observations[C].Proc. of the 5th Berkeley Symp.On Math Statist，1967：281-297.
[2] KAUFMAN J，ROUSSEEUW P J.Finding groups in data：an introduction to cluster analysis[M].New York：John Wiley & Sons，1990.
[3] LABROCHE N，MONMARCHE N，VENTURINI G.A new clustering algorithm based on the chemical recognition system of ants[C].Proc of 15th European Conference on Artificial Intelligence(ECAI 2002)，Lyon FRANCE，2002：345-349.
[4] LABROCHE N，MONMARCHE N，VENTURINI G．Web sessions clustering with artificial ants colonies[EB/OL].(2002-02)[2006-01-12].
[5] LABROCHE N，MONMARCHE N，VENTURINI G.AntClust：ant clustering and Web usage mining[C].GECCO 2003：25-36.
[6] VAPNIK V.The nature of statistical learning theory[M]. New York：Springer-Verlag，1995.
[7] CORTES C，VAPNIK V.Support vector networks[J].Machine  Learning，1995(20)：273-297.
[8] 白亮，老松杨，胡艳丽.支持向量机训练算法比较研究[J].计算机工程与应用，2005，41(17)：79-84.
[9] 沈翠华，刘广利，邓乃扬.一种改进的支持向量分类方法及其应用[J].计算机工程，2005，31(8)：153-154.
[10] YANG Y,KAMEI M.Clustering ensemble using swarm intelligence[C].IEEE SWRFB intelligence symposium. Piscataway，NJ：IEEE service center，2003：65271.
[11] KANADE P M，HALL L O.Fuzzy ants as a clustering concept[C].Proc of the 22nd International Conference of the North American Fuzzy Information Processing Society，2003：227-232.