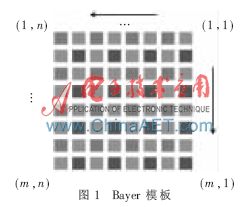
大部分成像设备都使用单板的图像传感器，其在光电二极管和镜头之间利用彩色滤光片阵列CFA(Colour Filter Array)获取图像数据，这样传感器输出的每个像素点只含有红、绿或蓝中一种颜色分量的马赛克图像[1]。为了获得全彩色图像，需要用其领域像素的信号近似计算出被滤掉的另外两种颜色分量，该过程又称颜色插值[2]。CFA的排列方式主要有Bayer、Mosaic和Stripe等[3]，其中应用最广泛的排列方式由Bayer博士发明，为大部分单板传感器使用，称为Bayer模板。其每帧图像的数据格式的排列如图1所示。

    图1中右上角的(1，1)位置作为图像数据的起始点，每帧大小为n×m。使用硬件实现插值运算时，注意Bayer模板中数据的排序方向需和硬件结构中的数据排序一致。

    CFA的插值算法很多，但是基于硬件实现的大多是简单的算法，应用最广泛的是双线性插值法[4]。Bayer模板中双线性插值算法原理非常简单，通常取3×3大小的模板，其中心像素缺失的另外两种颜色的分量用其邻域中同通道分量的平均值代替，其算法简单、运算速度快、硬件实现容易。但由于在插值计算的过程中没有区分图像的边缘，其恢复出的图像效果并不理想，边缘和细节的信息损失较明显。
    本文将介绍Bayer模板的双线性插值算法的改进及其在FPGA中的实现。


    从整个双线性插值计算的过程可知，恢复被滤除的像素时没有考虑图像边缘的变化，只是简单地利用了中心像素的邻域同通道的分量值进行了加和平均，相当于对要恢复的分量使用了均值滤波器。这样虽然会得到平滑的图像，但也造成图像的边缘和细节模糊。
1.2 改进的3×3模板的双线性插值算法
    为了克服双线性插值算法带来的边缘模糊的问题，Laroche 和Prescott 提出了一种基于梯度的边缘导向(edge2 directed)插值算法[5]。插值过程中，首先比较水平方向上和垂直方向上梯度的大小，插值时取梯度值小的方向上的像素点作为估计点计算当前像素未知色彩的值，可避免跨边缘颜色插值导致边缘模糊。由于人眼对绿色较为敏感，为了尽量减少算法复杂度，该算法主要对恢复缺失的G分量的两种排列方式(即图4和图5)时，使用了边缘导向的算法，而恢复缺失的R或B分量则用双线性插值法计算并由G分量修正得到。在边缘导向的算法中，使用了5×5模板，同时在插值计算中，利用了其他的颜色通道即G分量的信息。
    根据边缘导向插值算法的思想，原有的3×3模板不变，无需使用不同像素的通道信息。恢复缺失的G分量插值时考虑邻域G分量像素梯度变化。当插值恢复缺失的R或B分量时，引进邻域同通道已知像素的对角线梯度信息，进一步保留图像的边缘细节信息。因此，对图4和图5两种排列情况的双线性插值算法进行改进，对应公式修正如下：
 

2 硬件实现
2.1 硬件系统架构
    以FPGA芯片为核心的处理单元具有速度快、效率高、低功耗等特点，本算法使用FPGA完成图像数据的读取、Bayer模版的图像插值，既节省了硬件资源，又提高了系统整体效率。
    系统的前端为采集图像数据的CMOS图像传感器，其中FPGA读取Bayer模板图像数据，经FPGA内部硬件构成的3×3模板，完成图像数据的插值还原，最后传输给DSP。其硬件系统如图6所示。

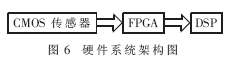
2.2 FPGA中3×3插值模板的硬件结构
    改进的插值算法是基于3×3模板，计算一个中心像素点最多用到相邻2行和2列的像素数据，无需存储整帧实时图像数据，只需缓存３行数据。使用结合FPGA硬件结构的FIFO_DFF的算法模型[6]，即可在FPGA中实现此3×3插值模板，其中构成插值模板的FIFO_DFF硬件结构如图7所示。

    这样无需外部存储设备，在FPGA中就可以根据插值计算公式使用该硬件结构构成的矩阵计算中心像素  P(2，2)的RGB分量的值。需要指出的是，在处理边界像素时也会和其他大小的模板一样不可避免地产生边界效应，当矩阵的第一行没有数据时即开始计算，相当于在此时矩阵中心的第一行数据前面补零；当矩阵中最后一行没有数据读进时的插值计算，相当于在此时矩阵中心的最后一行数据后面补零。可以看出，3×3模板插值时要比5×5模板的边界效应少2行2列。补零后，原Bayer模板的每帧图像数据的起点被移动，式(1)中的x和y也相应变化。因此，3种像素排列规律对应的公式需要根据变化的x和y做相应调整。
3 实验结果
    在CMOS传感器的控制参数和光源条件同等的条件下，利用FPGA构成的3×3硬件模板中分别使用双线性插值算法和改进的双线性插值算法对同一幅彩色广告图片进行拍摄，得到彩色图像数据如图9和图10所示(实际图像数据为2 592×1 944像素大小，这里只选取其左上角部分内容)。

    显示边缘和细节的两幅图进行比较，同时联系各自的彩色图像的色彩信息，可以直观得出：改进插值算法后的图像中右上角的绿色花朵的颜色更加接近实物，色彩鲜艳，其边缘和细节也保留得相对完整，这是式(10)和(12)恢复绿色分量时对同通道的水平和垂直分量进行边缘检测后再插值还原的结果体现。
    同样对图像中间商品名称的红色字和蓝色字分别比较，也可直观得出，改进插值算法的图像中的红色和蓝色更加接近实物，相应的边缘和细节也保留得更多，这是式(11)和(12)分别恢复红色和蓝色分量时使用同通道对角线分量进行边缘检测后插值还原的结果体现。
    对单板CMOS传感器采集的Bayer模板图像数据插值还原时，利用FPGA内部硬件资源构成3×3插值运算模板，减小了其他插值模板所产生的边界效应，无需增加外部存储器，降低了硬件开销。同时，充分考虑Bayer模板图像数据提供的边缘变化信息进行插值还原，与传统的双线性插值算法相比，为后续分析和处理以及最终的结果提供了更加准确和丰富的色彩，并得到了图像中目标物体的更多边缘和细节信息。
参考文献
[1] 周红艳.数码图像中莫尔条纹去除算法的研究[D].上海：上海交通大学，2008.
[2] 彭俊，高伟.基于FPGA的Bayer图像彩色恢复快速算法研究及实现[D].北京：中国科学院研究生院，2007.
[3] 邱菊.基于插值算法的去彩色摩尔纹效应的研究[D].南京：南京理工大学，2009.
[4] 李渊渊，孟伟.一种用硬件实现的Bayer格式图像恢复算法[D].吉林：长春光学精密机械与物理研究所，2009.
[5] 贺钦，刘文予.数字图像传感器颜色插值算法研究[D].武汉：华中科技大学，2007.
[6] 潘胜达.超分辨率传像光纤束成像算法的硬件实现研究[D].上海：上海海事大学，2009.