对于大多数应用，知道传感器节点的位置是至关重要的。无线传感器网络节点定位算法可以分为两类[1-2]：基于测距技术的定位（Range-based）和无需测距技术的定位（Range-free）。Range-based算法的定位精度在一定程度上依赖于测量技术本身的精度。通常测距误差越小，定位算法获得的定位精度越高。常见的测距方式包括TDOA、AOA、RSSI、TOA等[2]。Range-free算法则无需专门测量节点间距离和角度信息，仅根据网络连通性等信息即可实现。由于功耗和成本因素，并且大多数应用对定位精度的要求并不高，无需测距的定位算法也具有很大的使用空间，典型的无需测距的算法有APIT算法[3]、DV-hop算法[4]、质心定位法[5]、凸规划法[6]等。

    粒子群优化算法[7]PSO(Particle Swarm Optimization)早期是模拟一些简单的社会群落生物，如鸟群、鱼群等模型，是一种基于群体的演化算法。PSO算法简单，易于实现，需调参数少，是解决非线性连续优化、组合优化等问题的有效工具。
    参考文献[8]将粒子群优化算法应用到无线传感器网络的节点定位过程中，根据节点间的测距信息构成目标函数，将节点自定位转化成非线性优化问题，用粒子群优化算法对其进行求解，并且指出在定位精度方面要优于多边定位法、模拟退火算法等。参考文献[9]根据离散线性系统的稳定性理论，推出了保证粒子群优化算法收敛性的参数设置区域，参考文献[10-12]对粒子群优化算法的惯性权重进行了改进,分别提出了线性递减、非线性递减以及反馈动态调节的惯性权重取值策略，提高了算法寻优精度以及收敛速度。本文根据惯性权重对粒子搜索能力的影响，并结合节点间连通性对惯性权重的设置进行改进，使其更加适应无线传感器网络节点定位。
1 粒子群优化算法
    PSO算法在一定区域中随机选取一组位置坐标，作为粒子群的初始粒子。粒子通过代入目标函数来计算适应度，从而得到粒子本身所找到的最优位置Ppbest和整个种群目前找到的最优位置Pgbest，通过更新迭代，最终获得满足要求的最优目标位置。
   
 

    在传统的粒子群优化算法中，未知节点可能存在的区域是根据所有节点布设的范围来估计的，粒子在该区域内初始化并且不断更新，搜索最优位置，对粒子更新提供的约束信息非常有限,经过上述对节点间连通度的利用，很大程度上缩小了未知节点可能存在的区域,为粒子群的初始化、个体最优位置Pipbest和群体最优位置Pgbest的更新提供了更加精确的范围限制。改进后算法的粒子种群可以在相交区域内随机选取,利用区域?椎的中心坐标作为Pgbest，在粒子的更新阶段,相交区域可以为粒子更新速度提供约束条件，要求更新后粒子不应跳出相交区域。
2.2 改进惯性权重设置
　　惯性权重w的大小体现了对粒子当前速度继承的程度。参考文献[10]指出较小的w可加强局部搜索能力，而较大的w则有助于在全局范围内搜索，并且将惯性权重w设计为随迭代次数线性递减的函数，在算法的初期使用较大惯性权重以跳出局部最优解，而在后期则使用较小惯性权重，提高局部搜索能力以加快收敛速度。即：

    根据节点连通性的约束，在一定程度上缩小了未知节点可能存在的区域。在比较小的区域内利用粒子群优化算法估计未知节点坐标，选用较大的w可能使粒子跳出有效区域，此时更加倚重较小的w来加强局部搜索能力，而式(6)的惯性权重下降速率是恒定的，不利于更快速准确地获得最优位置估计。因此本文将w设计成前期较大的惯性权重下降速率较快、较小的惯性权重下降速率较慢的非线性递减函数。

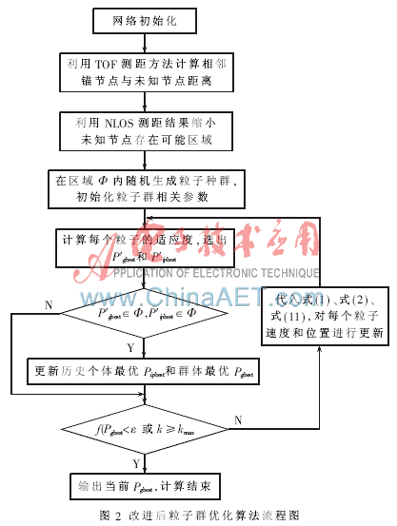
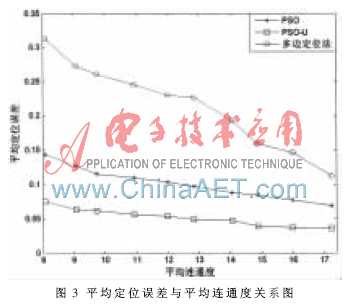
    为了表述方便，将本文提出的改进后粒子群优化算法记作PSO-U，并与前文提到的PSO、多边定位法[2]等位置估计算法进行性能比较。图3是在锚节点密度设定为30%，通过调节节点通信距离来控制平均连通度变化的情况下，对三种算法平均定位误差的比较。图中随着节点平均连通度的增大，各算法的平均定位误差逐渐下降，其中PSO-U算法的下降幅度最小，相对于另外两种算法受平均连通度变化的影响较小，在较小连通度的情况下就可以达到比较高的定位精度。图4是在平均连通度设定为13，锚节点密度从20%线性增加的情况下，对三种算法平均定位误差的比较。图中各算法的平均定位误差随着锚节点密度的增大而逐渐变小，相对于平均连通度的变化,锚节点密度对平均定位误差的影响较小。

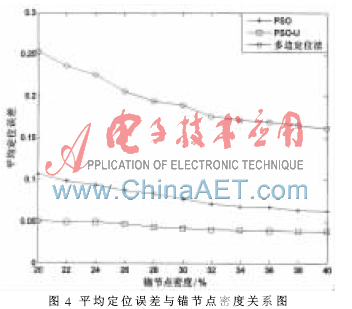
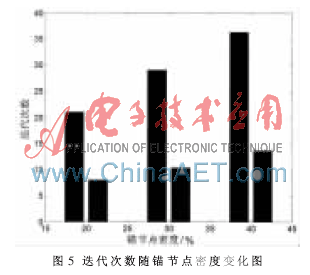
    粒子群优化是一种迭代搜索方法，迭代次数是该算法计算量的重要体现，以下对改进后粒子群优化算法的迭代次数进行仿真分析。图5是锚节点密度分别取20%、30%、40%的条件下，PSO-U和PSO的平均迭代次数比较。从两图中可以看出，本文提出的PSO-U算法的平均迭代次数明显小于PSO算法。但是综合分析改进前后的粒子群优化算法，PSO-U算法需要对相交区域进行估算，这相对于PSO算法是额外的计算量，并且惯性权重在形式上要更为复杂。因此，整体来看，本文提出的PSO-U算法在定位精度上有明显的优势，但在算法复杂度上有所增加，适用于对精度要求较高的WSN应用中。

    本文将粒子群优化算法应用到节点定位过程中，通过对惯性权重的分析，对基于粒子群优化的节点定位算法进行了改进。首先利用节点间的连通性估计未知节点可能存在的约束区域，然后对粒子群优化算法的惯性权重的设置进行了优化。通过仿真比较，改进后算法在定位精度方面有明显改善，并且受节点分布的影响较小。由于粒子群优化算法通过迭代方式搜索未知节点的最优位置，在测距误差较大、参数设置不理想等情况下，其计算量会有比较明显的增加。
参考文献
[1] KRISHNAMACHARI B. Networking wireless sensors[M].New York: Cambridge University Press, 2005.
[2] 孙利民, 李建中, 陈渝,等. 无线传感器网络[M]. 北京:清华大学出版社, 2005.
[3] TIAN H, CHENGDU H, BRIAN M B, et al. Range-free localization schemes in large scale sensor networks[A]. In: Proceedings of the 9th annual international conference  on mobile computing and networking (MobiCom’03)[C], San Diego, California, USA, 2003:81-95.
[4] NIEULESEU D, NATH B. DV based positioning in ad hoc networks[J]. Journal of Telecommunica- tion Systems,2003,22(1):267-280.
[5] BULUSU N, JOHN H, ESTRIN D. GPS-less Low cost outdoor localization for very small devices[J]. IEEE Journal of Personal Communications, 2000,7(5):28-34.
[6] DOHERTY L,PISTER K S J,GHAOUI L E. Convex position estimation in wireless sensor networks-[A]. In: Proceedings of the IEEE INFOCOM 2001[C], 2001(3):1655-1663.
[7] KENNEDY J, EBERHART R C. Particle swarm optimization[C]. Proceedings of IEEE International Conference on  Neural Networks, Perth, Australia, 1995:1942-1948.
[8] GOPAKUMLAR A, JACOB L. Localization in wireless sensor networks using particle swarm optimization[C]. IET International Conference on Wireless, Mobile and Multimedia Networks, 2008(1):227-230.
[9] 林卫星,陈炎海.一种快速收敛的改进粒子群优化算法[J].系统仿真学报, 2011,23(11):2406-2411.
[10] SHI Y H, EBERAHRT R C. Parameter selection in particle swarm optimization[J]. Lecture Notes in Computer Science, 1998, 47(14): 591-600.
[11] CHATTERJEE A, SIARRY P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers & Operations Research, 2006,33(3):859-871.
[12] 焦巍, 刘光斌. 基于多样性反馈的粒子群优化算法[J]. 计算机工程, 2009,35(22):202-204.