跳频通信具有良好的抗多径、抗衰落、抗干扰、低截获率和易于组网等特点，因此其在军事和民用通信方面得到了极大的应用和发展。

    由于多频率分量信号处理中被广泛使用的魏格纳威尔分布WVD(Wigner-Ville Distribution)会产生交叉项问题，严重影响信号检测结果，因此许多研究采用改进的WVD方法[1-3]，这些改进算法虽然能降低交叉项的影响 ，但运算量过大，且有的算法会导致时间分辨率及频率分辨率受到严重影响。参考文献[4]提出了一种基于自回归自适应谱估计模型的跳频信号检测方法;参考文献[5]提出利用信号STFT的结果得到其峰值序列来进行跳频信号的跳周期估计；参考文献[6]采用了时频分析与图像处理相结合的算法，有效地通过图像分割等技术提取出了跳频信号，但由于未考虑到实际环境中所存在的噪声干扰等问题对跳频信号检测的影响，使其实用性受到局限。
    本文提出用短时傅里叶变换(STFT)对跳频信号进行分析，利用现在较为完善的图像处理技术与时频分析相结合，滤除杂散噪声及定频、突发号，再根据时频图中信号在时间轴和频率轴上的投影求出频率集，利用跳时刻差分的均值来估计跳周期并通过实验给出了估计性能。并且目前大多数文章所提出的方法都只是建立在仿真分析的基础上，缺乏实际应用验证。而本文提出的方法已应用于实际产品中，其稳定性和精度均能满足需求，具有较高的实际意义。
1 跳频信号的检测及分析
1.1 短时傅里叶变换
    跳频信号是一种非平稳信号，传统的傅里叶变换对它的处理具有信号的时域与频域信息不能同时局部化等局限性。而时频分析[7]作为分析时变非平稳信号的有力工具，近年来受到越来越多的重视，已成为跳频通信研究中常用的分析手段。其中STFT计算量小、时频聚集性较好，从时频图中可以较为明确地分析信号特征，应用最为广泛。

    根据W.Heisenberg不确定性原理，短时傅里叶变换的时间分辨率和频率分辨率互相矛盾，应当根据实际情况来考虑时间分辨率及频率分辨率的大小。对非平稳信号，若信号变化剧烈，要求窗函数有较高的时间分辨率；而波形变化比较平缓时，则要求窗函数有较高的频率分辨率。因此，窗函数的选取十分重要，窗越宽，时间分辨率越差；反之则会降低频率分辨率。
1.2 对时频图进行图像处理
    通过短时傅里叶变换得到的时频图，可以将其视为一幅二维图像。复杂的电磁环境中存在许多噪声会对跳频信号的检测造成较大干扰，而这些噪声信号在时频图中的表现形式各有不同。在时频图中不同频率上彼此衔接的短线段为跳频信号，每一段短线段即为一跳;图中除跳频信号外，在同一频率连续出现的长线段为定频信号；一系列较细的斜线段为扫频信号；由噪声的随机性产生的雾态噪声，在时频图上为随机分布的零散能量。因此，从实际环境中剔除噪声信号演变成为对时频图进行图像相关处理。
    数学形态学是基于集合论的图像处理分析方法，可以保持所需图形的基本形状特性，并除去不相干的结构，并且可以大大提高图像分析和处理的速度。本文选用其中的开、闭运算来对时频图进行滤波处理。


    为了从复杂的信道环境中提取出跳频信号，应对时频图进行进一步的形态学滤波处理。首先进行图像开处理，以滤除雾态噪声。通过实验验证，开运算的结构元素选择宽625个点，高1个频率分辨率的矩形效果较好，经过开处理后的时频图如图2所示。其次进行图像闭处理，提取定频信号。闭运算的结构元素选择宽375个点，高1个频率分辨率的矩形窗。经过闭运算后提取出来的定频信号。这样的结构元素能够抑制谱图中的波谷噪声，填平杂散负脉冲；也符合跳频信号形态特征，在一定程度上恢复了由去干扰处理导致的信号形态缺失。

    再将除去杂散噪声后的时频图与提取出的定频信号进行式(7)的运算，便可以提取出跳频信号，如图3所示。可以看出，通过形态学处理，噪声剔除效果较好，且基本未对原有的跳频信号产生影响。在求取跳周期时，由图3跳频信号时频图可以看出，信号存在第一跳和最后一跳两个不完整的跳频周期，它们会对跳频周期的估计产生较大的影响，而这两跳之间的跳频信号都是完整的,对跳频周期的估计没有影响。所以在估计跳频周期的过程中，用第一跳与最后一跳之间的跳时刻的差分均值求取跳周期。
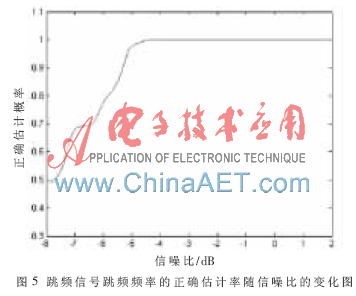
    为验证本文方法在不同信噪比的情况下对跳频参数估计性能的影响，对[-8 dB,2 dB]之间的不同信噪比下的信号分别进行100次实验，得到跳频信号跳周期的正确估计率随信噪比的变化图，如图4所示。从图4中可以看出，当信噪比高于-3 dB之后，对跳频信号跳周期的正确估计率达到95%以上。跳频信号跳频频率的正确估计率随信噪比的变化如图5所示。由图5可知，当信噪比高于-5 dB之后，对跳频信号跳频频率的正确估计率达到98%以上。

    本文在实际应用背景下提出了一种跳频信号检测及参数估计的方法，理论分析和现场应用表明，本文方法能有效消除复杂的电磁环境中所存在的噪声干扰，且估计精度较高，运算量小，把算法应用于实际工程中，更具有工程价值。
参考文献
[1] 赵俊,张朝阳，赖利峰,等. 一种基于时频分析的跳频信号参数盲估计方法[J].电路与系统学报, 2003,8(3)：46-50.
[2] 冯涛,袁超伟. 跳频信号的时频分析新方法[J].北京邮电大学学报, 2010,33(3):10-14.
[3] 陈超,郝雁中,高宪军,等. 基于WVD改进算法的跳频信号参数估计[J].吉林大学学报,2010,28(2):124-130.
[4] 黄东巍,邵定蓉,李暑坚. 基于自适应谱估计的跳频捕获技术[J].北京航空航天大学学报,2006,32(5):540-543.
[5] 严超会,汤建龙. 跳频信号的跳周期估计[J].信息与电子工程,2011,9(1):74-77.
[6] Xu Mankun, Ping Xijian, Li Tianyun, et al. A new time frequency spectrogram analysis of FH signals by image enhancement and mathematical morphology[C]. Fourth International Conference on Image and Graphics, 2007:610-615.
[7] BARBAROSSA S, SCAGLIONE A. Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributions[C].First IEEE Signal Processing Working on Signal Processing Advances in Wireless Communications, 1997:213 -216.
[8] 朱文贵, 戴旭初, 徐佩霞.  一种跳频信号参数估计的方法[J].小型微型计算机系统,2008,29(4):761-764.