近年来，随着宽带信号在通信、雷达等领域得到广泛应用，宽带信号来波方向(DOA)估计已成为目前阵列信号处理领域中的热点，对于目标识别、电子对抗等有着重要意义[1-2]。

    空间谱估计的实质是利用远场信号到达各个阵元之间的相位差来计算信号的DOA。目前，测向阵列多采用均匀线阵，其具有结构简单、易于实现等优点。为了使阵列能在180°范围内无模糊测向，均匀线阵的间距必须限制在半波长内。但均匀线阵也有一些不足，例如：对宽带信号进行测向时，由于阵元间距与波长之比随着频率的降低而降低，导致测向的精度相应降低；对功率较小的信号，需要增加阵列孔径才能有效测向，这会导致阵列安装出现问题；阵元间的互耦效应随着阵元间距的减小而增加[3]，当利用对高频信号进行DOA估计的均匀线阵对低频信号进行DOA估计时，由于阵元间距与波长之比变小，互耦效应会严重影响测向性能。为提高均匀线阵测向精度，学者们提出利用非均匀线阵测向，例如最小冗余线阵(MRL)[4]、最大连续阵列(MCL)、最小间隙阵列[5-6]等。但是，这些阵列多是基于被测信号为窄带信号这一前提假设的，并未考虑宽带信号时的情况。
    本文提出了一种基于改进粒子群算法(PSO)的阵列结构设计方法，通过优化阵元位置来提高阵列的测向性能，改进算法与标准PSO算法相比提高了搜索效率，同时，设计方法既满足了测向无模糊的要求，与均匀线阵相比，又提高了阵列的测向性能。
   

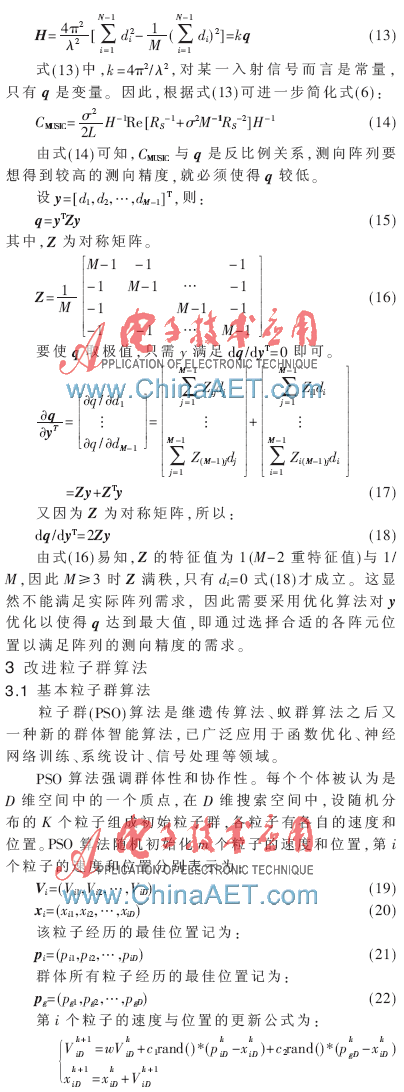    (23)

式(23)中，加速因子c1、c2为非负常数，它们决定pi与pg的影响程度，w为惯性权重。迭代终止条件一般为最大迭代次数或粒子群的群体最优适应度满足适应阈值[11]。
3.2 改进粒子群算法
    在基本PSO算法中存在粒子易于过早收敛于局部极值的缺点。由于PSO这种随机的基于群体搜索的优化算法必须测试空间内各点才能保证收敛于全局最佳点，因此算法的计算量很大，难以实现[12]。如果在搜索初期能够使得粒子尽可能地飞跃整个搜索空间，以期获得更好的多样性，则可能摆脱局部极值的干扰。
    加速因子c1、c2决定了粒子本身经验信息和其他粒子信息对粒子运动轨迹的影响，反映了粒子群之间的信息交流，分别调节向全局最好粒子和个体最好粒子方向飞行的最大步长。如果步长太大，则可能导致突然向目标区域飞去或飞过目标区域；如果步长太小，则可能使粒子远离目标区域，即粒子的速度没有得到有效的控制。合适的c1、c2能够加速收敛且不易陷入局部最优,通常令其值均为2[13]。对于加速因子的取值，许多文献给出了不同的建议，如参考文献[14]就给出了加速因子没有必要固定为2的建议。
    针对上述问题，可令粒子在搜索初始时刻应用较大的c1值和较小的c2值，使粒子能够飞跃整个搜索空间，增加粒子的多样性。随着迭代的增加，使得c1值降低和c2值增加，加强粒子向全局最佳点收敛的能力。

3.3 阵列结构的优化
    从上述分析可知，优化的前提条件为：
    (1) 测向阵列在规定的工作频率和测向范围内测向精度要高，且不存在测向模糊。
    (2) 对式(15)优化时，只是对各阵元位置的范围进行了约束，考虑到实际环境的限制，还需对阵元间距有约束。设阵元最小间距为dmin。
    在上述条件下，对式(15)进行优化，对得到的系列较优结果依次进行验证，检验其是否满足阵元间距限制和测向不模糊的条件，直至找到满足条件的结果。具体过程如下：
    (1) 初始化阵列参数。根据设计要求设置阵元数M、阵元最小间距dmin、阵元最大位置量dmax、算法的迭代次数m。
    (2) 粒子群初始化。设粒子群的规模n，在允许范围内随机设置粒子的初始位置p及其速度v。
    (3) 按照改进粒子群算法中的加速因子c1、c2与式(23)进行粒子迭代，并对粒子位置进行修正，利用式(15)进行优化，在达到迭代次数后停止。
    (4) 对得到的各历史最优粒子，按粒子适应函数值进行升序排列，并按照最小阵元间距dmin淘汰不合格粒子，得到新的历史最优粒子。
　　(5) 按照模糊性条件对步骤(4)得到的新粒子进行依次检验，满足要求，则把该粒子值记为阵元位置值。如果没有发现满足条件的粒子，则设计失败，转到步骤(2)重新初始化条件。

    表2中阵元位置的单位为m。从各阵元位置发现，最小阵元间距小于半波长，与均匀线阵相比有了提高。
    实验3  测向阵列的性能仿真
    对实验1中得到的6元阵列进行测向性能实验。阵列测向频率在25 MHz~100 MHz之间，假设2个窄带远场信号分别从5°和8°入射到阵列上，采用经典MUSIC算法，快拍数为1 024，各阵元接收到的噪声为相互独立、零均值的高斯过程，信噪比为5 dB，入射信号频率从40 MHz开始，以20 MHz为步长变化到100 MHz，进行100次蒙特卡洛实验，分析各频率时的MUSIC谱。实验结果如图1所示。

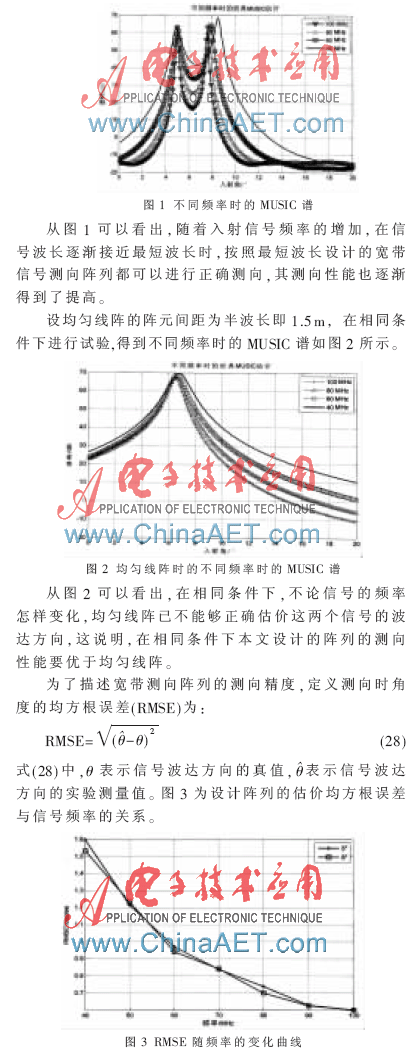
    从图3可以看出,在相同条件下对波达方向为5°、8°的信号测向所得的RMSE进行比较，前者要略大于后者。
    本文通过分析测向模糊的机理，对无模糊测向阵列的结构设计提出了建议。为提高测向精度提出了基于改进PSO算法的阵列位置优化。实验证明，改进PSO算法不仅提高了搜索效率，优化后阵列的最小阵元间距不受均匀线阵中阵元间距不大于半波长的约束,且阵列的DOA分辨率要优于均匀线阵。
参考文献
[1] 张恒利, 赵拥军, 张培峰.宽带信号源数目和DOA快速估计[J].电子对抗,2008(5):10-14.
[2] 赵春晖,李刚,李福昌.宽带测向研究现状及展望[J].哈尔滨工程大学学报, 2006,27(2):290-295.
[3] SVANTESSON T. Mutual coupling compensation using subspace fitting[C]. IEEE Trans. Antennas propagation, 2000: 494-498.
[4] 赵大勇, 陈超, 刁鸣. 基于最小冗余线阵的二维传播算子DOA估计[J].系统工程与电子技术,2011,33(4):724-727.
[5] 于振海,宋石磊,赵国庆.最小间隙阵的插值分析[J].国外电子测量技术, 2006,25(11):31-35.
[6] ABRAMOVICH Y I, SPENCER N K, GOROKHOV A Y.  Positive definite toeplitz completion in DOA estimation for  nonuniform linear antenna arrays[J]. IEEE Trans. Signal Processing, 1999,47(6):1502-1521.
[7] 罗景青.雷达对抗原理[M]. 北京：解放军出版社, 2003.
[8] 王永良, 陈辉, 彭应宁. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2009.
[9] 刘志强,高晓光,杨建伟.宽带测向阵列结构设计方法[J].西北工业大学学报, 2010,28(6):893-897.
[10]    STOICA P, NEHORAI A. MUSIC, maximum likelihood, and cramer-rao bound:further results and comparisons[J]. IEEE Trans. on ASSP, 1990,38(12):2140-2150.
[11]  胥小波,郑康锋,李丹,等.新的混沌粒子群优化算法[J]. 通信学报, 2012,33(1):24-33.
[12]  冯翔, 陈国龙, 郭文忠. 粒子群优化算法中加速因子的设置与实验分析[J]. 集美大学学报, 2006,11(2):146-151.
[13]  杨维,李歧强.粒子群优化算法综述[J].中国工程科学, 2004,6(5):87-94.
[14]  SUGANTHAN P N. Particle swarm optimiser with neigh  bourhood operator[C]. IEEE Press. Evolutionary Computation, 1999(3):1958-1962.