随着现代工业和电力电子技术的飞速发展，各种大功率非线性设备接入电网,使得电力系统产生波动，从而产生高次谐波，造成电网的谐波污染，引起测量误差，增加能耗、破坏设备，并对家用电器产生干扰，甚至会对人们的生命财产安全带来较大影响。谐波检测是谐波抑制和净化电网质量技术的一个重要分支，传统的谐波检测算法最早采用模拟滤波器实现[1]，后来又出现了三相电路瞬时无功功率方法，但不能检出全部谐波电流[2]。自适应谐波检测的优点是对电网电压畸变、频偏及电网参数变化有较好的自适应能力，但其动态响应较慢[3]。傅里叶变换在信号检测时不能解决时域和频域的局部化矛盾,而人工神经网络适合用来分析整数次谐波，但对含有非整数次谐波有一定缺陷，易于限于局部最优[4]。

    典型环节中的二抽取是对偶数坐标位置元素的抽取不同，本算法利用小波系数模极大值原理,同时抽取数组低频、高频段的奇数和偶数坐标位置的元素，避免未抽取的部分和已抽取部分产生信号混叠。抽取后经过BP神经网络的输出为：

2 谐波检测方法
　本文提出谐波检测及补偿方法为：利用小波变换对多频电网谐波信号进行分解，将各次谐波分量分解到不同频带的子频带信号中，构成多个子空间，从中检测出含有基波分量的子频带区域，其余子频带区域均含有谐波分量。对含有各谐波分量的子频带区域的小波分解系数取负数，基波所在区域小波系数不变，利用新得到的小波系数对信号进行重构，则重构信号中除了含有基波分量的区域之外，其余各次谐波分量均己进行了反相。将重构信号和原始谐波信号相减， 则得到谐波补偿信号 [8]。实际应用中，通过谐波检测方法检测出电网中的谐波成分，并通过智能算法计算出谐波补偿信号，将所得到的补偿信号转变成反相PWM，再通过逆变装置注入到电网，即可实现谐波抑制。谐波检测与补偿控制的结构图如图2所示。

    小波分解是将信号按尺度函数和小波函数进行划分，利用小波系数模建立模极大值的特征向量，并对特征量按照隶属函数划分。不同频率的信号根据尺度的不同被划分到不同的频段中，对各频段分别进行奇数和偶数抽取，得到信号细节a(2k)、a(2k-1)和d(2k)、d(2k-1)，从而分离出各次谐波。用3层神经网络对细节信号进行逼近训练，再确定综合滤波器g0、g1，然后用小波逆变换对信号重构，得出各个采样时刻的基波值和谐波值。
3 试验
    在电网中电压和电流的基波频率均为f0=50 Hz，本文选择最常见的含有3、5、7、9次谐波的情况。设单相电压信号的数学表达式为：
    

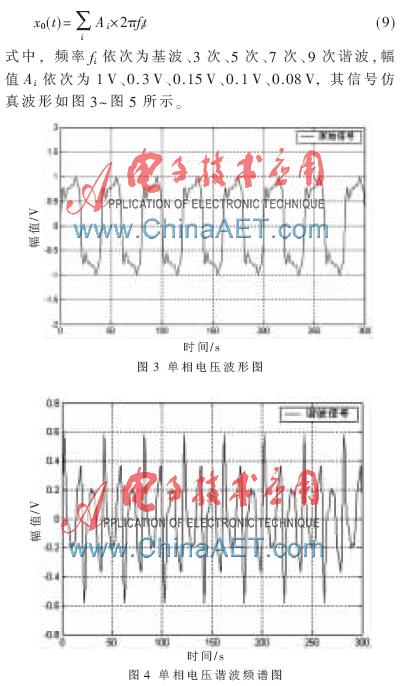
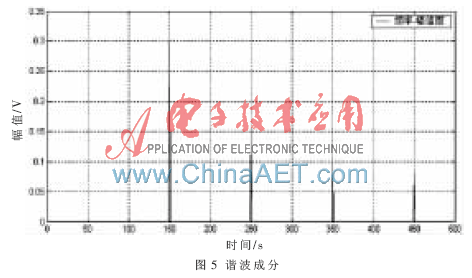
    图3为含高次谐波的电力系统单相电压波形，图4为单相电压波形的频谱图，图5为分离出的谐波成分。小波网络逆变换算法能准确地将给定信号的基波信号和谐波信号分离出来，各尺度体现的频率成分变化趋势各不相同，表明没有出现混叠和泄露现象。使用离散小波变换提取子频带内的信息，利用3层神经网络对信号进行逼近，可以精确地量化谐波信号的频率和幅值。实验数据如表1所示。

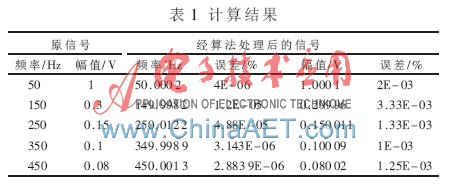
    通过表1可以看出，利用该算法分解出的各次谐波频率值误差率在10-5数量级，幅值的误差率在10-3数量级，完全符合谐波分析的精度要求，从而验证了基于谐波小波分析电力系统谐波分量是可行的。    
    信号通过小波分解到各个尺度空间的细节信号，利用小波系数模极大值可以有效分离出基波和谐波分量，用修正的系数重构原始信号。通过小波分解系数的重构就可以测量电力系统中的各个频带内的谐波频率和幅值。通过算法可以确定出信号中的各次稳态谐波以及谐波的含量，提高分析的可靠性,满足系统对精度的要求，在电力系统谐波检测中具有较好的应用前景。
参考文献
[1] 帅定新,谢运祥,王晓刚.电网谐波电流检测方法综述[J].电气传动,2008,38(8):71-76
[2] 杨君,王兆安,邱关源.一种单相电路谐波及无功电流检测新方法[J].电工技术学报,1996,11(3):42-46.
[3] 何英杰,邹云屏,李辉,等.用于有源滤波器的一种新型谐波检测算法[J].电力电子技术,2006,40(2):56-58.
[4] 戴君.基于小波变换的电力系统谐波分析与检测方法研究[D]. 无锡：江南大学,2008.
[5] 飞思科技产品研发中心. 小波分析理论与Matlab 7实现[M].北京:电子工业出版社,2005.
[6] HAMID E Y, KAWASAKI Z I. Wavelet packet transform for RMS and power measurement[J].IEEE Power Engineering Review,2001,21(9):49-51.
[7] 雷锡社,刘敏.基于神经网络的高精度电力系统谐波分析[J].电测与仪表,2007,44(3)：17-21.
[8] 王兆安, 杨君, 刘进军. 谐波抑制和无功功率补偿[M]. 北京:机械工业出版, 2002.