摘　要： 在分析AES算法的基础上，介绍了该算法各模块的设计实现方法，并将加解密运算结构设计为1个统一的结构。通过对密钥生成算法的分析，将3种密钥长度的密钥生成算法进行了可配置设计，使该设计能够实现加解密功能。该设计通过了FPGA仿真验证，与传统设计方案相比大大减小了硬件资源的消耗。
关键词： 高级加密标准； 统一加解密结构； 可配置密钥生成结构； 现场可编程门阵列

    在信息安全领域，数据加密是一种常用且行之有效的方法。高级加密标准AES[1]算法设计简单，便于硬件实现，是新一代的主流对称加密算法。相对于软件实现，硬件实现加密算法安全性好、计算速度快。本文基于FPGA提出了一种AES算法的可配置设计方法，对数据分组长度为128 bit，密钥长度为128 bit、192 bit和256 bit的加解密运算进行了可配置结构的设计与实现。
1 AES算法介绍
　AES为迭代分组密码算法，对待加密的明文先分组后再加密。明文长度和密钥长度均可以为128 bit、192 bit和256 bit。根据明文长度及密钥长度的不同组合，加密的轮数可以不同[1]。AES算法由加密、解密算法和密钥扩展算法3个部分组成。
1.1 加/解密算法
　加密算法的每一轮由4个变换组成，依次为字节代替、行移位、列混合以及轮密钥加。最后一轮变换与其他轮略有不同，主要是少了列混合变换。解密算法与加密算法相反，每一轮的4个变换为相应加密变换的逆变换，依次为逆字节替代变换、逆行移位变换、逆列混合变换、逆轮密钥加。加解密算法所用子密钥相同，只是使用的顺序刚好相反。
1.2 密钥扩展算法
    圈子密钥是通过密钥扩展算法从初始密钥中获得的，其长度等于分组长度。AES的密钥扩展算法由密钥扩展和密钥选取两部分构成。
    初始密钥经密钥扩展过程产生32Nb(Nr+1) bit的扩展密钥，共包含Nb(Nr+1)=t个4字节的密钥字(其中Nr代表迭代轮数，Nb代表数据分组数，Nk代表密钥分组数，数据和密钥每个分组为32  bit)。扩展后得到的全部密钥字为：w0 w1…wt-1，前Nk个密钥字直接由外部密钥获得，后续密钥字根据初始密钥的长度分为2种情况得到。当密钥长度为128  bit或192  bit时，后续密钥字wi等于其前1个字wi-1与Nk个位置之前的字wi-Nk的“异或”。对于Nk的整数倍位置的字，在“异或”之前，要对wi-1进行1次G变换。G变换的步骤为先进行1次字节循环移位，然后再做1次字节替代变换，最后再“异或”1个轮常数。当密钥长度为256位时，如果Nk=8且i-4是Nk的整数倍，则“异或”之前对wi-1要做1次字节替代变换。
2 AES算法各模块的设计
2.1 S盒的设计
    字节替代变换是关于字节的非线性变换，它将状态中每1个字节非线性地变换为另1个字节，替代(S盒)是可逆的。S盒的传统设计方法是使用VHDL语言中的CASE语句进行描述，但这样实现的S盒将占用大量的逻辑资源，且速度较低，FPGA内部的存储器资源得不到充分利用。为了充分利用FPGA芯片内部的存储器资源，提高运行速度，可将替代的内容存储到FPGA内部的存储器中，根据输入字节的数值进行快速的查表操作。即把输入的8 bit待处理数据作为地址，对应的地址空间中存放字节替代后输出的8 bit数据。对于逆S盒，可以用同样的方法来实现。
2.2 行移位的设计
    行移位是以字节为单位进行的循环移位。由于移位位数是固定的，故可采用直接连线的方式来实现。这样只会占用连线资源，时间仅为线上传输延迟，速度非常快。对于逆行移位，可以采用同样的方法来实现。
2.3 列混合的设计
    由AES列混合变换的原理可知，列混合变换就是输入状态矩阵与1个系数矩阵相乘，此系数矩阵中的元素有3种，分别为16进制数01、02、03。由参考文献[2]可知，可以利用xf(x)算法对其进行快速实现。逆列混合变换的原理类似，其系数矩阵中的元素有4种，分别为16进制数09、0e、0b、0d。同样可利用xf(x)算法对其进行实现，只是乘数较大，需多次使用xf(x)算法，因此逆列混合较之列混合在资源消耗和运算时间上都有所增加。
2.4 密钥加的设计
    由于本设计采用128 bit的数据分组长度，所以密钥加的设计是将2个128 bit数作“异或”运算。因为“异或”的逆运算也为“异或”，所以解密变换的密钥加也为2个128 bit数的“异或”。
3 加/解密运算的统一结构设计
    AES算法加/解密运算过程的相似性是进行统一结构设计的基础。通过分析可知，加/解密运算的变换环节也存在相同或相似性，如S盒变换、行移位变换、密钥加以及密钥生成，这些都可作为统一结构设计的组件。
    S盒变换是该算法硬件实现时最重要的环节，其所占资源在整个算法中的比重很大，对于S盒和逆S盒，它们的输入输出端口都为8进8出，占用的存储资源相同，不同的只是存储空间中的内容。因此在设计中，可让加/解密共用同一个S盒模块，只是在实现加/解密运算时，对S盒中的存储内容进行重新配置即可。S盒的重用可使消耗的硬件资源大为减少。
    对于行移位和逆行移位，其实现仅需占用连线资源，所以两者的单独设计不会造成逻辑资源消耗的增加。且行移位只是以字节为单位进行移位，与字节的值无关。而S盒变换只是改变字节的值,与字节的位置无关。所以两者的执行顺序可以交换。在本设计中，为了使加/解密流程更趋于相同，把解密的逆S盒与逆行移位的位置进行了交换。
    对于“异或”运算，因其逆运算就是它本身，所以在加/解密过程中，2种密钥加运算可以用同一硬件资源来实现。
    在增加了相应的控制信号和选择器之后，加/解密算法可归结为同一个计算流程，如图1所示。

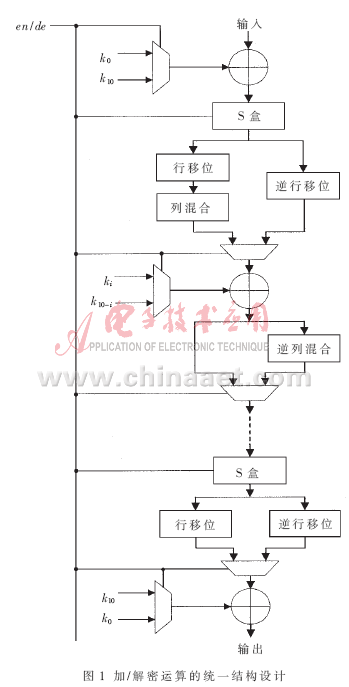
    由于加/解密被归结为同一个计算流程，因此在实现时，两者可共用相同的控制资源。相对于单纯的加密结构，本设计仅增加了逆列混合单元和部分控制资源即实现了加/解密运算的双重功能。
4 密钥扩展算法的可配置设计
    由算法原理可知，128 bit，192 bit及256 bit 3种密钥长度的密钥生成算法各不相同。128 bit密钥长度的密钥生成算法的每1圈流程[3]如图2所示。192 bit密钥长度的密钥生成算法与之类似，只须把每轮的输入输出改为6路即可。

    256 bit密钥长度的密钥生成算法与128 bit和192 bit略有不同，即把第4路输出经过了1个S盒变换，S盒变换的结果再与第5路“异或”，其每1圈的流程如图3所示。

     通过对3种密钥生成算法的分析可知，3种算法的圈函数结构存在很大的相似性，128 bit、192 bit的密钥生成圈函数都可视为256 bit密钥生成圈函数的一部分。因此可以通过对后者进行适当的变形，从而实现128 bit、192 bit密钥长度的密钥生成算法。本文通过在256 bit密钥生成算法圈函数的基础上添加2个必要的数据选择器来实现128 bit与192 bit的密钥生成算法，具体实现结构如图4所示。

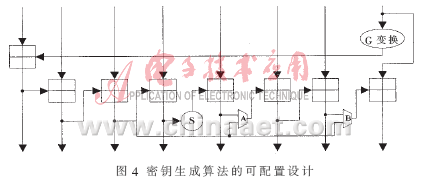
    图中，第3路输出和第5路输出作为选择器A的输入，其输出与第6路输入“异或”。同理，第3路输出与第7路输出作为选择器B的输入，其输出与最后1路输入“异或”。选择器A、B为32  bit的二选一多路选择器。只须对选择器A、B进行控制，便可灵活实现3种密钥生成算法。若要实现256  bit密钥生成算法，使选择器的输出均为上一路的输入即可。若要实现192  bit密钥生成算法，须使A选择器的输出为下一路，B选择器的输出为上一路。同时，圈函数的输入与输出应分别选取除第4路与第5路之外的其他路；若要实现128 bit密钥生成算法，只需使B选择器的输出为下一路。同时圈函数的输入与输出分别选取第1、2、3路和最后一路。
　由以上分析可知，仅通过添加2个数据选择器、3种密钥生成算法便可成为1个算法，易于实现且3种算法还可共用中间结构寄存器资源、控制资源。所以相对于3种密钥生成算法的单独硬件结构设计，本设计所消耗的硬件资源将大大减少。
5 系统的实现与仿真
　本文采用VHDL语言对系统进行描述，采用Altera公司的Stratix系列的EP1S10F484C5器件作为算法载体，通过QuartusII 5.0对系统进行综合、仿真并下载。根据S盒/逆S盒的内容生成内存初始化文件mif，用In-System Memory Content Editor工具对S盒的内容进行动态更新。仿真测试结果表明，相对于传统的设计，本设计消耗的资源大为减少。表1为本设计与传统设计在资源消耗和运行速度的比较。因为本设计在关键路径上添加了必要的选择控制单元，所以处理速度相对于传统设计有所降低。
　本文对AES算法进行了可配置设计，在数据分组长度固定的前提下，可以根据安全等级的需要选择不同分组长度的密钥进行加密运算。本文设计出1个统一的加解密硬件结构，使资源消耗大为减少。由于采用了3种长度规格的密钥，使得算法的安全级别灵活可变，用户可根据不同的安全需求灵活选择。在子密钥的生成上，本文采用可配置的方式来实现3种密钥生成算法，相对于使用不同的硬件结构实现每一种密钥生成算法，消耗的硬件资源进一步减少。算法中S盒的实现方式决定了其具备动态更新的特性，因此算法的安全性也得到进一步增强。综上所述，本设计非常适用于硬件资源受限且有多种安全级别需要的密码系统。

参考文献
[1]     National Institute of standard and technology, advanced  encryption standard[S]. FIPS197, 2001,11.
[2]     韦宝典，刘东苏，王新梅. 优化实现研究[J].计算机工程与应用,2002(20):4-6.
[3]     高娜娜，李占才，王沁.一种可重构体系结构用于高速实现DES、3DES和AES[J].电子学报,2006,34(8):1386-1390.
[4]     张清华.算法的高效实现及其性能分析[J].计算机应用，2004,24(2):12-14.
[5]     SHIM J H, KIM D W, KANG Y K,et al. A rijndael cryptoprocessor using shared on-the-fly key scheduler[C].  ASIC,2002. Proceedings.2002.IEEE  Asia  Pacific Conference,2002,89(92):6-8.
[6]     沈涵飞，甘 萌. 加密算法在低成本FPGA上的实现[J]. 计算机工程与应用，2004(22):116-119.