滞环电流控制是一种简单的Bang-Bang控制方案，易于实现，且具有很强的鲁棒性和快速响应能力，广泛应用于逆变电源[1]、有源滤波[2]、电机控制[3]、并网发电[4]等场合。但滞环电流控制的主要缺点是开关频率不固定。准确掌握开关频率的分布范围是进行电路(特别是滤波器)设计与优化、谐波分析、损耗计算的基础，具有重要研究意义。现有滞环电流控制频率分析方法[5-8]，忽略了一些非理想环节(如延时环节)的影响，同真实情况间存在较大误差。参考文献[5-8]等直接给出的仿真与实验结果，缺乏与频率理论计算的相互验证。本文将对逆变器滞环电流控制进行更准确的分析：首先分析考虑延时环节后滞环电流控制的详细物理过程；得出延时环节对实际电流改变量及瞬时开关频率的影响与表达式；与实验结果相验证。

1 考虑延时两态滞环电流控制分析
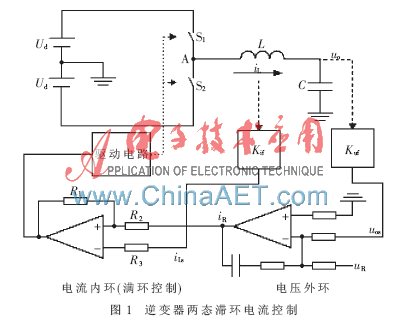
    在图1典型电路的基础上进行分析。Ud为输入电压，开关S1、S2构成半桥型桥臂,桥臂中点A输出的调制波经L、C滤波后得到正弦电压输出。采用电压外环电流内环（滞环）双环控制策略。
    图1中，电感电流iL经反馈电路后转变为电感电流反馈信号iLs，设反馈系数为Kif，则iLs=Kif iL；iLs与电流基准（电压环输出）iR相减得电流误差信号ie；ie再经滞环比较器得到PWM信号，驱动主电路功率管开关，控制电感电流在设定的正负环宽内。当ie大于正环宽时，滞环比较器输出低电平，逆变桥中点A输出-1态，电感电流下降；当ie低于负环宽时，滞环比较器输出高电平，逆变桥中点A输出+1态，电感电流上升，总保持ie在正负环宽内。

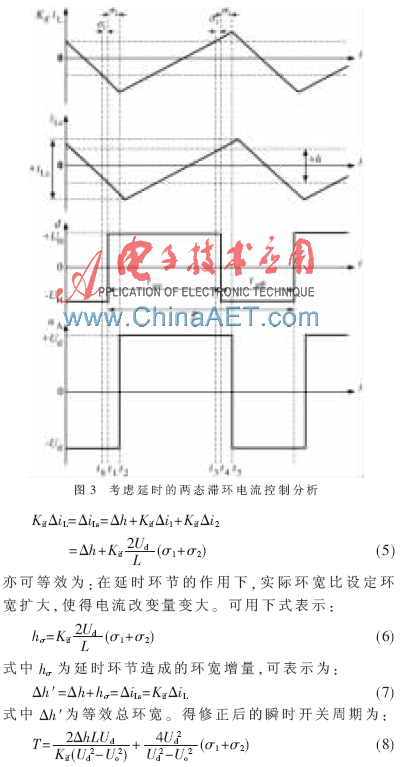
2 环宽、电流改变量的实验验证与分析
    由以上分析，可以得出以下一些推论：
    (1)由于实际系统延时环节的影响，实际电流改变量将大于设定的滞环环宽量值。
    (2)Δh取值较大时，延时环节的影响可以忽略不计；但当Δh取值较小时，延时环节在式(5)和式(6)中所占的比重很大，在两态滞环电流控制分析与设计中必须加以考虑。
    (3)环宽对电流改变量的控制是有限的，环宽减小到一定程度后，延时环节将起主要作用；电流改变量无法取很小的值，至少要大于Δi1＋Δi2。
    通过原理样机试验结果验证以上推论。主电路采用双buck逆变器[10]。该电路由两个buck直流变换器组合得到，各提供一半的电感电流，其详细原理不再赘述。样机参数如下：直流侧输入母线电压Ud=±180 V，输出单相110 V/400 Hz，反馈系数KiL＝0.333 Ω。电流采样使用LEM器件LA100-P，查阅其电气参数，采样延时σ1=50 ns。实测系统控制延时σ2=4 μs。滞环比较器电路如图1所示，环宽为：
    
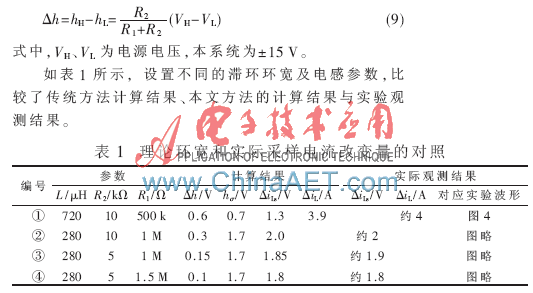
    这里需要先做如下说明：
    (1)环宽较大时，为维持输出电压波形质量，第①组使用电感值大于后三组。
    (2)表1对应实验波形如图4所示。图4(a)、图4(b)中，uo为逆变器输出电压，iL1为正半周电感电流，uA、uB分别为双buck逆变器两个桥臂中点输出的调制波形。iLS为电感电流反馈，有iLs=KiL ΔiL，由于反馈系数KiL量纲为Ω，电流反馈iLs已转变为电压信号，单位V；g2为双buck逆变器负半周开关管的驱动波形。
    (3)为了与图4实验波形保持一致，便于直观比较，第①组数据计算的是电感电流改变量ΔiL(（单位：A）；第②、③、④组数据计算的是电感电流反馈改变量ΔiLs，ΔiLs=KiL ΔiL（单位：V）。

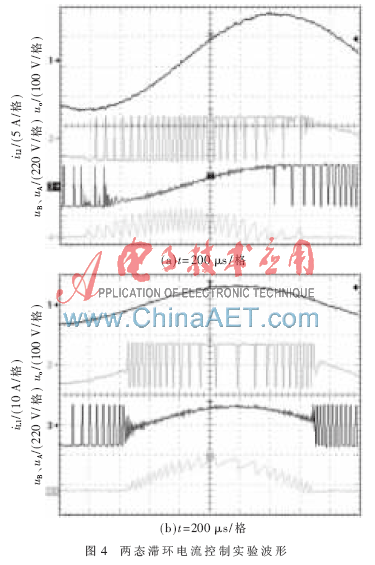
    (4)传统分析中，电流反馈改变量即为滞环环宽，表1中Δh亦表征传统方法计算结果。
      由表1、图4可验证前述推论：
      (1)实际电流改变量大于设定环宽，本文方法计算结果与实际观测结果基本吻合；传统分析电流改变量计算结果偏低，误差为hσ；
      (2)本样机的延时环节(主要是控制延时)造成的电流改变量大于设定环宽Δh的量值，其影响不能忽略不计；
      (3)由第②、③、④组数据，设定环宽值所占比重小，设定环宽值减小对电流改变量影响小，延时环节的影响起了主要作用。
3 开关频率计算与实验验证
    由于延时环节的影响，瞬时开关周期延长了，各次开关的瞬时开关频率及平均开关频率值均变低。而传统方法计算出的开关频率值必将高于实际值，且在延时环节比重较大时存在较大误差。

    本文就延时环节对两态滞环电流控制的影响进行了分析；推导出更吻合实际情形的瞬时开关周期表达式；能较为准确地分析出整个工频周期内各次开关频率。延时环节使得电感电流改变量大于滞环环宽（亦可等效为环宽扩大）。当延时时间折算环宽与设定环宽相当时，其影响不能忽略；当设定环宽减小到一定程度时，延时环节的影响将起主要作用。
    瞬时开关周期可分解为两部分，分别由设定环宽和延时环节引起，均与瞬时输出电压的平方相关。该表达式能更准确地反映实际情形。
参考文献
[1] MANSOUR M，ISLAM S M.A new vector -based hysteresis current control scheme for three-phase PWM voltage-source  inverters[J].IEEE Transactions on Power Electronics.2010，25(9)：2299-2309.
[2] ZABIHI S，ZARE F.A new adaptive hysteresis current control with unipolar PWM used in active power filters[J].Australian Journal of Electrical and Electronics Engineering.2008，4(1)：9-15.
[3] SRINIVAS P，PRASAD P V N.Voltage control and hysteresis current control of an 8/6 switched reluctance motor[C].Proceedings of the International Conference on Electrical Machines and Systems.Piscataway，NJ，2007.
[4] DALESSANDRO L，DROFENIK U，ROUND S D，et al. A  novel hysteresis current control for three-phase three-level PWM rectifiers[J].IEEE Applied Power Electronics Conference and Exposition-APEC，2005，Austin，1(1)：501-507.
[5] SRIKANTHAN S，MISHRA M K，RAO R K V.Improved  hysteresis current control of three-level inverter for distribution static compensator application[J].IET Power Electronics，2009，2(5)：517-526.
[6] GEORGE V，MISHRA M K.User-defined constant switching frequency current control strategy for a four-leg inverter[J]. IET Power Electronics，2009，2(4)：335-345.
[7] ALBANNA A Z，HATZIADONIU C J.Harmonic modeling of hysteresis inverters in frequency domain[J].IEEE Transacitons on Industrial Electronics，2009，25(5)：1110-1114.
[8] YAO Z L，XIAO L，YAN Y G.Dual-buck full-bridge  inverter with hysteresis current control[J].IEEE Transacitons on Industrial Electronics，2009，56(8)：3153-3160.
[9] 洪峰，刘军，严仰光.滞环电流控制型双buck逆变器[J].电工技术学报，2004，19(8)：73-77.
[10] 洪峰，嵇保健，杨伟，等.二极管钳位型双Buck三电平逆变器输入均压解耦控制[J].中国电机工程学报，
2012，32(9)：34-40.