文献标识码: A
文章编号: 0258-7998(2014)01-0090-03
由于激光陀螺具有高精度、可靠性好、性价比高、适合高动态环境等优点,广泛用于国防工业、航天航海及工业控制等领域中的导航、雷达与制导技术,成为目前惯导发展的主流方向。高速、高精度及高可靠性解调激光陀螺输出信号成为目前研究重点。
伴随着FPGA芯片门数、工作频率和数学运算能力的提升,尤其是其具有多任务和高速并行等特性优点,使得数字信号处理的FPGA得到普遍应用,使之成为激光陀螺高速解调的理想实现方案。
激光陀螺的输出信号中包含外界输入角速度、机械抖动角速度两部分信息,而机械抖动信号又叠加了伪随机噪声。针对激光陀螺解调的滤波器需衰减特别大、精度特别高及后续处理方便等,本文提出了基于浮点运算来设计滤波器,来满足信号滤波要求。
1 滤波器原理及参数分析
1.1 滤波器原理
常用数字滤波器有IIR和FIR两种滤波方式。由于FIR滤波器通带内输出相位延时是线性的,而IIR是非线性的,并且具有良好的线性相位和高稳定性,在数字信号处理领域中应用广泛,因此采用FIR滤波结构设计[1]。其输入输出函数如下:
1.2 滤波器参数设计
利用MATLAB中滤波器设计工具来设计满足要求的FIR滤波器,在命令界面输入FDATOOL打开滤波器设计环境[2]。
由于外界输入陀螺角速率频率在0~20 Hz,而需要滤掉的陀螺信号中的机械抖动信号和随机噪声分别达到300 Hz左右和1 kHz以上。因此设计FIR低通滤波器,规定截止频率为100 Hz,采样频率为10 kHz。得到滤波系数。
将滤波系数的值a存入到FPGA内部的ROM中,而FPGA内部ROM初始化数据只支持整型二进制、十进制和十六进制三种数据类型,因此需要把浮点数a表示为其机器码。由于FPGA中采用的是单精度浮点算法,而MATLAB中生成的滤波系数是双精度浮点格式,因此还需要将双精度浮点转换为单精度浮点格式。在MATLAB中输入如下命令得到a的十六进制单精度机器码b:
>> b=single(a);
>> format hex
>> b
将b的值保存到后缀为.COE的文件中,用此文件来初始化FPGA内部RAM,并配置成只读模式(ROM),得到FIR滤波器的系数ROM。
2 滤波器的FPGA实现
滤波系数定点化就是对滤波系数乘以一个较大的系数然后取整,用整数来近似替代浮点小数。滤波器的卷积过程也变成了定点运算,滤波结束后对滤波结果除以所乘系数值便可得到近似的滤波结果[3]。这种方法使得滤波器设计简单、易于实现。但由于激光陀螺数据处理是一个对精度要求很高的领域,要达到这种高精度指标,需要把系数整形化倍数提高到226以上,这种误差的引入对滤波精度有很大影响。若采用浮点运算,滤波系数也就采用浮点表示,不会因为整形化带来误差,输入输出范围较大,输出也是标准的计算机数据格式。但由于FPGA内部浮点运算需自己建立运算模块,实现起来复杂,一般只用在高精度宽量程领域。
2.1 浮点数据格式
目前计算机中常用的浮点格式是IEEE的单精度32位浮点表示方式以及64位的双精度浮点表示方式。在FPGA和DSP中,最常用的是32位的浮点表示方式。IEEE 754单精度浮点数可表示为如图2所示格式,其中符号位s一位,阶码e占8位,为无符号数,但是e带有127的偏移量,因此小数点的移动位数为e-127,尾数f占23位,为定点部分数值,但隐藏了1,位数表示值为1.f。
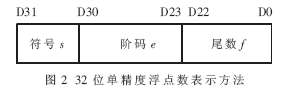
按照IEEE 浮点数计算标准[4],浮点数X=(-1)S×2e-127×1.f。本模块中采用IEEE 32位单精度浮点格式,因此对于IEEE中扩展40位单精度和64位双精度格式就不再进行讨论。
2.2 浮点加法模块设计
浮点数的加减运算过程较为复杂,需要对加法的两操作数进行对阶、尾数运算、结果规格化及舍入处理等。为了减少在加、减法器设计时的工作量,采用XILINX自带的浮点加减运算IP核,通过较简单的配置,便可以得到可用的浮点数加、减模块。在FPGA程序设计时,可以通过交换操作数的方法来避开浮点的减法运算,因此只需生成浮点数加法模块,生成的模块例化图如图3所示。在ISE中对该模块进行仿真,同样采用50 MHz的主时钟,仿真波形图如图4所示。


对该浮点乘法模块进行仿真,以验证乘法器的功能。由于XILINX仿真器中不能直接计算二进制数对应的浮点数大小,为了减少验证时手动的计算量,采用与表1一样的输入数据,仿真波形如图6所示。

从仿真结果中可得,三组输入数据对应的输出分别为:C6F50A00、C1360000、BD360000,对应的十进制数分别为:-31 365、-11.375、-0.032 714 843 75,对照表1可知计算结果正确,设计的浮点乘法器能够精确进行浮点数的乘法运算,乘法周期大概为8个时钟周期,模块在50 MHz时钟下工作正常。
2.4 滤波器系统设计
基于以上设计的浮点加法器和浮点乘法器,在FPGA中实现FIR滤波器。系统顶层原理图如图7所示。
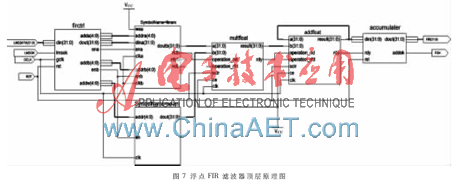
系统控制逻辑控制firctrl模块从wrom模块中读取浮点滤波系数、陀螺输出计数值写入firram模块、计数值读出firram以及浮点乘法模块multfloat的运算,使得几个模块能在一定时序下稳定工作,firram模块和firctrl模块的配合实现了计数值的存储及移位功能;浮点乘法器模块还包括两个18位×18位的乘法器的组合,通过乘法分解,实现了高位宽32位×32位乘法运算;累加器模块addfloat负责将浮点乘法器输出值进行累加并取位。整个系统完成了FIR滤波结构计数值和滤波系数的卷积过程。
3 实验测试
3.1陀螺静态实验
在静态(只有地球自转)的情况下,利用本滤波器对机械抖动激光陀螺的输出解调性能进行测试,在上位机中以1 s为单位进行数据分析和波形绘制,上位机测试界面截图如图8所示。
从图8中可以看出,静态时对激光陀螺信号解调结果值波动较小,10 S平均值为5.202 8。10 S方差为0.011 0,100 S方差为0.003 1。300 S方差为0.001,本滤波器能很好地完成激光陀螺输出信号的解调,并且具有很高的精度和稳定性。
3.2 陀螺动态实验
为了验证专用滤波器的动态性能,需要在外界不同输入角速率的情况下对进行测试。将激光陀螺放置在标准转台上,让转台处于不同转速下。测试过程中,转台会在每转动360°时对其外输出一个定角脉冲,脉冲宽度为2 μs左右,让滤波结果在定角脉冲没有到来时一直累加,当定角脉冲到来时向外发送一次数据,同时将累加器清零。在去除地球自转影响后,测试结果如表2所示。

由表2测试数据中可以看出,在不同角速率的情况下,转台转动360°激光陀螺的输出值相等,由此可见本专用滤波器同时具有很高的精度和具有很大的动态处理范围,能很好地完成对陀螺输出数据的精确解调。
通过软件仿真、静态测试和动态测试,得到一系列测试数据。对这些数据进行分析,本滤波器具有很高的滤波精度和很宽的动态响应范围。基于以上实验及数据结果可知, 利用FPGA实现的浮点滤波算法,能满足对激光陀螺信号精度和响应速度具有苛刻要求的应用场合。
参考文献
[1] U.Meyer-Baese著.数字信号处理的FPGA实现[M].刘凌,译. 北京:清华大学出版社,2011.
[2] 王宏. MATLAB 6.5及其在信号处理中的应用[M].北京:清华大学出版社,2004:220-251.
[3] 任晨纲.基于FPGA的激光陀螺捷联惯导系统信号的检测与处理[D]. 长沙:国防科技大学,2009.
[4] 吕妍红,崔中兴.环形激光陀螺信号分析与处理[J].传感技术学报,2004(6).
[5] 崔云娟.基于FPGA的浮点运算器的设计及在雷达中的运用[D]. 西安:西安电子科技大学,2007.


