摘  要： 为识别同频音频广播节目，提出在节目源间歇地添加确知的微弱正弦周期信号作为识别信息，Duffing振荡器阵列检测解调的音频信号中弱正弦周期信号并确定时隙内Duffing振子运动状态的跃变次数，以识别音频广播节目。使用16个音频进行仿真，从仿真结果可以看出，Duffing振荡器阵列检测到的李雅普诺夫指数值跃变次数与间歇加入的微弱正弦周期信号的次数一致；信噪比在46 dB～52 dB之间，符合音频广播的信噪比要求，该识别方法可行。
关键词： Duffing振荡器阵列；弱信号检测；音频广播节目；李雅普诺夫指数

    广播安全播音中，节目监测是一个重要环节。现有的同频音频广播监测采用切断相关的节目源方法，不能自动监测；而数字水印方法实验中音质严重下降，不适于音频广播。
    Duffing振荡器具有检测微弱周期信号的功能[1]。音频信号是一个随机数[2]，与微弱正弦周期信号有很大的差异，它们对处于临界状态的Duffing系统有不同的影响。此外，轨道跟踪法计算李雅普诺夫指数受噪声影响大[3]。因此，提出在音频广播节目源间歇地添加确知的微弱正弦周期信号作为识别信息，使用不同阈值的Duffing振荡器阵列对确知弱正弦波信号进行检测并确定时隙内Duffing振子运动状态的翻转次数，实现同频音频广播节目的识别。


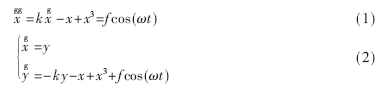
    Duffing振荡器弱信号检测：在驱动力f从小到大变化中得到阈值fc，它是系统从混沌运动到长周期运动跃变时驱动力临界值。处于临界状态的Duffing系统，对输入到系统的周期信号非常敏感，即使幅度很小的周期信号也能使系统的相图发生跃变。因此，Duffing振荡器运动状态是否跃变可判断输入信号是否存在微弱的周期信号。图1是系统的两种状态。

2 间歇地添加弱正弦信号的音频广播节目识别
    为监测发射机播音情况，对不同发射机的信号源间歇地添加不同频率的微弱正弦信号，接收端解调出带有微弱周期信息的音频信号，振荡器阵列检测时隙内添加识别信息的次数。
    (1)识别信号的添加
    正弦波发生器产生微弱的单频正弦信号，通过开关电路形成间歇的微弱正弦波信号，控制开关频率以产生时隙内正弦波的次数，如图2所示。

    (2)信号的解调
    获取微弱正弦波的识别信息，需将调制信号解调，解调的信号中将含有大幅度的音频信号和微弱的正弦周期信号，如图3的虚线框部分。
    (3)Duffing振荡器阵列检测
    Duffing振荡器检测系统用于判定Duffing系统处于混沌运动状态还是周期运动状态。Duffing系统的状态可通过观察相图来确定，它是人工行为，效率低且不适于工程应用；李雅普诺夫指数(Lyapunov exponent)定量描述了混沌振荡器的这种现象的量[3-4]。在诊断和描述混沌信号时，李雅普诺夫指数是一个不变量，它的正负性用来判定系统是否混沌。
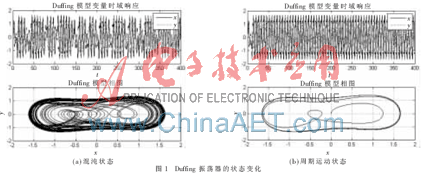
    对于Duffing振子，若其Lyapunov指数均小于0，系统处于周期运动状态；若存在一个Lyapunov指数大于0，则系统处于混沌运动状态。同时实验中发现，用改进C-C方法[5]计算时间序列的嵌入维数m值为无穷大（Inf）时，观察到Duffing振子的相图都为混沌运动状态。因此，当计算时间序列嵌入维数m的值为无穷大时，相应的Lyapunov指数以‘0’代替，表1和表2中以‘/’表示。微弱信号以[0，0.01]形式间歇加入，两次计算Lyapunov指数值，Lyapunov指数?姿1值从正数或0跃变到负数，说明Duffing振子运动状态从混沌状态跃变到长周期运动状态，计数器加1。由计数器的值指示时隙内加入微弱正弦波的次数。不同类型的音频信号需要不同阈值的Duffing振荡器，两个阈值的Duffing振荡器检测阵列如图4所示。

    (4)判决
    固定时隙内，各发射机信号源加入的弱周期信号的频率和次数不同，据Duffing振荡器阵列检测到的李雅普诺夫指数值跃变次数，可识别播出音频节目的发射机。
3 材料和实验
    (1)实验材料
    实验中，使用16个音频片段（9个语音，7个音乐），格式为wav，幅值在[-1，1]之间。
    (2)仿真实验
    ①一个频率音频节目用一部发射机播出情况
    设系统频率为ω=1，输入s(t)=acos(ωt)+2z(1：length(t))，ψ等于系统固有频率，z是音频片段信号。a=[0，0.01，0，0.01，…]是时隙内加入的10次正弦信号。振荡器阵列检测到Lyapunov指数值从正数或0跃变到负数的次数也是10次。输入信号幅值、计算的相空间嵌入维数m和时间延迟tau、最大李雅普诺夫指数值1和振荡器运动状态翻转次数如表1所示。

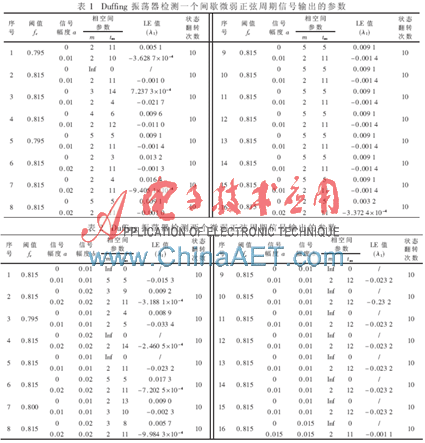
    ②一个频率音频节目同时用两部发射机播出情况
    设Duffing系统频率为ω=1，输入s(t)=acos(ωt)+bcos(3ωt)+4z(1：length(t))，即一部发射机节目源加入微弱周期信号的频率为ω，与Duffing系统固有频率相同，另一部发射机节目源加入微弱周期信号的频率为3ω。输入信号幅值、计算的重建相空间的嵌入维数m和时间延迟tau、最大李雅普诺夫指数值?姿1和Duffing振荡器运动状态翻转次数如表2所示。
    (3)信噪比分析
    实验的第一种情况采用2倍的音频信号幅值，第二种情况采用4倍的音频信号幅值。由信噪比定义SNR=20log，大多数音频片段的信噪比在46 dB～52 dB之间。
    从仿真结果和分析可以看出，Duffing振荡器阵列对带有微弱正弦周期信号的音频节目的检测，能输出稳定的李雅普诺夫指数值，在时隙内检测到的李雅普诺夫指数值跃变次数与间歇加入的微弱正弦周期信号的次数一致，实现了音频节目的识别。信噪比在46 dB～52 dB之间，符合音频广播节目信噪比的要求；识别信息加入方法简单。该同频音频节目识别方法可行。
参考文献
[1] Liu Ding，Ren Haipeng，Song Li，et al.Weak signal detection  based on chaotic oscillator[J].IEEE，2005(3)：2054-2058.
[2] 高晋占.微弱信号检测(第2版)[M].北京：清华大学出版社，2011.
[3] 杨邵清，章新华，赵长安.一种最大李雅普诺夫指数估计的稳健算法[J].物理学报，2000，49(4)：636-640.
[4] WOLF A，SWIFT J B，SWINNEY H L，et al.Determing Lyapunov exponents from a time series[J].Physica 16D，1985：285-317.
[5] 秦奕青，蔡卫东，杨炳儒.非线性时间序列的相空间重构技术研究[J].系统仿真学报，2008，20(11)：2969-2973.