文献标识码: A
文章编号: 0258-7998(2014)07-0058-03
随着网络的开放、共享及互联程度的不断扩大,网购逐渐渗透到人们的日常生活中,给人们带来了便利,同时也使个人的隐私安全受到威胁。快递员素质良莠不齐,快递员倒卖快递单号泄露客户个人信息的新闻屡见不鲜。因此,如何在快递员速递包裹的这一环节中保护消费者个人隐私安全是本文的主要研究内容。
密码技术[1]作为信息安全的核心技术,主要由密码编码和密码分析组成。Diffie与Hellman在1976年发表论文“New Direction in Cryptography”,提出公开秘钥密码技术思想,至1977年,第一个比较完善的RSA加密算法由Rivest、Shamir和Adleman提出。此后,研究人员提出了ElGamal公钥密码技术、椭圆曲线(ECC)[2]公钥密码技术等。至今,RSA公钥加密算法仍是最易理解和实现的一种算法,不仅可以用于加密,也可用于数字签名。RSA算法的安全性主要依赖大数分解的难度。依现在的技术,1 280 bit的密钥在未来15年内是安全的[3],1 024 bit的密钥对于除了保存极为重要的数据之外在抗攻击上也是可以接受的。不过RSA作为非对称加密技术,相对于对称加密术而言,运算速度比较慢。对于快递这一每天处理大量数据且非常重视效率的行业来说,加密解密速度慢会对企业和客户造成不便,因此寻找一种既快捷又安全的加密方式显得尤为重要。1982年,Quisquate和Couvreur提出了一种RSA的变型算法,称为RSA-CRT[4-5]算法,这是一种基于中国剩余定理的能够加速RSA解密的算法。1990年,Wiener提出了另外一种RSA的变型算法,称为重新平衡-RSA[6],进一步通过把解密成本转移到加密成本上来加速RSA解密。文中提出了一种基于重新平衡-RSA的变型算法,它的公开指数e比模量更小,从而能够在保持较低解密成本的同时有效地减少加密成本。可见其在保证信息安全的同时也提升了速度,因而十分适合应用于快递信息的加密解密。
1 速递中存在的两个安全隐患
图1为简略的快递过程。其中造成客户隐私泄露的环节包括两个方面:第一,快递公司将贴有快递单的货物分发到快递公司各地配送中心的过程中,工作人员都可以通过快递单号在内网查询到客户的详细信息,此环节中若没有严格的权限限制,易造成客户隐私泄露;第二,各中心快递员将货物派送到收货人的环节中,快递员能第一手获得客户信息,而各快递公司所聘快递员素质良莠不齐,也易造成客户信息的泄露。因此希望任何环节中的工作人员获得的消费者信息越少越好。
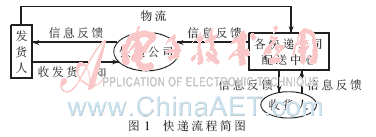
本文将主要解决第二个环节可能带来的隐私泄露,即在快递员速递包裹的这一环节中保护消费者个人隐私安全。
这里不考虑快递员送包裹时使用快递单的形式,而是设想将快递员当天需要送出包裹的客户的个人信息储存在Android系统的手机中并加密,加密内容包括客户的名字、手机号和物品内容等。为了让快递员获得的信息最少,可以用家庭住址作为加密文件的文件名。客户用快递公司事先发给客户的一串号码(解密密钥)解密,然后核对自己的信息,确认无误后,按确认按钮将数据返回到快递中心,保证是客户本人操作。这样即使在手机没有信号的时候,快递员因为没有解密密钥也无法冒充客户收货。因此,找到一种既能安全加密/解密速度又快的算法很重要。人们基于RSA算法开发了大量的加密方案与产品。Jdk1.5中提供了对RSA算法的支持[7],所以可以在Java为支撑的安卓系统中实现RSA算法[8]。
2 一种基于RSA的新的加密算法
这里介绍一种基于重新平衡-RSA密钥的生成算法,其公开指数比要小得多。公钥指数e的取值范围N1/2<e<N。密钥生成算法是基于以下来自数论的基本定理的。
2.1 传统重新平衡-RSA加密算法
为了进一步提高解密速度,Wiener提出了一种通过转换一些加密/解密需要做的工作的变型RSA-CRT(RSA-中国剩余定理)算法,称为重新平衡-RSA[9]。其加密解密步骤与RSA-CRT[10]一样。模数为n位,CRT指数为nd位,具体加密步骤如下:

上述算法中公钥是一对(e,N),私钥为元组(dp,dq,p,q)。如果按φ(N)的大小排序,e大致一样的可能性很高。为了相对于比RSA-CRT进一步减少解密时间,则会导致加密时间几乎最大化。
定理1 a和b是两个互质的整数且不等于1(gcd(a,b)=1且a,b≠1)。对每一个整数,存在一个唯一的有效可计算的一对整数(uh,vh)满足auh-bvh=1,其中(h-1)b<uh<hb且(h-1)a<vh<ha。
定理2 三元线性模块化方程f(x,y,z)是具有整数系数的线性多项式。对任意ε>0,存在正数M0,当任意整数M>M0且两个数互质时,至少存在一个非恒定的系数f,使得3个线性独立的多项式f(x,y,z) (mod M)的每个根(x0,y0,z0)同时也是3个多项式对M取模的一个根。若|x0|<X,|y0|<Y,|z0|<Z且XYZ<M1-ε,则对于一些X,Y,Z的边界值,(x0,y0,z0)仍然是3个多项式中每个多项式的一个根。如果这3个多项式代数独立,则可以计算出(x0,y0,z0)。
2.2 变型重新平衡-RSA算法
以(n,ne,nd)为输入,ne>n/2,输出一个有效的公钥(e,N),对应的密钥为(dp,dq,p,q),其中|N|=n,|e|=ne且|dp|=|dq|=nd。
输入:(n,ne,nd),ne>n/2
(1)e←随机的(ne)位奇数;
(2)kp1←随机的(nd)位整数使得gcd(kp1,e)=1;
(3)使用定理2(h=2),计算(dp,P)使之满足edp=kp1 P+1,其中kp1<dp<2 kp1,e<Q<2e;
(4)P=kp2(p-1),kp2是一个(ne-n/2)位的整数,p是一个素数,如果等式不成立则返回到第(2)步;
(5)kq1←随机(nd)位;
(6)整数gcd(kq1,e)=1;
(7)使用定理2(h=2),计算(dq,P)使之满足edq=kq1 Q+1,其中kq1<dq<2kq1,e<Q<2e;
(8)Q=kq2(q-1),kq2是一个(ne-n/2)位的整数,q是一个素数,如果等式不成立,则返回到第(5)步。
输出:公钥(e,N),私钥(dp,dq,p,q)。
从上面的算法可以看出,它主要是由步骤(2)~(4)和步骤(5)~(7)构成的。因此,每个循环中的迭代次数是预期的,使得算法复杂度是线性的。通过实验观察到,在n=1 024时,每个循环迭代的次数大约为215。在每一个循环中,试图将一个ne位的整数(P或Q)分解成两个数,(ne-n/2)位与n/2位,若想成功分解,则需要使用椭圆曲线法(ECM),比如,不能使(ne-n/2)太大,因为ECM的复杂度是基于小因子的比特长度。因此,必须严格选择ne,使它尽量接近n/2,比如,至少使(ne-n/2)<80,因为要考虑到现在的计算机成功分解ne的能力。
2.3 不同RSA变型算法的比较
从表1中可以看到,当明文m=80、模为1 024位时,从加密解密两个方面,将新的变型算法与其他几个RSA算法做了一些参数比较。新算法中使用2k+1作为加密指数的形式,例如,当(ne,nd)=(592,190)时,与传统的重新平衡-RSA相比,加密速度提高了2.6倍,解密速度降低了20%。

本文介绍了一种基于重新平衡-RSA的变型算法,可以自行选择加密指数和CRT-指数。由表1可以看到,新算法的加密解密消耗比例分别为4.17与0.634。对于保护快递中的个人隐私而言,用户在解密时不希望花费太多时间,这个比例适合应用于快递中心与客户二者之间。当然在保证一定安全的情况下,进一步缩短加密解密时间是下一步需要研究的问题。
参考文献
[1] Yin Xucheng,Wu Keke,Li Huiyun.A randomized binary modular exponentiation based RSA algorithm against the comparative power analysis[C].In:Proceedings of 2012 IEEE International Conference on Intelligent Control,Automatic Detection and High-End Equipment(ICADE 2012),2012:160-165.
[2] 徐茂智, 游林.信息安全与密码学[M].北京:清华大学出社,2007.
[3] JOCHEMZ E,MAY A.A polynomial time attack on RSA with private CRT-exponents smaller than N0.073[C].In:Proceeding of Crypto 2007,LNCS 4622,Berlin:Springer-Verlag,2007:395-411.
[4] 王保仓,韦永壮,胡予濮.基于中国剩余定理的快速公钥加密算法[J].西安电子科技大学学报(自然科学版),2008,35(3):449-454.
[5] 刘承斌,耿也,舒奎,等.有关中国剩余定理在多个素数的RSA解密运算中的加速公式的论证以及加速效率的估算[J].大连工业大学学报,2012,31(5):372-375.
[6] Sun Hungmin,Wu Muen,HINEK M J,et al.Trading decryption for speeding encryption in Rebalanced-RSA[J].The Journal of Systems and Software 82,2009,82(9):1503-1512.
[7] 赵军.基于Android平台加密算法的研究与实现[D].南京:南京理工大学,2012.
[8] 司光东,杨加喜,谭示崇,等.RSA算法中的代数结构[J].电子学报,2011,39(1):242-246.
[9] Liu Qing,Li Yunfei,Li Tong,et al.The research of the batch RSA decryption performance[J].Journal of Computation Information Systems,2011,7(3):948-955.
[10] Sun Jin,Hu Yupu.Identity-based broadcast encryption scheme using the new techniques for dual system encryption[J].Journal of Electronics & Information Technology,2011,33(5):1266-1270.

