在数据采集系统中，为了防止传感器输出的模拟信号在采集之后发生混叠失真，需要在调理电路中实现模拟信号抗混叠滤波器。滤波可以有效地滤除干扰信号,消除噪声信号。如果需要抑制的信号和需要通过的信号在频率上非常接近，则普通的低阶(一阶、二阶)有源滤波器的截止特性可能就不够陡峭，需要采用高阶滤波器^[1]。

        传统的高阶连续时间模拟滤波器电路本身含有大体积的电容以及RC元件，对频率特性在精度和稳定度方面有严格要求，无法制造成单片结构^[2]。因此在现代集成电路工艺中，高阶连续时间模拟滤波器很难得到精确的电阻值和电容值，而且电阻值随温度变化很大，精度只能达到30％^[3]。

1 开关电源滤波器电路分析

        开关电源滤波器由受时钟脉冲信号控制的模拟开关、电容和运算放大器三部分组成。这种滤波器以数据采样技术代替大电阻，减小了芯片的面积和功耗，电路的特性与电容器的精度无关，仅与各电容器电容量之比的精确性有关。在集成电路制作中通过准确控制每个电容电极的面积，能够获得高精度的模拟集成滤波器。

1.1 开关电容单元

        图1所示电路是基本开关电容单元。其中电容器一般使用MOS电容，模拟开关采用栅极受时钟信号Ф控制的MOS管实现。当Ф为高电平时，开关K1闭合，K2打开，电源为电容C充电，电荷转移到电容器C上；当Ф为低电平时，开关K1打开，K2闭合，电容器放电。如果按照频率f_CLK交替地将两个开关打开、闭合^[4]，则电荷按速率i移动，即：

        由式(1)可以看出信号在一个采样周期结束时才被采样一次，因此对于采样系统而言，这个电流不是连续的电荷运动。式(1)进行变换可得：

其中，T_CLK为采样周期。可将该比值定义为电路的等效电阻R_eq。从原理图中可以看出电路正常工作的条件是开关交替切换，即必须确保两个开关不能同时闭合，并且在一个开关闭合之前另一个开关能够及时打开。此外必须合理选择开关的切换频率，以确保有足够的时间完成充放电，即开关切换频率要远大于输入电压U_i的频率。

        开关电容滤波器电路原理图及输出电压波形图如图2所示。

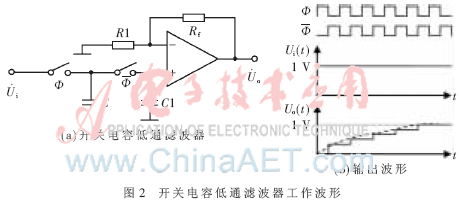
        由式(2)可以看出，等效电阻与电容成反比，与开关切换频率也成反比。在集成方案中，滤波器中集成的电容值是固定的，滤波特性受开关频率的控制。电路的通带截止频率fp决定于时间常数：

        由于f_CLK是时钟脉冲，频率相当稳定；而且C/C1是两个电容的电容量之比，在集成电容制作时易于做到准确和稳定，所以开关电容滤波器具有稳定的截止频率。

1.2 开关电容滤波器混叠效应理论分析

        LTC1569是Linear公司一种具有采样特性的十阶开关电容低通滤波芯片，它可以不需要外部时钟，通过一个外部配置电阻对截止频率进行编程设置，精度可达3.5%。配置电阻对芯片内部晶振振荡频率进行1、4或16分频。当引脚6（Rx）与引脚7（V₊）之间接一个配置电阻R_CLK就可以启动内部时钟。配置电阻与截止频率的对应关系式为：

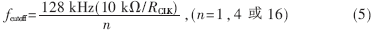
        当5引脚（DIV/CLK）短接到4引脚（V_-）时，内部分频设置为1:1；当5引脚通过100 pF电容接4引脚时，分频设置为1:4；当5引脚短接到7引脚时，内部分频设置为1:16。

        后置低通滤波器作用是消除开关电容滤波器对模拟信号采样时产生的混叠噪声。LTC1569滤波采样频率满足^[5]：

        由参考文献[5]知，后置滤波器的截止频率f_L需要满足：

其中，f_SCF为开关电容滤波器的截止频率。且：

其中，K_L为二阶低通滤波器10倍频程理想衰减系数，A_L为二阶低通滤波器实际衰减系数。考虑到LTC1569滤波器输出的高频噪声实际水平，二阶滤波实际衰减率约为0.7。

      根据式(7)和式(8)可得：

2 开关电容滤波器仿真

        FilterCAD是Linear Technology公司为开关电容集成电路和有源RC集成电路设计的专用仿真软件。用户可以方便地设计包括Butterworth、Bessel、Chebyshev、elliptic、最小Q值Ellipic响应和用户自定义响应在内的低通、高通、低通和带阻开关电容滤波器。通过电路分析可以掌握滤波器的传输函数、频域、时域响应，从而更好地了解设计结果。根据设计要求，变换器在0～5 kHz范围内幅度无衰减，因此设定截止频率为7 kHz。仿真电路及幅频特性曲线如图3所示。

        由图3(b)所示仿真结果看以看出，在截止频率7 kHz处，增益衰减-3 dB；在70 kHz频率处，衰减达到-100.72 dB。

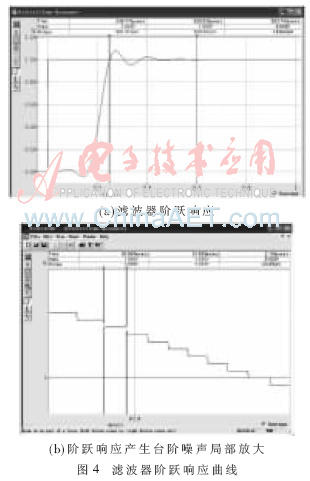
        滤波器阶跃响应曲线如图4所示。开关电容对模拟输入信号的采样将时间连续信号转换成时间离散信号。因此开关电容滤波器输出一连串阶梯状的噪声信号，在时域上不连续，而且在频域上增加了新的高频成分。所以对于开关电容滤波器电路，还需要额外考虑混叠问题。但由于滤波器的采样速率非常高，通常是几十倍的过采样，所以只需要在开关电容滤波器后再加入一个低阶的低通滤波电路抑制高频噪声。仿真结果显示，台阶噪声频率约为500 kHz。

3 实验结果

        本文选用二阶压控低通滤波器作为开关电容滤波器后续的滤波电路。二阶压控有源低通滤波器在通道内信号能量没有损耗，还可以实现放大，负载效应不明显，结构简单，成本低廉。考虑到变换器输出频率响应要求精确到5 kHz，并且由于电路中电阻、电容容差的影响，十阶低通滤波器的编程电阻R1*选为42.2 kΩ（1%），截止频率为7.58 kHz。滤波电路原理图如图5所示。

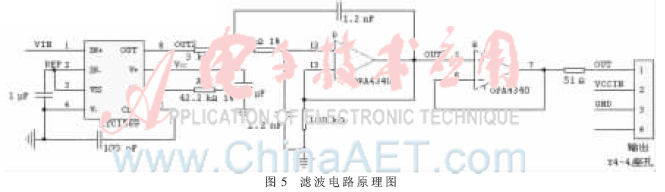
        由上述混叠效应理论分析可知，十阶低通滤波器LTC1569输出的高频台阶噪声频率f_NS=2·f_CLK±f_SCF=2×32×f_SCF±f_SCF=492.7 kHz，与图4所示仿真阶梯噪声频率基本一致。

        根据式(9)计算，电路中二阶低通滤波器截止频率应小于48.512 kHz，电路实际采用截止频率为44.2 kHz、增益为1.24倍的二阶压控有源低通滤波器作为开关电容滤波的后置滤波电路。实测变换器电路各个节点电压输出波形如图6所示。

        由实验波形图可以看出，当输入6 kHz模拟信号时，经过十阶低通滤波器LTC1569输出波形出现了频率约为500 kHz的阶梯噪声，经过二阶压控低通滤波器对阶梯噪声进行抑制后，滤波效果良好。滤波电路频率特性曲线如图7所示。

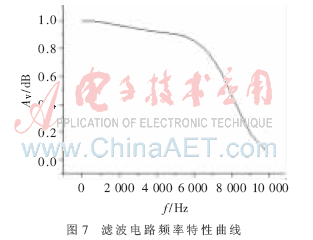
        针对开关电容滤波器的采样特性，需要在其后面接后续低通滤波电路。本文通过对采样频率的理论分析及仿真实验，定量地分析了后续所需低通滤波电路的截止频率，并通过实验验证了该滤波电路能够解决开关电容滤波电路出现的混叠现象。

参考文献

[1] 惠鹏飞，姚仲敏，夏颖，等.基于FPGA的无线传感网络信道波形整形滤波器[J].电子技术应用，2013，39（7）：35-37.

[2] 赛尔吉欧·佛朗哥.基于运算放大器和模拟集成电路的电路设计（第三版）[M].西安：西安交通大学出版社，2009.

[3] 常杰，刘诗斌.开关电容低通滤波器的设计[J].电子设计工程，2012，20(8)：171-173.

[4] 高燕梅，王丽，付圆媛.开关电容滤波器设计与仿真方法的研究[J].吉林大学学报（信息科学版），2005，23(4)：373-377.

[5] 赵天成，赵英俊.开关电容滤波器前置、后置滤波器的设计[J].电子设计工程，2011，19(12)：143-146.