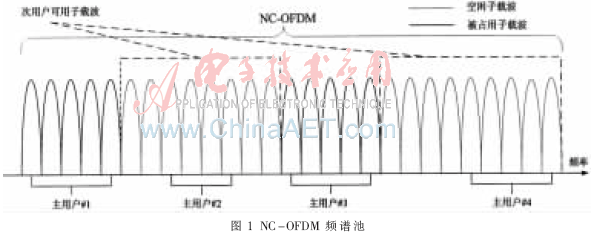
非连续正交频分复用(NC-OFDM)技术是一种比较容易实现的动态频谱传输技术^[1]，它被认为是4G移动通信中最具竞争力的一个候选传输技术。NC-OFDM频谱池如图1所示，其中信道的空闲状态和被占用状态是随机出现的。由图可看出NC-OFDM技术可将非连续的频谱碎片聚合起来，提高了频谱利用率。

        导频辅助信道估计^[2]是NC-OFDM系统的关键技术之一。由参考文献[3]知，当子载波连续分布时，等间隔、等功率的导频是最优的。然而在NC-OFDM系统中可用频段是非连续的和动态变化的,如果使用等间隔导频设计，某些导频就可能位于主用户的频段内，干扰主用户的正常通信。因此对于NC-OFDM系统需要寻找新的导频设计方法。参考文献[4]提出了一种适用于NC-OFDM系统的次优导频设计方法，通过优化归一化信道均方误差设计NC-OFDM系统的导频位置。这种方法虽然具有良好的性能，但是随着子载波数量的增加，设计过程会变得越来越复杂。参考文献[5]推导出了信道MSE的上限公式，通过优化MSE上限设计导频位置。这种设计方法简化了设计复杂度，但是可能造成各个活动频段内分配的导频数与频段宽度不成比例，从而影响信道MSE和BER性能。

        在参考文献[6]的基础上，研究了NC-OFDM系统的导频设计，使之转化为一类确定性的数学模型，并提出了求解该问题的离散粒子群算法。这种方法不仅具有良好的性能，并且复杂度较低，程序通用性较高。当NC-OFDM系统参数改变时，只需改变程序中活动子载波序列和总的子载波数等系统参数，其他部分都保持不变。

1系统模型

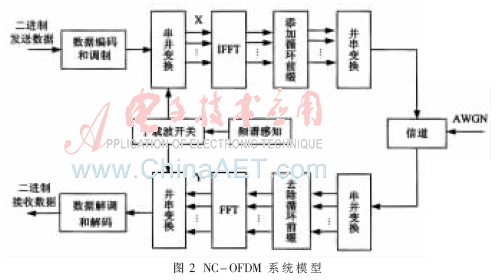
        NC-OFDM系统模型^[7]如图2所示。第k个活动子载波上的接收数据可以表示为：

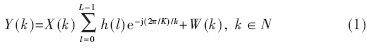
其中X(k)是发送数据，K是总的子载波数，N是活动子载波序列；W(k)是均值为0方差为σ_w²的加性高斯白噪声； h=[h(0)…h(L-1)]^T为信道的冲激响应，L是信道路径个数。

2 信道MSE

        设有P个导频信号，P={p₀…p_P-1}表示导频位置的集合。由式(1)知，接收到的导频信号为：      

这里，视各个导频子载波是等功率的，φ表示导频平均功率。

3 问题描述及数学模型

        NC-OFDM系统的导频设计可描述为： C={h₀,h₁…h_N-1}为活动子载波的集合，N为活动子载波总数。x_j=1和x_j=0分别表示第j个活动子载波被选作导频和不被选作导频。x=[x₀,x₁…x_N-1]是一个N维变量，由x可以确定F_P。现在问题是：从N个活动子载波中选择P个子载波作导频，使信道MSE最小。其数学模型如下：

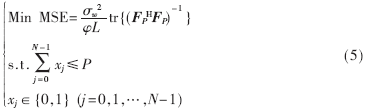
4 NC-OFDM系统导频设计的离散粒子群算法

        0-1背包问题的数学模型如下所示：

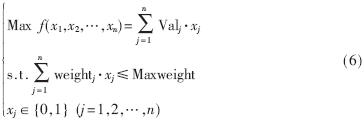
        由式(5)和式(6)可看出，NC-OFDM系统导频设计的数学模型和0-1背包问题的相似，因此可将解决0-1背包问题的离散粒子群算法改进后，应用到NC-OFDM系统中解决导频设计问题。

        具体步骤^[8]如下：

        (1)确定参数值

        确定种群规模M,最大迭代次数Maxiter，学习因子c₁和c₂，并令进化代数k=0。

        (2)初始化所有粒子的位置和速度

        粒子位置：

其中v_max和v_min表示速度的最大最小限制值。

        (3)计算粒子的适应值并更新记忆库

        根据式(4)计算粒子的适应值，并更新PB_i^k和GB^k。其中PB_i^k为第i个粒子进化k代所经历的最好位置，GB^k为整个种群进化k代所经历的最好位置。

        (4)更新粒子的速度和位置

        为了更新粒子的速度和位置，首先引入Sig函数

        需注意的是：对粒子位置更新后，使用步骤(2)中的约束条件对粒子位置进行处理。

        (5)若达到最大迭代次数,则停止迭代并输出GBMaxiter；否则返回步骤(3)。

5 仿真实验与分析

5.1 NC-OFDM系统参数设置

        假设信道的冲激响应是均值为零的复高斯随机变量，并且是不相关的。在仿真中采用4QAM进行调制，并用信道MSE和误比特率来衡量系统的性能。仿真实验考虑了两种情况：

        (1) 活动子载波是随机产生的。

        (2) 整个频带被划分为几个长度相同的子频带，在每个子频带中有R个子载波，活动子频带的选择是随机的。

        参数设置为：K=256，L=16, P=16,在第2种情况中R=32。N/K=0.5。

        在仿真实验中比较了3种导频设计方法的性能，3种方法描述如下：

        (1)Method A: 等间隔的插入导频,根据频谱感知结果将位于主用户频带内的子载波置零，并选择离它最近的活动子载波作为导频。

        (2)Method B:首先根据频段宽带为每个活动子载波频段分配导频数，然后在各个活动子载波频段内等间隔插入导频序列。

        (3)DPSO algorithm:采用本文提出的离散粒子群算法设计导频序列。

5.2 种群规模M的大小对求解结果的影响

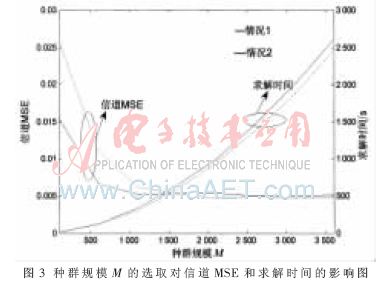
        下面做一数值实验，考察种群规模M的选取对求解结果的影响。由参考文献[6]知，学习因子在[6.4,28]范围内较好,在仿真实验中参数设定c₁=c₂=7,Maxiter=500,SNR=20 dB。

        由图3可知，当种群规模达到1 000时，信道MSE性能趋于稳定，但求解时间却直线上升。因此从性能和效率两方面综合考虑，选定M=1 000。

5.3 仿真结果及分析

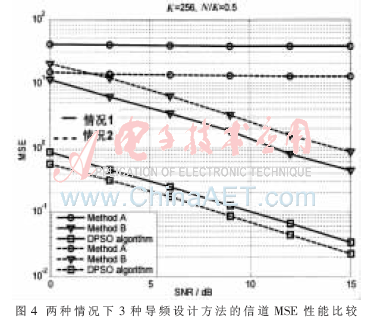
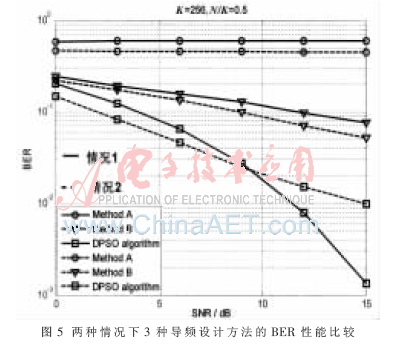
        由仿真结果知，低信噪比时Method B的BER性能与DPSO algorithm的相近，高信噪比时DPSO algorithm的性能优于Method B的。情况(1)下，当SNR为12 dB时,DPSO algorithm的BER性能较Method B提高了60%，信道MSE性能提高了61%。在情况(2)下,SNR为6 dB时,DPSO algorithm的BER性能较Method B提高了70%，信道MSE性能提高了97%。如图4、图5所示。

        由图6和图7知，改变调制方式后，DPSO algorithm的性能仍是最优的。

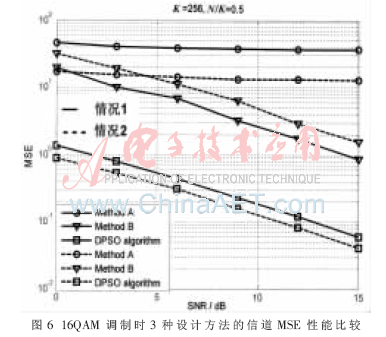
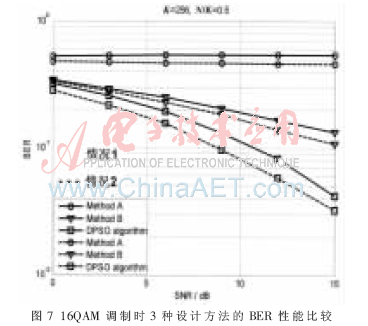
        将NC-OFDM系统的导频设计问题转化为一类确定性的数学模型。该模型与0-1背包问题的数学模型相似，因此可将解决0-1背包问题的离散粒子群算法进行改进，应用于NC-OFDM系统进行导频设计。这种设计方法复杂度较低，程序通用性高。从仿真结果可看出，使用离散粒子群算法设计的导频序列能够获得较好的信道MSE性能和BER性能。

参考文献

[1] 徐昌彪,刘雪亮,鲜永菊. 基于博弈论的动态频谱分配技术研究[J].电子技术应用，2012,38(4):102-105.

[2] COLERI S, ERGEN M, PURI A. Channel estimation techniques based on pilot arrangement in OFDM system[J].IEEE Transaction，2002,48(3):223-229.

[3] BAXLEY R J, KLEIDER J E, ZHOU G T. Pilot design for OFDM with null edge subcarriers[J]. IEEE Transactions on wireless communications，2009,8(1):396-405.

[4] 张佑昌，许小东，戴旭初.一种适用于NC-OFDM系统的次优导频设计[J].通信技术，2010，43(10):1-7.

[5] Hu Die, He Lianghua, Wang Xiaodong,et al. An efficientpilot design method for OFDM Based cognitive radio system[J].IEEE Transactions on Wireless Communications,2011,10(04):1252-1259.

[6] 李兰. 改进的离散粒子群算法求解0-1背包问题[D].广州:华南理工大学,2011.

[7] 尹长川. 多载波宽带无线通信技术[M].北京: 北京邮电大学出版社，2004.

[8] 马慧民，叶春明，张爽.二进制改进粒子群算法在背包问 题中的应用[J].上海理工大学学报,2006,2(1):31-34.