现有的鲁棒数字水印算法^[1-5]在进行所有权鉴别时，通常都是通过计算原始水印与提取水印之间的相关度来进行版权判断,版权检测过程或多或少都需要借助原始载体、原始水印的相关信息，无法实现真正的完全盲检测。

        近年来相关领域提出了自嵌入技术对鲁棒水印算法的研究。参考文献[6]引入自嵌入技术,提出一种DWT-SVD域全盲鲁棒量化水印算法,虽具有良好的不可见性和安全性，但是该算法中水印序列自嵌入对含水印图像提取特征水印序列的最大值有影响，因此提取的嵌入水印序列与认证水印序列之间存在误差。参考文献[7]将自嵌入思想引入到鲁棒水印领域，研究表明该算法在抵抗平滑、添加噪声、JPEG压缩、重采样、剪切和几何攻击上表现出很强的鲁棒性，但是该算法将原始图像每一子块产生的特征水印嵌入到该块的DCT系数中，使得算法对矢量量化等攻击鲁棒性较差。

        本文通过分析与比较，针对前述算法的不足，提出了一种基于非负矩阵分解和提升小波变换的自嵌入盲检测鲁棒数字水印算法。详细介绍了该算法的设计与分析，最后通过实验表明该方案对常见信号处理具有很强的鲁棒性，实现了鲁棒水印序列完全盲检测。

1 算法的分析与设计

        非负矩阵分解(NMF)和提升小波是本文算法的设计基础。对NMF的主要介绍可以见参考文献[8-9]， NMF在某种程度上体现了智能化数据描述的本质。

        提升(二代)小波构造方法由Sweldens提出，与传统小波变换相比，提升格式小波变换不仅克服了传统小波计算量大、不能精确重构原始信号等缺点，而且具有包容传统小波、运算速度快、允许完全原位计算、易于实现并行运算等优点。

        基于上述的理论基础，本文提出了一种自嵌入盲检测鲁棒数字水印算法，算法描述中使用了非负矩阵分解与提升小波的相关术语与符号。该算法包括鲁棒水印序列提取、鲁棒水印序列自嵌入、鲁棒水印序列检测以及认证水印序列提取4个步骤，下面进行详细说明。

1.1 鲁棒水印序列提取

        为便于鲁棒水印序列提取，本文使用小波低频逼近系数均值作为统计特征。该统计特征从逼近信号的小波系数得到，代表原始信号感知上最重要的分量，对于常见信号处理操作具有较强的鲁棒性。而且由于相邻图像像素间具有高度相关性，随机剪切等操作即使引起个别小波系数发生较大的改变，也不会使统计平均值发生很大变化。

1.2 鲁棒水印序列自嵌入

        (5)对嵌入水印序列后的小波低频近似分量进行逆向LWT变换，得到含水印图像I_W。

1.3 鲁棒水印序列检测

        详细水印序列检测过程如下所述：

1.4 认证水印序列提取

         本文设计算法的认证水印序列W"提取过程如下所述：

2 实验结果

2.1 实验参数说明

        仿真实验选用的标准灰度图像Lena、Goldhill、Baboon等作为原始载体图像,实验平台使用Windows XP操作系统和Matlab 7.0编程环境， CPU为Intel CPU E6500 2.9 GHz，内存为4 GB。原始载体进行以Daubchies5/3小波为基的1级LWT,小波低频子带系数进行NMF以产生原始特征水印序列。自嵌入水印序列的长度为1 024 bit。Lena、Goldhill、Baboon 3幅图像的量化步长都为21。

2.2 不可见性实验

        分别从主观与客观测评两个方面衡量算法的不可见性。图1(a)、图1(c)、图1(e)为原始标准测试图像，图1(b)、图1(d)、图1(f)为本文算法下的含水印图像。从图1的实验结果可见,本文设计的算法具有良好的不可见性。客观测评采用峰值信噪比PSNR(Peak Signal to Noise Ratio)，定义如下：

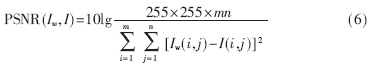
        根据本文算法嵌入水印前后标准测试图像与含水印图像间的PSNR与参考文献[6,10,11]的比较如表1所示。从表1可见，本文算法与同类文献中算法均具有较好的视觉效果。

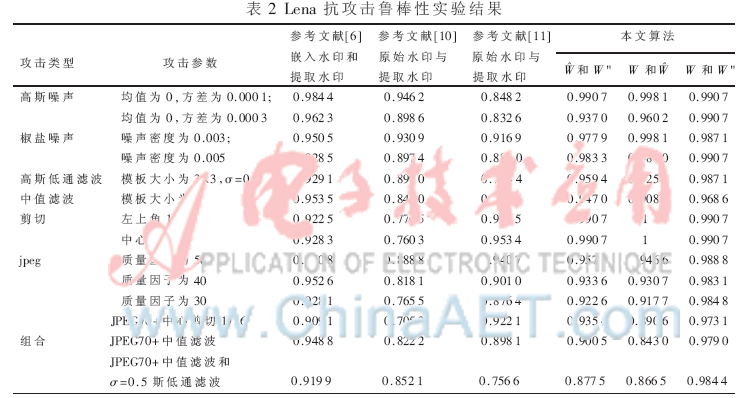
2.3 抗攻击鲁棒性实验结果

        使用归一化相关系数NC(Normalized Correlation)作为算法稳健性衡量指标。本文算法在各种常见图像处理攻击和组合攻击下的实验结果如表2所示。从表2可见，本文算法对常见图像处理攻击和组合攻击均具有较强的鲁棒性，部分性能优于对比参考文献。

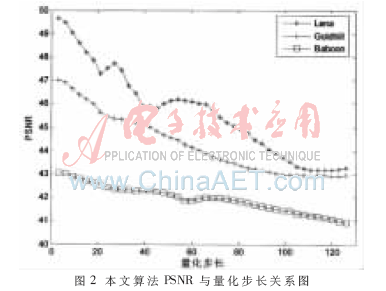
2.4 量化步长选择

        量化步长η的选择决定着算法的鲁棒性和不可见性。η越小，算法的不可见性越好，但鲁棒性越差；η越大，算法的鲁棒性越好，但不可见性越差。图2给出了本文算法PSNR与量化步长之间的关系曲线图。从图2可见，当3幅图像的量化步长η取21时，本文算法具有良好不可见性和较强鲁棒性。

        本文提出了一种自嵌入盲检测鲁棒数字水印算法。实验结果表明，该方案对常见信号处理具有很强的鲁棒性，实现了鲁棒水印序列完全盲检测。此外，本算法还具有计算简单、容易实现等优点，大大增强了其用于数字图像作品版权保护的实用性，具有一定的应用价值。今后的研究将从进一步深入探讨NMF特征序列的稳定性以及分析LWT变换系数特性，设置更合适的量化步长，进一步提高算法整体性能等方面展开。

参考文献

[1] Wang Xiongyang, Hou Limin, Wu Jun. A feature-based robust digital image watermarking against geometric attacks[J].Image and Vision Computing, 2008,26(7):980-989.

[2] Wang Xiongyang, Cui Changying. A novel image watermarking scheme against desynchronization attacks by SVR revision[J]. Journal of Visual Communication and Image Representation, 2008,19(5):334-342.

[3] Li Leida, Qian Jiansheng, PAN J S. Characteristic region based watermark embedding with RST invariance and high capacity[J]. International Journal of Electronics and Communications, 2011,65(5):435-442.

[4] 左姣,范九伦.自嵌入全盲鲁棒水印量化算法[J].微型机与应用,2014,(2):38-40,43.

[5] 冯祥斌,陈永红. 基于纠错编码和RBF神经网络的盲水印新算法[J]. 微型机与应用,2013(7):30-33.

[6] 叶天语.DWT-SVD域全盲自嵌入鲁棒量化水印算法[J].中国图象图形学报,2012,17(6):644-650.

[7] 叶天语.自嵌入完全盲检测顽健数字水印算法[J].通信学报,2012,33(10):7-15.

[8] 刘竞杰, 陶亮.一种基于非负矩阵分解的鲁棒零水印算法[J].计算机工程与应用,2012,48(16):90-93,106.

[9] DONOHO D, STODDEN V. When does non-negative matrix factorization give a correct decomposition into parts[C].Proceeding of Advances in Neural Information Processing Systems, Cambridge: MIT Press, 2004:1141-1148.

[10] 李旭东.基于奇异值分解的灰度级数字水印算法[J].武汉大学学报:信息科学版,2010,35(11):1305-1308,1359.

[11] 李旭东.基于图像能量和量化的公开数字水印算法[J].中北大学学报:自然科学版,2007,28(5):458-461.