文献标识码: A
文章编号: 0258-7998(2014)07-0103-03
在近几场局部战争中,数据链以其独特的战场态势共享、精确指挥控制和武器协同的无缝链接优势,将信息化作战的特点演绎得淋漓尽致[1-2]。对装备数据链系统的作战飞机进行科学合理的效能评估,不仅对武器系统的整体性能提供了衡量标准,而且对其作战过程中的打击效果及作战意图实现提供了量化参考[3]。在作战环境中进行效能评估,将效能评估结果运用到作战实践,构成了航空作战循环体系的全过程。
在现有的文献研究中,针对效能评估或者数据链体制下的效能评估问题,都只是给出一些评估方法或手段以说明不同客体的效能好坏,但是未能将评估结果加以运用;针对航空作战的问题,一种是只注重顶层设计和战法探讨[4],而未考虑到实际效能,有的甚至缺少科学依据,另一种是研究不同作战条件下的作战兵力变化情况[5],而数据链的作用和作战武器系统的效能考虑较少。这些基本上都只是在一个侧面对航空作战问题进行研究,对实现和把握航空作战一体化进程的全要素分析还有一定差距,“由作战到评估效能,再由评估结果到作战运用”的环路尚没有有效衔接起来。本文研究就是要实现效能评估与作战运用的一体化。
1 飞机作战的平均战斗力水平
1.1数据链体制下的飞机效能评估
在效能评估中,飞机的空战能力指数可以采用对数法表示为[6]:
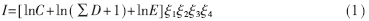
其中, I为空战能力指数,C为机动性参数,D为火力参数,E为探测目标能力参数,ξ1为生存力系数,ξ2为电子对抗能力系数,ξ3为航程系数,ξ4为飞行员操纵效能系数。
加入数据链后新的空战能力可表示为:
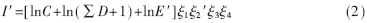
其中, E′和ξ2′分别表示经数据链提升后的探测能力和电子对抗能力,且E′=E+λ1E, ξ2′= ξ2+λ2ξ2,λ1和λ2表示提升率。
对于λ1的确定,考虑一种简单的双机协同作战情况。假定双机为同向直线飞行,则λ1用探测面积的变化比来表示为:
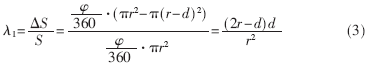
式中φ为雷达搜索方位角,r为雷达探测距离,d为机间距离(d<r)。
对于λ2的确定,在参考文献[7]中,给出了机载电子对抗设备的电子对抗能力,全向雷达告警系统为1.05,全向雷达告警+消极干扰投放+导弹逼近警告的综合系统为1.16~1.20,有数据链支撑下的电子对抗设备,还会增加积极干扰投放功能,所以对其赋值时可以使其大于无数据链时的电子对抗能力。
1.2 空战能力指数到平均战斗力水平的转化
作如式(4)的变换,将I(I>>1)变换为在区间(0,1)上的平均战斗力水平γ(k为一比例调节因子且k>0,作用是避免变换后的γ在数值上过于集中)。
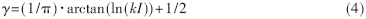
现证明γ和I关于空战能力的描述是等价的,且γ和I具有一致性。
证明 令A={x|x∈Z, x>0}, B={x|x∈Z, 0<x<1}, 作由A到B的映射:
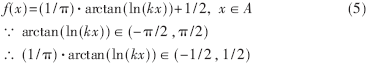
进而, (1/π)·arctan(ln(kx))+1/2∈(0,1)
所以f: A→B是由A到B的一一映射,这说明A和B是等势(等价)的,即A~B。
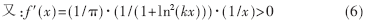
即f(x)为增函数,说明γ和I的增减变化关系一致。所以,γ在保证空战能力指数特性的情况下,可以用来作为平均战斗力水平。
2 空战中的兵力变化建模
本文的建模将以蓝彻斯特方程的分析方法为基础,首先给出蓝彻斯特平方律方程的表达式为:

式中R、B为红、蓝方在时刻t的战斗单位数量,α、β为蓝、红方每个战斗单位的平均战斗力水平。
对上式进行等式相除后并积分,得:

令x=1-R/R0表示红方兵力的消耗率,y=B/B0表示蓝方兵力的剩余率。L=β·R02/α·B02表示红、蓝方的战斗实力之比。将式(8)变形,用x、y、L代入得:

考虑飞机在配备有数据链情况下的作战方程。首先求解平均战斗力水平的提升率ηR和ηB,即有ηR=(γR′-γR)/γR,ηB=(γB′-γB)/γB。
在空战中性能更优功能更强大的数据链拥有方可以在交战中获利,为此计算一数据链水平占优因子,将其定义为:

这样将数据链体制下的双方兵力变化规律建模为:
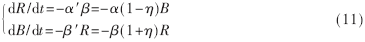
按照式(7)~(9)的分析,仍可得红方消耗率与蓝方剩余率的变化关系:
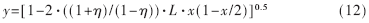
此处(1+η)/(1-η)·L部分定义为等效实力比。
在有增援的情况下建立空战模型为:
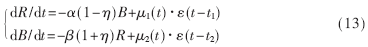
式中μ1(t)、μ2(t)表示双方的增援率,t1、t2表示增援开始时刻,ε(t)表示阶跃函数。若在战斗中存在非战斗减员的情况,空战模型扩充为:
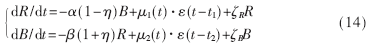
其中ζR和ζB分别表示红、蓝方的非战斗减员系数。
3 仿真实验
假定红、蓝方所用机型分别为米格-29和F-15E。米格-29中r=90 km,令d=70 km时,则可求λ1=0.95。设定红、蓝方电子对抗能力为1.05和1.2,红方经数据链提升后变为1.8。效能评估指标中的其余参数见参考文献[6],求解空战能力指数(k取1/10)和平均战斗力水平,如表1所示。

3.1战斗实力比对双方空战力量的影响
取一组L=[0.6;0.8;1;1.2;1.4],由表1可知η=0.21,由此仿真得到双方的消耗率与剩余率曲线(图1)。
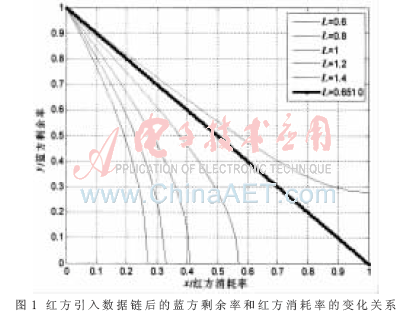
由图知当L介于0.6与0.8之间时,达到双方的实力平衡。令等效实力比(1+η)/(1-η))·L=1,可求得L=0.65。这说明由于数据链的采用,红方只要大于蓝方实力的65%就可以获胜。图1中也专门绘出了双方实力的平衡的分界线。
3.2增援模型中不同增援时刻点对空战的影响
设定增援率为2.5,且令t1=0,其他仿真参数不变,得双方的动态损耗图如图2所示。
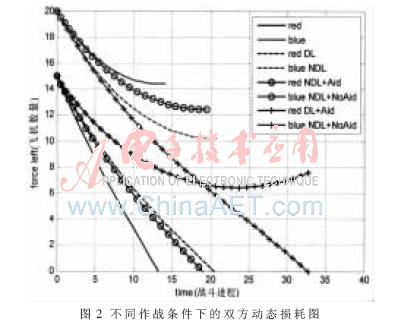
图2中4种曲线分别为原始作战状态、红方有数据链支持、红方有支援但无数据链支持、红方有数据链支持和增援。曲线说明在数据链体制下,红方在增援力量帮助下可以最终获得胜利。
接下来确定红方有效的增援时间范围。令t1分别为0、4、8和12,得双方的兵力变化曲线如图3所示。
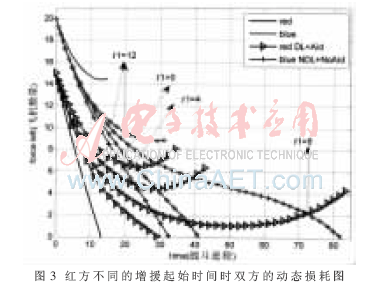
t1=12时,增援太晚已不能改变红方失败的结果。说明在有增援的空战中存在一个增援的时间分界点,在此之前增援可以扭转双方战局;反之不能改变战局。在本文参数下,经多次仿真确定有效增援的时间范围为[0,9.5]。
让t1在[0,9.5]间取值,步进量为0.5,得到的双方动态损耗曲线如图4所示。
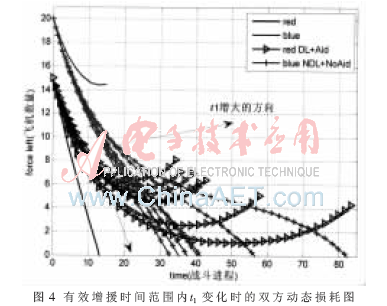
由图知当t1增大时,总趋势是空战进程维持时间越长,战斗胜利时红方剩余的飞机数量越少。为分析不同t1时的作战效率,这里给出随t1值不同时红方增援和损失飞机数量变化如图5所示。
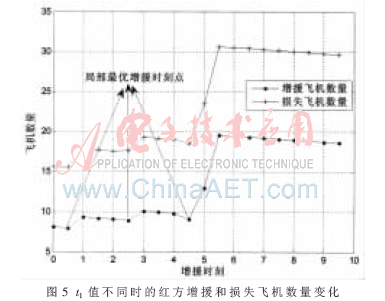
当t1变化时,增援和损失飞机数不是单调递增关系,而是存在一系列极小值点,在这些点周围增援和损失的飞机数都较大。据此可得,在不同的增援时刻,存在使得增援和损失飞机数同时较小的局部最优点,本文称为“局部最优增援时刻点”。掌握了该时刻点,便于指挥员对增援时机进行把握。
对数据链体制下的飞机效能评估及其航空作战运用进行了研究。给出了数据链体制下的飞机效能评估的计算方法,建立了反映数据链功能的航空作战兵力变化模型,并考虑在有增援模式时的模型变化。仿真分析了等效实力比和数据链对空战的影响,在有增援力量加入的作战中,存在“局部最优增援时刻点”,对于空战决策部署具有借鉴意义。
参考文献
[1] Zhou Lei, Zhang Hanyi, Wang Tao, et al. Static check of WS-CDL documents[J]. IEEE International Symposium on Service-Oriented System Engineering, 2008(8):142-147.
[2] 曾国奇,李思吟,韦志棉,等.箭载共形相控阵卫星数据链通信仿真研究[J].电子技术应用,2012,38(11):104-107.
[3] 黄俊, 孙义东, 武哲,等. 战斗机对地攻击作战效能分析[J]. 北京航空航天大学学报,2002,28(3):354-357.
[4] 苏荣,满广志,奚丹.空天一体作战初级阶段的典型作战运用[J].导弹与航天运载技术,2009(2):20-24.
[5] 王安丽,何胜强,张安.机群编队对地攻击飞机武器系统作战模型研究[J].飞行力学,2005,23(1):82-85.
[6] 黄金才,张勇,杨磊,等.战术数据链作战效能定量评估方法[J].火力与指挥控制,2010,35(12):66-69.
[7] 朱宝鎏,朱荣昌,熊笑非.作战飞机效能评估(第2版)[M].北京:航空工业出版社,2006.

