基于Matlab的模拟滤波器设计与仿真
来源:现代电子技术
摘要: 建立在拉普拉斯变换基础之上的模拟滤波器的理论和设计方法已经发展得相当成熟,且有若干典型滤波器供人们选择,如巴特沃斯(But-terworth)滤波器、切比雪夫(Chebyshev)滤波器等。但是关于滤波器实现的电路元件参数的选取和计算却是件繁琐的工作。在此提出基于Ma-tlab将电路参数计算程序化的方法,并通过效果仿真达到优化电路参数的目的,而且程序具有扩展功能。
Abstract:
Key words :
0 引言
建立在拉普拉斯变换基础之上的模拟滤波器的理论和设计方法已经发展得相当成熟,且有若干典型滤波器供人们选择,如巴特沃斯(But-terworth)滤波器、切比雪夫(Chebyshev)滤波器等。但是关于滤波器实现的电路元件参数的选取和计算却是件繁琐的工作。在此提出基于Ma-tlab将电路参数计算程序化的方法,并通过效果仿真达到优化电路参数的目的,而且程序具有扩展功能。
l 模拟滤波器的设计流程
模拟低通滤波器的设计指标有ap,Ωp,as,Ωs,其中Ωp和Ωs分别为通带截止频率和阻带截止频率;ap是通带Ω中最大衰减系数;as是阻带Ω≥Ωs的最小衰减系数ap和Ωs一般用dB表示。在此希望幅度平方函数满足给定的技术指标ap,Ωp,as,Ωs。
(1)巴特沃斯滤波器
幅频特性模的平方为:

式中:N为滤波器的阶数;wc滤波器截止角频率。
(2)切比雪夫滤波器
(2)切比雪夫滤波器
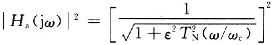
式中:ε决定通带内起伏大小的波纹参数;TN为第一类切比雪夫多项式:
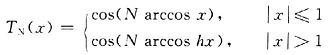
LC一端口网络的T型电路和∏型电路对应不同的Ha(s)函数的连分式展开形式。在设计时,先求出归一化低通元件值,然后反演出电路元件实际值。
2 运用Matlab编程实现的模拟电路设计并仿真
(1)无源单端口模拟滤波器的设计举例
技术指标:
通带内允许起伏:-1 dB,O≤Ω≤2 π×104 rad/s;
阻带衰减:≤-15 dB,2 π×2×104 rad/s≤Ω<+∞:
信源内阻Rs和负载电阻RL相等,均取600 Ω。
运用Matlab语言进行编程计算出如图1所示巴特沃斯T型和∏型电路图的电路元件参数。图2为切比雪夫T型和∏型电路图的电路元件参数。
2 运用Matlab编程实现的模拟电路设计并仿真
(1)无源单端口模拟滤波器的设计举例
技术指标:
通带内允许起伏:-1 dB,O≤Ω≤2 π×104 rad/s;
阻带衰减:≤-15 dB,2 π×2×104 rad/s≤Ω<+∞:
信源内阻Rs和负载电阻RL相等,均取600 Ω。
运用Matlab语言进行编程计算出如图1所示巴特沃斯T型和∏型电路图的电路元件参数。图2为切比雪夫T型和∏型电路图的电路元件参数。
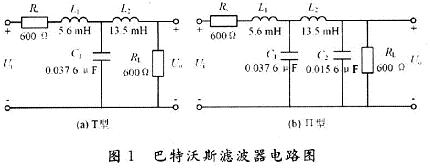
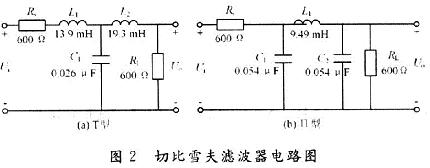
图3为设计巴特沃斯T型和∏型电路图输出电压幅频特性Matlab仿真图。图4为切比雪夫输出电路幅频特性Matlab仿真图。
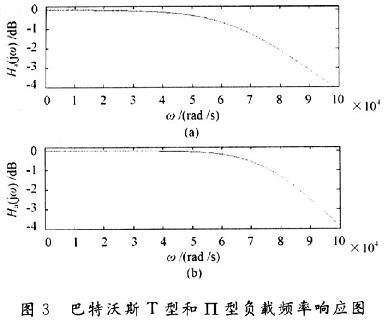
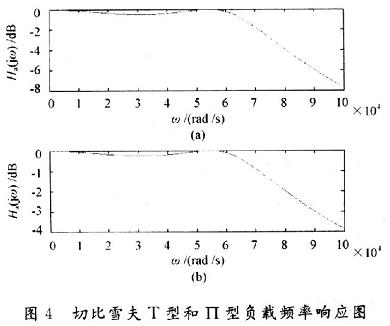
图3表明曲线呈调下降,随着角频率Ω的增大曲线接近于零,所设计巴特沃斯电路满足参数要求;图4表明,曲线变化是不均匀的,在Ω<Ωc内幅度的变化是按一定比例的,在Ω>Ωc这段上是单调下降的。切比雪夫电路的幅频特性比巴特沃斯电路的幅频特性有较窄的过渡特性。
(2)程序描述

3 结语
本文采用反卷积的方法实现了将一个多项式用连分式表示出来的系数提取方法,将T型和∏型考尔电路设计程序化,减轻了繁琐运算的劳动负担。所编写程序易于扩展,仿真结果表明所设计电路符合技术指标,程序正确。
本文采用反卷积的方法实现了将一个多项式用连分式表示出来的系数提取方法,将T型和∏型考尔电路设计程序化,减轻了繁琐运算的劳动负担。所编写程序易于扩展,仿真结果表明所设计电路符合技术指标,程序正确。
此内容为AET网站原创,未经授权禁止转载。

