0 引言

    上世纪70年代，研究人员开始了对无线移动自组织（Ad hoc）网络技术的开发，当时是因美国出于军事需要而开始研究无线网，让其能适应战场的需要进行数据通信。Ad hoc网络与以往的无线网格有着明显的不同，它的网络结构是随意的、非固定的。与此同时，它也不需专门固定的基站或路由器当做管理中心。到了上世纪末，研究无线移动自组织网络的工作就已经在世界各国开始陆续展开，并且从无线通信领域里的一个分支，慢慢扩大到一个单独的领域。当前关于Ad hoc网络的学术会议越来越多。由于移动自组网络的任意一节点都能随机移动，因此组网非常灵活，那么相应的网络开发的难度就大大增加了^[1]。当前研究^[2-3]中遇到了Ad hoc网络发展瓶颈：移动节点在子网中进行切换过程中，基本上无法避免通信中断，而且还会带来很大的延时。上述问题急需对其移动的方位完成评估及确定所需链接的路由器，这样即可让移动节点时刻做好发生切换的预备工作，进而缩短或避免中断，并做好延时，争取时间^[4]。处理这一问题的广泛处理方式是采用人工神经网络，然而人工网络模型固然可构造出相对更精确的分类界面，但仍需非常多的训练数据才可做参数估计，并且运算相对复杂，收敛较慢^[5]。本文针对上述问题，进行了一种对移动节点的路径新预测模型设计，采用了隐马尔科夫模型（HMM）处理，这一研究对于Ad hoc网络实际应用的拓展具有一定的价值。

1 HMM实现Ad网络问题处理

1.1 3个基本问题的求解实现

    在确定HMM模型情况下，需要实现以下3个关键问题才可以较好地运用在实际项目中：(1)如果指定的一组观察序列O=O₁，O₂，…，O_T、模型λ=(A，B，π)，在此条件下，怎样科学合理地运算出概率P(O|λ)；(2)条件与(1)相同，怎样选取一个对应的状态序列S=q₁，q₂，…，q_T，S可以非常明晰地阐述O；(3)怎样调整模型参数λ=(A，B，π)，能够满足P(O|λ)最大。通常情况下，这3个问题都是在一个实际项目的应用中被总结出的。

    解决问题(1)的方法：若直接做运算，即：

    若按照该方法直接运算，就会用到全部可能的状态序列，复杂度以及指数巨大，运算难度相对高，所以就会采用前向的方法进行运算。前向算法做运算，首先要定义前向变量α_t(i)：

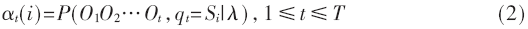
    在已知的模型λ前提下，从最初时刻到时刻t局部的观察序列O₁O₂…O_t，和时刻t状态S_i形成的概率为α_t(i)。解决问题(2)的方法：使用Viterbi Algorithm方法是一个比较好的选择。这里，将Viterbi变量定义为：

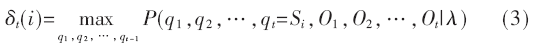
    δ_t(i)是已知的观察序列，从最初时刻到t时刻，同时最大概率状态序列的状态是S_i。其中，φ_t(i)是概率最大途径中此刻状态的之前状态。求解问题(2)的步骤是：

    (1)初始化

    解决问题(3)的方法：实质上即是求解HMM模型参数做优化处理的问题。如今已有的大量算法都能够解决该问题，本文通过使用Baum Welch算法，同时将变量定义成：

    按照上述的运算方式，即可推出：

    把新模型参数当做是现存模型参数，重复前面的步骤，一直到能获得最优的HMM模型参数，这样问题就迎刃而解。

1.2 移动节点观察模型的设计

    若有一移动节点MN，它在与自己已建立无线连接的接入路由器AR所覆盖的无线信号区域内移动，可定期对信号强度等有关移动路径的信息进行测量。假设MN处在离散时间nΔt(n=1，2，…)时，能够测得与AR之间的信号强度，还能够得到按照信号强度为观察值的观察序列O₁，O₂，…，O_T。若Δt很小，则可看成该时间段里，MN移动的速度是一个不变的值。可将该定值用v_n(n=1，2…)来表示。为使移动预估目标MN进入子网，所以会将AR涉及到的范围区域分块成一些子域，见图1。此外，还要使得每个子区域所包涵的范围都满足r₁=r₂=…=r_N。还将该子区域当成MN移动的过程中的每一种状态Qi，i=1，2，…，N。若MN按照其中一路径进行移动，那么可以得到其观察序列是O=O₁，O₂，…，O_T，如图1所示。因为一些因素会使得观察序列是随机的。其一，是在观察的最初时间就不具备确定性，MN移动速度的随机性也会影响观察位置的确定；其二，由于存在噪音、测量方式的错误等原因，会导致观察值存在误差；其三，即使MN会按照某种路径移动，可移动在某种程度上还是随机的。

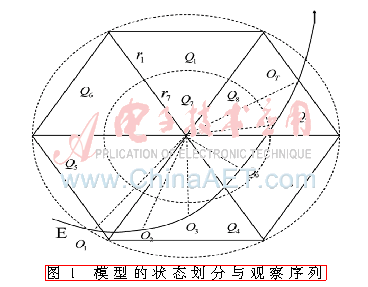
    假设M为此时AR的邻居子网数，对于离散参数的HMM初始值只有一个，即统一分布，所以，模型的初始值的设置方法可以表述成MN按照等概率的方式从一状态切换成另一种邻近的状态，以获得λ_ij=(A_ij，B_ij，π)，1≤i，j≤M，A、B、π分别代表状态转移概率矩阵、符号输出概率矩阵、初始状态分布。在进入AR时，对于之前属于AR的哪个邻居子网，MN是可以知道的，假设是子网Θ，通过AR，MN可以得到HMM模型集{λ_Θj|1≤Θ≤M，j=1，2，…，M}。如果MN得到了观察序列，则按照以下公式进行计算：

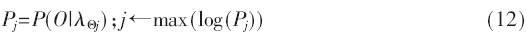
    此时，j为AR的邻居子网，也就是MN接下来要进入的子网。训练、观察、判别是以上预测模型的预测过程，通过Baum Welch算法求解训练过程，若观察序列就是因已经指定的模型而形成的，那么这种算法的效果是能够达到的，这在多个领域(如语音识别)已被证实，所以，模型训练所采用的是Baum Welch算法。MN移动预测模型的预测判别方法主要是找出一个模型λ_x，使得P(O|λ_x)最大。

    离散HMM训练样本及其可取值空间并不是无限的，但上面提到在一定范围内，MN移动预测HMM模型中的观察值任意取值，所以一定要先将观察序列在观察符号空间进行量化，再对观察值与观察符号输出概率之间的关系进行确定。图2是观察符号空间与量化的过程图。观察符号空间的确定所采取的是径向划分法，也就是将AR作为中心，在其径向上的各状态范围内进行等间隔区域的划分，同时，将中心信号的强度值作为观察符号空间中的符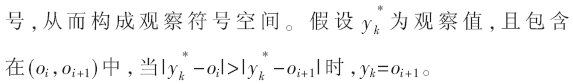

    虽然在量化过程中会有一定的误差，但经过量化的观察值对应的状态和符号输出概率是不变的，所以，量化误差对于与MN将连接的AR的预测并无太大影响。

2 设计模型的抗毁性分析

    在Ad网络系统中，抗毁性是一个最为关键的特点，抗毁性强弱所体现的是对某些节点之间的通信进行中断所需破坏的链接数。主要从两个角度来分析抗毁性，即黏聚度与连通度。这里仅分析去掉部分节点后的网络连通度。通常情况下，网络的连通度越好，其抗毁性就越强，反之则亦然。

2.1 信道抗毁性

    通过计算机的帮助可获得区域划分方式，采用有湖与无湖两种划分方式进行对应的信道模型方案的结果表述，如图3、图4所示。

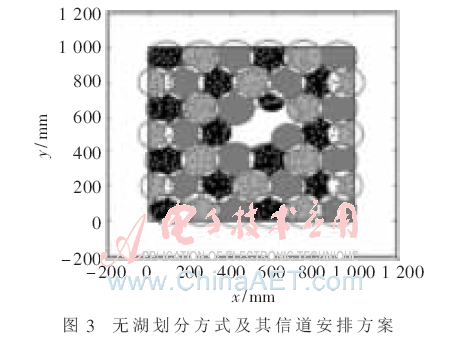
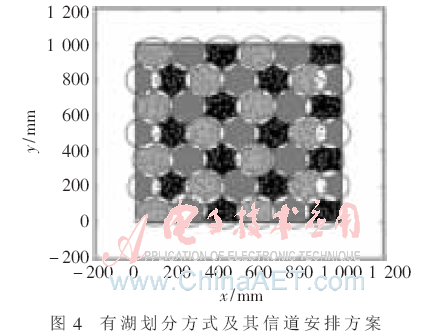
    图3、图4可得，此时最小半径相加所得总和分别为4034.4、4213.5。研究表明，只需要最小半径相加小于10 000，则Ad网络的连通性是良好的，即抗毁性较强。图中结果表明了模型的抗毁性优势。

2.2 网络的连通度

    定量原理：假设有一无向图G，那么G为k的连通图的充分必要条件是：G的定点数不小于k+1。在任一通信区域中，假设这个区域有M个节点，k是其连通度，那么区域连通的充要条件是：M不小k+1；926是正方形通信区域附表中所定的节点数，那么其连通的充要条件是：

    只要节点的连通度不超过925，通信网络就是连通的。根据数学概率理论可将网络节点的连通概率计算出来。随机将节点集合中的2%、5%、10%、15%等数量的节点去掉，由设计模型可得到当前网络的连通度，那么网络节点的连通概率也就可以计算出来了。表1所描述的是其抗毁性算法应用的节点数。

    由表1可见，节点的数量与抗毁性的强度是成正比的，相交面积大小与抗毁性的强度成反比。同时由原理可知，设计模型的Ad Hoc网络具有较强的抗毁性。

    由以上分析可知，节点最多的是公共区域，其网络连通性比较强，设计模型的Ad Hoc网络具有较强的抗毁性，同样解决了Ad Hoc网络的延时问题。

3 结论

    作为一种随机概率模型，HMM表示的是与时间序列有关联的有效模型，所涉及的知识包括概率与统计学，目的是对参数不同的短时平稳信号段进行识别，并实现信号之间的转化，该模型应用中的一切实际问题均能以HMM模型中的3个问题来表示。在这里，采取仿真对HMM预测移动进行了可行性研究，在训练样本以及初始模型参数已知的前提下，采取新的数据来检验模型，从而确定模型预测的准确度。由仿真结果可知，该模型是可行的，且抗毁性具有一定的优势。

参考文献

[1] Wang Hao，Liu Nan，Li Zhihang，et al.A unified algorithm for mobility load balancing in 3GPP LTE multi-cell networks[J].Science China(Information Sciences)，2013，56(2)：118-128.

[2] Zhang Zhongshan，Huang Fuwei，Long Keping，et al.On the　designing principles and optimization approaches of bio-in-spired self-organized network: a survey[J].Science China(Information Sciences)，2013，56(7)：5-32.

[3] Dan Yangqin，Hong Weili，Lin Ma，et al.An ant colony algorithm based congestion elusion routing strategy for mobile　ad hoc networks[J].Journal of Harbin Institute of Technology，2013，20(3)：99-103.

[4] WAKAMIYA N，LEIBNITZ K，MURATA M.Biologically　inspired self-organizing networks[J].智能系统学报，2009，4(4)：369-375.

[5] 李曦.Always-optimally-coordinated candidate selection algorithm for peer-to-peer files sharing system in mobile self-organized networks[J].High Technology Letters，2009，15(3)：281-287.