摘  要： 提出了一种改进的多群协作粒子群优化算法，该算法整个种群采用主从模式，分为一个主群和多个从群，多个从群粒子统一地进行初始化操作，从而避免了多个粒子群重复搜索现象。同时，算法采取了一种扰动策略，即当前全局最优解在扰动因子的迭代周期内保持不变时，就重置粒子的速度，迫使粒子群摆脱局部极小。该算法不仅增加了种群的多样性，扩大了搜索范围，而且还改善整个种群易陷入局部极小值的缺陷。通过9个基准函数进行测试，实验结果表明，IMCPSO与MCPSO算法相比具有明显的优越性。

　　关键词： 多群协作；粒子群优化；函数优化

　　粒子群优化PSO（Particle Swarm Optimization）算法，由KENNEDY J和EBERHART R C[1-2]于1995年提出，成为智能计算领域的研究热点之一。PSO算法是一种模拟自然生物界鸟群或鱼群行为的随机智能优化算法，其全局搜索能力较强，对一些粒子进行迭代计算获取全局最优解。PSO算法是一种模拟自然界鸟群或鱼群行为的随机智能优化算法。不少学者们也研究了一些改进算法来改善PSO算法的性能和收敛速度。牛奔[3]等基于种群共生关系提出了多群协作粒子群优化MCPSO（Multi-swarm Cooperative Particle Swarm Optimizer）算法的两种进化结构。而ZHAO S Z等[4]在2011年提出了关于动态拓扑结构的多粒子群协同优化算法。KONSTANTINOS E P[5]提出了主-从模式的并行微型结构的多粒子群协同优化算法。

　　但是这些多粒子群优化算法可能存在重复搜索，造成粒子数目的浪费，同时又在多维数、多峰值优化函数存在算法求解精度低及收敛度差等不足，为此本文提出一种改进的多群协作粒子群协同粒子群优化（IMCPSO）算法。该算法对从群粒子采取统一初始化操作，避免在搜索初期造成的重复搜索现象。同时，引入粒子扰动策略，即当粒子陷入局部极小值时能够重新设置粒子速度，强制粒子摆脱陷入局部极小值的可能。

　　实验仿真结果表明，IMCPSO算法比MCPSO和PSO算法在寻优精度和收敛速度都有大幅度的提高，并且具有较强的鲁棒性。

1 基本粒子群优化算法

　　基本PSO算法利用单个粒子间的协作和竞争来搜索优化问题的最优解。算法起初通过随机生成初始化种群粒子，其中每个粒子作为优化问题的一个候选方案，并由目标函数计算出粒子适应值。种群粒子在搜索空间里运动，通过自身速度向量来判定其运动的方向和长度。每个粒子跟随当前自身最优位置和种群的最优位置而运动，最后经过多次搜索得到优化问题的最优解。

　　假设在D维搜索空间里，粒子搜索空间的上、下界分别为xmax、xmin。第i个粒子的位置和速度矢量分别为xi=（xi1，xi2，…，xiD），vi=（vi1，vi2，…，viD），其中xiD∈（xmax，xmin），d∈[1，D]。Pi=（pi1，pi2，…，piD）表示为第i个粒子的当前最优位置矢量，Pg=（pg1，pg2，…，pgD）是种群的全局最优位置矢量。每次迭代过程中，粒子的速度和位置的更新公式为：

　　Vid（t+1）=wvid（t）+c1R1（pid-xid（t））+c2R2（pgd-xgd（t））（1）

　　xid（t+1）=xid（t）+vid（t）（2）

　　其中，w为惯性权重，c1、c2为加速因子，R1、R2为[0，1]之间的随机数[1]。

　　通过解析式（1）和（2）可以发现，经典的PSO算法的种群粒子在不断的搜索过程中，常常跟踪当前全局最优位置及自己目前搜索到的历史最优位置。因此，粒子速度比较快地下降接近为0，造成种群粒子陷入局部极小值而无法摆脱。这种“趋同性”局限了粒子的搜索空间，若实现搜索空间的扩大，必须要加大种群的粒子数，或降低种群粒子对全局最优位置的追踪。加大粒子数会造成优化问题的计算复杂度的增加，降低种群粒子对全局最优位置的追踪又造成算法收敛性能较差的不足。

2 一种改进的多群协作粒子群优化算法

　　2.1 MCPSO算法

　　牛奔[3]等人提出的基本MCPSO算法，借鉴了生物系统中的共生现象，反映了种群个体之间的相互关系。该算法将种群均分成具有主从模式的一个主群和多个从群，利用主、从群间的共生关系，两者进行信息的交流与传递，某种程度上克服了粒子陷入局部最优的危险。根据不同的共生关系，算法可分为合作（COL_MCPSO）和竞争（COM_MCPSO）两种形式，算法中每个从群都独立并行地执行基本PSO算法或其变体，更新粒子的位置和速度。当所有从群更新完成，再将局部最优值传给主群。

　　（1）COL_MCPSO算法主群粒子位置、速度更新公式为：

　　2.2 IMPSCO算法

　　面对高维、多峰值的复杂优化问题，为了获得更好的全局最优值，基本MCPSO算法通过牺牲收敛速度来增加种群多样性，以达到降低种群陷入局部极小值的可能。但是同时保持种群多样性和较快的收敛速度，仍然是目前优化算法面临的一个挑战，并且在搜索初期，多种群并行独立搜索解空间，造成部分粒子的重复搜索现象，且种群搜索初期容易陷入局部最优解。

　　2.3 改进算法

　　针对上述算法不足之处，本文通过基本MCPSO算法中竞争结果，即以COM_MCPSO算法为主要研究算法，提出了一种改进的多群协作粒子群优化算法。该算法利用一个主群和多个从群结构协作进化，其中从群粒子根据本粒子群迄今搜索到的最优位置来更新种群中粒子速度，而主群是由所有从群的当前全局最优位置来更新主群中的粒子速度。多个从群改善了寻优搜索过程中，提高种群多样性，扩大了解空间内的搜索范围。同时，主群粒子追逐当前的全局最优位置来提高该算法的收敛速度，从而兼顾优化过程的精度和效率。这种算法各从群粒子数目并不要求相同，每个子群的粒子位置和速度的更新策略也可以不同。当粒子数目相等的情况下，IMCPSO与基本MCPSO算法的计算复杂度是相同的。

　　该算法提出增加扰动因子的策略，即假设目前寻优得到的全局最优位置在连续的l次迭代都没有更新，则在搜索空间内重新赋值粒子速度。l为自然数，本文中称作扰动因子。其扰动策略的更新公式为：

　　if t-tl>l then reset v；

　　其中tl表示为主群当前更新到全局最优位置的迭代步数。

　　扰动策略的原理为：假如种群陷入局部极小值时，重新随机化粒子速度，迫使种群粒子跳出局部极小值，进而进行下一迭代的新的搜索过程。IMCPSO算法利用扰动因子的策略，能够进一步提高MCPSO算法的性能。

　　IMCPSO算法的步骤：（1）设置算法参数大小，初始化主群和从群粒子的位置和速度。（2）评估主群和从群中每个粒子的适应值，求解各从群的全局最优值及整个种群的全局最优位置。（3）利用式（1）、（2），更新全部从群粒子，并评估从群的各粒子的适应值。（4）将从群的全局最优位置传给主群，并根据式（5）、（6）更新主群的各个粒子，然后评估主群各粒子的适应值。（5）假如t-tl>l1主群全局最优位置未更新则执行步骤（6），否则执行步骤（7）。（6）在搜索空间内重置主群粒子速度。（7）若满足终止条件（达到最大迭代步数）终止，返回主群的全局最优值及适应值；否则返回步骤（3）。

3 实验设计与结果分析

　　3.1 基准函数

　　为了保证实验对比的准确性，IMCPSO和MCPSO算法参数设置为一个主群和4个从群，每个子群粒子个数为5，c1=c2=c3=1.494 45，wmin=0.4，wmax=0.9，其中vmax限制为搜索范围的20%。扰动因子l=10。

　　本文比较了IMCPSO与经典PSO算法、基本MCPSO算法，使用9个经典的基准函数评估所提算法的性能。测试基准函数与搜索范围如下。

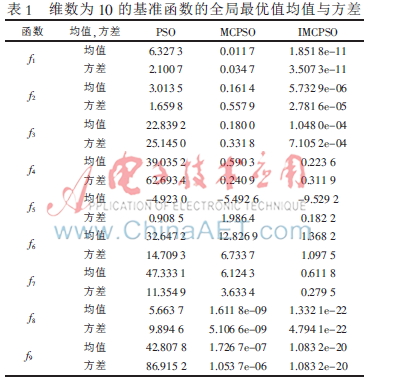
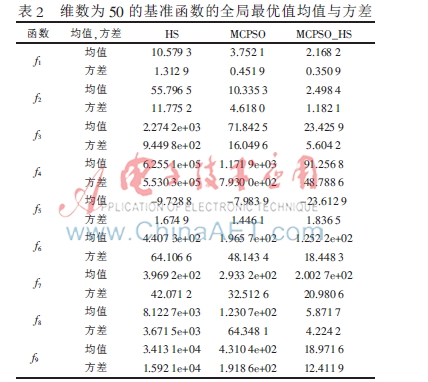
　　每个算法分别在维数为10、50的基准函数上测试，迭代次数为1 000次，运行100次。如表1、表2中实验结果为种群全局最优值的均值和标准差，IMCPSO和MCPSO-HS列代表函数相应的全局最佳适应值，所有结果的表达形式为“0.0000e+00”。IMCPSO算法的最佳适应值平均值与标准差要好于PSO和MCPSO算法，说明所提算法具有较好的稳定性。

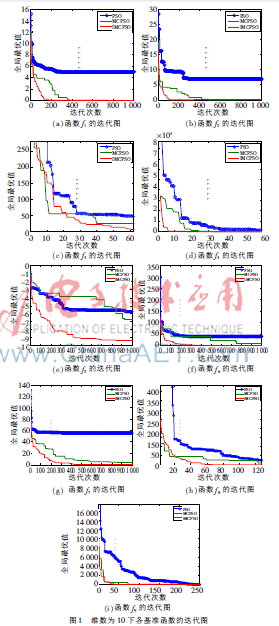
　　为表明算法的收敛速度，在Windows7系统、Intel（R）4 3.20 GHz CPU、2 GB RAM、软件为MATLAB 2012a的环境下运行所提算法，并得出在维数为10下各基准函数的迭代过程，如图1所示。可知IMPSCO算法的收敛速度和最优值明显优于PSO和MCPSO算法。

　　本文中IMCPSO算法通过多个从群改善种群多样性，扩大了搜索范围，通过统一的初始化操作，避免了搜索空间的重复搜索。该算法引入扰动策略，进一步避免了种群粒子陷入局部最优点的危险。实验结果表明，与PSO和MCPSO算法相比，IMCPSO算法更有效地使用了以往的解决方案，以便获取较好的全局最优位置。通过测试的9个基准函数，可以得出IMCPSO算法在解决高维、多峰值复杂优化函数改善了PSO和MCPSO算法的寻优性能和求解精度，且具有较强的鲁棒性。

　　参考文献

　　[1] KENNEDY J， EBERHART R C. Particle swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks， piscataway， 1995： 1942-1948.

　　[2] EBERHART R C， KENNEDY J. A new optimizer using particle swarm theory[C]. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. 1995（1）： 39-43.

　　[3] Niu Ben， Zhu Yunlong， He Xiaoxian， et al. MCPSO： A multi-swarm cooperative particle swarm optimizer[J]. Applied Mathematics and Computation， 2007， 185（2）： 1050-1062.

　　[4] ZHAO S Z， SUGANTHAN P N， PAN QUAN-KE， et al. Dynamic multi-swarm particle swarm optimizer with harmony search[J]. Expert Systems with Applications， 2011， 38（4）： 3735-3742.

　　[5] KONSTANTINOS E P. Parallel cooperative micro-particle swarm optimization： A master-slave model[J]. Applied Soft Computing， 2012， 12（11）： 3552-3579.