文献标识码: A
文章编号: 0258-7998(2015)05-0077-04
0 引言
电机振动信号的观测数据中包含着大量的特征信息,为了能有效地提取有用的特征信息,需要对电机振动信号进行降噪处理。傅里叶变换不能逼近电机振动信号的局部信息,不适用于电机振动信号的降噪处理[1]。小波函数具有局部分析功能,能够非常好地逼近信号的细节特征,便于电机特征信息的提取。文献[2]提出的快速小波分解算法使得小波在多个领域得到了广泛应用,在此基础上,小波阈值降噪也得到快速发展。
文献[3]提出了小波阈值降噪算法,其原理是信号和噪声在小波域中呈现着不同表现形式,随着分解尺度的增加,噪声系数的幅值快速衰减逼近于零,而真实信号系数的幅值保持不变[4]。在阈值降噪的过程中,阈值和阈值函数的选择是重要的一步。目前Bayes阈值是比较受欢迎的阈值选取方法之一。
Bayes阈值降噪的原理是在假设小波系数服从广义高斯分布的前提下,通过最小化贝叶斯风险估计得到优化阈值,这是目前很多专家学者选择较多的阈值选取方法之一[5,6]。本文同样选用Bayes阈值,根据不同分解尺度上信号和噪声能量分布不同的特点对Bayes阈值进行改进,这样阈值的选择更符合噪声在各层的分布情况[7]。同时,由于硬阈值函数是一种不连续函数,导致重构的信号具有振荡性,软阈值函数对信号作收缩处理与信号的真实值存在偏差[8,9]。针对上述不足,本文提出改进的阈值函数算法,使用改进阈值函数结合新阈值对小波系数进行修正,实现电机振动信号的有效提取。
1 小波阈值降噪
小波分析方法是一种灵活的局域化时频分析方法。利用多分辨分析放大特性逐步细化故障信号频谱,发挥时域频域局部化的性能,使故障特征信息明显表现出来,便于观察分析。
1.1 小波阈值降噪原理
理论分析认为,含噪信号的真实值与噪声的小波系数在小波空间内有不同分布,对含噪信号进行小波分解后,噪声主要集中在高频的小波系数中,通过设置阈值可将含噪部分去除,最后对信号重构,即达到对信号降噪的目的[10]。假设含噪的电机振动信号为s,满足:

小波阈值降噪一般步骤如图1所示。其中,最主要的是阈值和阈值函数选取,也就是本文研究的核心算法。

1.2 常用阈值选取方法
目前常用的小波降噪阈值选取方法有4种:固定阈值、无偏似然估计阈值、启发式阈值和极大值极小值阈值。但这些阈值估计方法都不是最优的,工程中应用较多的固定阈值在噪声较多时降噪效果明显,无偏似然估计对高频信息保留较多,启发式阈值与极大极小阈值在信号的高频信息较少包含噪声时比较有效[11]。因此需要找到针对不同含噪信号的最佳阈值。
2 改进阈值算法
文献[12]研究指出,电机故障信号的小波系数服从广义高斯分布,满足Bayes估计条件。
贝叶斯阈值是采用贝叶斯统计理论推导得到的[13],对于某一给定的高频信号,阈值选择为:

因为噪声对应的小波系数在每一个尺度上随机均匀分布,随着分解尺度的增加其幅值在减小,所以本文将阈值取为:

其中,j为分解尺度。随着j的增加,阈值σ减小,与改进之前相比,更符合噪声在各层的分布情况。因此,用该阈值降噪,降噪效果更好。
对式(2)的σn,采用中值估计[3]:

3 改进阈值函数
以往的小波贝叶斯阈值降噪,常选用硬阈值函数和软阈值函数,但存在固定偏差和不连续性等问题。文献[14]中提出了半软阈值函数,表达式为:

其中,δ为阈值,ω为小波系数,ω′为阈值处理后的小波系数,α是范围在(0,1)的系数。
半软阈值介于软、硬阈值方法之问,尽管避免了软硬阈值的弊端,但是其中的参数在运用中取固定值,因此仍然存在固有偏差和不连续性。针对上述问题和缺点,文献[15]提出了一种新阈值函数改进算法,并将该算法应用在指纹图像处理领域。

该算法在阈值点处连续,解决了硬阈值函数带来的振荡问题和软阈值函数带来的偏差问题,可根据参数t灵活调节阈值以适应不同噪声,但是显然,该阈值函数属于软阈值函数特性。为了克服软阈值函数的缺陷,需要将软阈值函数和硬阈值函数结合起来构造新阈值函数,故此,本文在此基础上结合文献[16]进一步改进,得到如式(9)的改进算法,并将该算法首次应用在电机振动信号处理领域。

当u取0~1之间不同值时,新阈值函数介于硬阈值函数和软阈值函数之间,这样不但克服了硬阈值函数和软阈值函数各自存在的缺陷,同时通过调节参数?琢和t使得新阈值函数相比式(8)变得更灵活。
下面对改进阈值函数进行分析。
(1)连续性


综上所述:新阈值函数是以?棕′=?棕为渐近线。
(3)偏差性

(4)阈值可变因子影响分析
当α=0,t→0时,新阈值函数为软阈值函数;t→∞,新阈值函数变为硬阈值函数;α→∞,新阈值变为硬阈值函数。所以,新阈值函数不仅具有整体连续性的特点,而且根据实际情况进行参数调节也十分灵活。
4 算法验证
若将原始信号作为标准信号s(t),则经各种降噪模型降噪的估计信号![]() 的信噪比(SNR)定义为:
的信噪比(SNR)定义为:

降噪后信号的信噪比越高,原始信号与估计信号的均方根误差越小,则估计信号越接近于真实信号,降噪效果越好。
算法验证中首先以MATLAB自带的信号为例,对其加入一定信噪比(12 dB)的高斯白噪声,并用固有Heursure、Sqtwolog、Minimaxi以及文献[13]算法和本文新阈值算法分别对其进行降噪处理,结果如图2所示。用硬阈值函数、软阈值函数、文献[15]阈值函数和本文改进阈值函数分别对其做降噪处理,结果如图3所示。


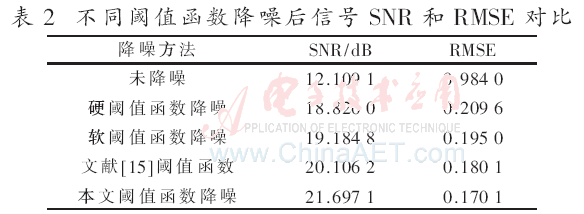
各种降噪方法性能指标如表1、表2所示。从表中可以看出,相比于其他方法,改进算法的信噪比有所提高,同时均方误差下降,降噪效果最好,所以该算法优于其他算法。

5 改进算法在振动信号降噪中的应用
数据来源于辽宁科技大学国家大学科技园电机振动实验台采集的转子不对中振动信号,采用db4小波函数。转子的转速为924 r/min,采样频率500 Hz,采集1 049个采样点,对振动信号进行5层小波包分解,采用贝叶斯新阈值,结合改进阈值函数对采样信号进行降噪处理。
如图4所示,转子不对中故障信号2倍频明显,同时在对应尖峰的恢复上,改进阈值函数结合新阈值算法降噪效果明显。利用该方法进行降噪很好地保留了尖峰和突变部分,并可以将信号高频部分和噪声引起的高频干扰有效地区分,对高频部分进行降噪处理,提高信噪比,使冲击响应特性更加突出,便于信号特征量的提取。

6 结论
在电机振动信号处理过程中,振动信号的去噪效果对电机振动信号特征提取与分析起着至关重要的作用。利用贝叶斯新阈值结合新阈值函数的新方法,针对模拟信号与实测振动信号的降噪处理,表明在振动信号降噪方面,通过设置合适的阈值结合新阈值函数能达到满意的降噪效果,既能反映振动的真实特性信息又保留了信号的高频部分特性。本文方法具有一定的使用价值。
根据模拟信号仿真结果可知,基于贝叶斯新阈值和改进阈值函数降噪算法都能够有效地提高信噪比,降低均方根误差,同时抑制高频噪声,能够恢复信号中的真实有用信号。通过实测电机振动信号处理可知,改进的降噪算法应用在电机振动信号处理中具有较好的降噪效果。
参考文献
[1] 吴光文,王昌明,包建东,等.基于自适应阈值函数的小波阈值降噪方法[J].电子与信息学报,2014,36(6):1340-1347.
[2] MALLAT S.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674-693.
[3] DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[4] 潘泉,张磊,孟晋丽,等.小波滤波方法及应用[M].北京:清华大学出版社,2005.
[5] Grace Chang,Yu Bin,Martin Vetterli.Adaptive wavelet thresholding for lmage denoising and compression[J].IEEE Trans Image Processing,2000,9:1532-1546.
[6] 刘继红,贾振红,覃锡忠,等.基于权重粒子群优化阈值的NSCT图像降噪[J].计算机工程,2012,38(10):209-211.
[7] 陈晓娟,王文婷,贾明超,等.基于小波熵自适应阈值的语音信号降噪新方法[J].计算机应用研究,2014,31(3):753-755.
[8] 闫峰.基于小波变换语音信号降噪及DSP算法实现[D].哈尔滨:哈尔滨工业大学,2008.
[9] 谢巍盛,杨根科.基于尺度噪声能量估计的自适应语音降噪算法[J].上海交通大学学报,2012,46(9):1146-1150.
[10] DONOHO D L,JOHNSTONE I M.Wavelet shrinkage:asymp-topia[J].Journal of the Royal Statistical Society,1995,57(2):301-369.
[11] DAUBECHIES I.The wavelet transform:time-frequency localization and signal analysis[J].IEEE Transactions on Information Theory 2000,36:961-1005.
[12] 陶新民,徐晶,杜宝祥,等.基于小波域广义高斯分布的轴承故障诊断方法[J].机械工程学报,2009,45(10):61-67.
[13] 敬忠良,肖钢.图像融合—理论与应用[M].北京:高等教育出版社,2007:26-27.
[14] 李迎春,孙继平,付兴建.基于小波变换的红外图像降噪[J].激光与红外,2006,36(10):988-991.
[15] 黄玉昌,侯德文.基于改进小波阈值函数的指纹图像降噪[J].计算机工程与应用,2014,50(6):179-181.
[16] 王蓓,张根耀,李智,等.基于新阈值函数的小波阈值降噪算法[J].计算机应用,2014,34(5):1499-1502.

